3.2. Строение нейтронной звезды

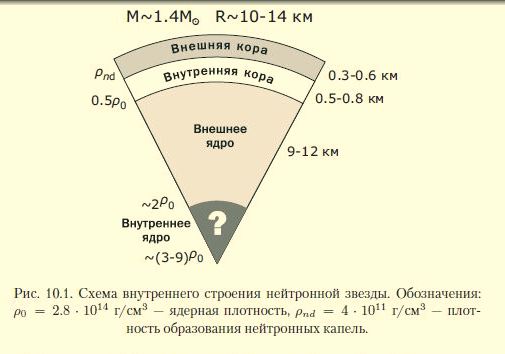
рис. 2. строение нейтронной звезды

В нейтронной звезде можно выделить четыре основные области. Первая – внешняя кора, слой толщиной 300-600м, представляющий собой кристаллическую решетку атомов (в основном, железа) и вырожденных электронов. Вторая область – внутренняя кора, слой толщиной 500-800м. Его образуют перенасыщенные нейтронами ядра, а также вырожденные электроны и нейтроны. При дальнейшем движении внутрь звезды плотность возрастает настолько, что в следующих слоях уже не могут существовать отдельные атомные ядра.

Третий слой – внешнее ядро, толщиной 9-12 км. Он представляет собой жидкость вырожденных нейтронов с малой примесью вырожденных протонов и электронов (возможно, и других частиц, например, мюонов). О свойствах этой области достоверно ничего не известно.

Еще меньше известно про внутреннее ядро. Плотности здесь могут достигать 20ρ_я. Помимо нейтронов здесь должны существовать другие частицы. Существует несколько гипотез о том, как реализуется их взаимодействие, но в целом вопрос остается открытым.

3.3. Способы наблюдения нейтронных звезд

Переходим от теории к практике – к тому, как увидеть НЗ и как измерить их параметры. Светимость НЗ в оптическом диапазоне крайне низкая, поэтому НЗ наблюдают в радио- и гамма- диапазонах, а также в рентгене.

Как было сказано выше, НЗ наблюдаются как пульсары, т.е. как источники периодически повторяющихся импульсов излучения. При перетекании вещества на НЗ (например, в двойной системе) наблюдается рентгеновское излучение, образующееся при аккреции вещества на НЗ. При полях >10¹⁰Гс НЗ светит как рентгеновский пульсар. При меньших полях вещество накапливается на поверхности, пока не происходит термоядерный взрыв. Взрыв вызывает вспышку рентгеновского излучения, поэтому такая НЗ становится вспышечным источником – барстером.

Некоторую информацию можно почерпнуть из измерений периода пульсаций. Во-первых, он увеличивается, откуда можно оценить темп потери энергии нейтронной звездой. Во-вторых, помимо монотонного роста, наблюдаются скачкообразные изменения, которые, возможно, являются следствием растрескивания коры и звездотрясений.

По задержке прихода импульсов на разных частотах можно оценить (правда, весьма грубо) расстояние до НЗ (этот эффект связан с распространением волн в космической плазме).

Важную задачу представляет собой измерение масс и размеров нейтронных звезд. Экспериментальные данные для этих величин помогли бы уточнить уравнение состояния сверхплотной материи.

Радиусы НЗ можно найти из измерений красного смещения , где – разность между регистрируемой длиной волны λ и истинной длиной волны , по формуле

где − гравитационный радиус. Это эффект, связанный с наличием сильного гравитационного поля у НЗ, соотношение для z следует из ОТО.

Массы нейтронных звезд также могут быть определены из астрономических наблюдений.

Для одиночных НЗ массу можно оценить косвенно. Зная расстояние до звезды и определив по спектру эффективную температуру T_e, из формулы для светимости

можно найти радиус, а дальше по соотношению масса-радиус определить массу. Однако это соотношение зависит от выбора уравнения состояния, поэтому такой способ оказывается неточным.

Наиболее точные результаты получаются для двойных систем. Для системы НЗ-оптическая звезда измеряют параметры орбитального движения компонентов, а из них – отношение масс компонентов. Массу оптической звезды оценивают по ее спектральному классу.

В системах НЗ-НЗ можно также измерять релятивистские эффекты: поворот оси орбиты, гравитационное красное смещение, гравитационное запаздывание импульсов, вековое уменьшение периода из-за излучения гравитационных волн. Наблюдения таких систем дают наиболее точные результаты для масс, а также позволяют проверять различные теории гравитации.

Еще одна величина, которую, возможно, можно будет аккуратно измерить в будущем – момент инерции НЗ. Измерив момент инерции и массу, можно посчитать радиус, что позволит уточнить уравнение состояния.