Тема 9. Нелинейное, динамическое, выпуклое программирование
Студент должен знать постановку задач и алгоритмы решения задач нелинейного, динамического,
выпуклого программирование и уметь применять их при решении задач линейного программирования.
Примерные тестовые задания, предлагаемые в этой теме:
1. Дана исходная задача линейного программирования:
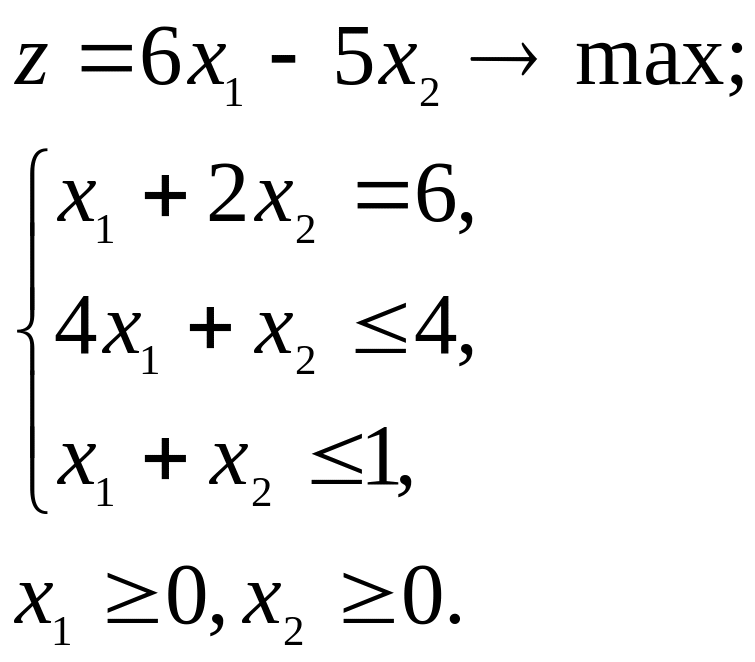
Построить двойственную задачу.
2. Пусть в исходной задаче находится минимум целевой функции. Для составления двойственной ей задачи основные ограничения должны иметь знак …
3. Пусть в исходной задаче находится максимум целевой функции. Для составления двойственной ей задачи основные ограничения должны иметь знак …
4. Дана задача линейного программирования:
Чему равно количество двойственных переменных?
5. Пусть исходная задача линейного программирования имеет оптимальное решение, что можно сказать о
решении двойственной к ней задачи?
6. Пусть целевая функция исходной задачи линейного программирования не ограничена, что в этом случае можно сказать о двойственной к ней задаче?
7. Система ограничений исходной задачи линейного программирования несовместна, что тогда можно сказать о двойственной к ней задаче?
8.
В начальном опорном плане исходной
задачи базисными переменными являются
,
.
Таблица, содержащая оптимальный план исходной задачи имеет вид:
базисные переменные |
коэф-т целевой функции |
свободные члены |
|
|
|
|
|
1 |
5 |
0 |
1 |
|
|
|
3 |
1 |
1 |
0 |
|
1 |
|
30 |
0 |
0 |
|
|
|
Назовите оптимальный план двойственной задачи.
9. В результате
решения задачи симплексным методом
получили
.
Целевая функция соответствующей двойственной задачи будет равна …
10. К какому разделу
математического программирования
относится задача: «Найти условный
экстремум функции
,
если
»?
11. Какой вид в
задаче нелинейного программирования:
«Найти условный экстремум функции
,
если
»
будет иметь функция Лагранжа? Найти
частную производную функции Лагранжа
по переменной
.
12. При решении
задачи выпуклого программирования в
стационарной точке второй дифференциал
,
следовательно, в этой точке функция
имеет…
13. При решении
задачи выпуклого программирования в
стационарной точке второй дифференциал
,
следовательно, в этой точке функция
имеет…
14. К чему сводится необходимое условие существования экстремума в задаче выпуклого программирования?
15. Что позволяет найти система уравнений:
при решении задачи выпуклого программирования методом Лагранжа?
16. При решении
задачи выпуклого программирования в
стационарной точке второй дифференциал
,
следовательно, в этой точке функция
имеет…
17. Чем позволяет воспользоваться при решении нелинейной задачи теорема Куна-Таккера для решения задачи квадратичного программирования?
18. В каком разделе математического программирования решаются задачи, в которых на все или некоторые
переменные
наложено условие целочисленности
?
20. Чему равна
дробная часть числа
?
21. Чему равна целая часть числа ?
22. Дана сеть дорог, для которой указаны расстояния между пунктами:
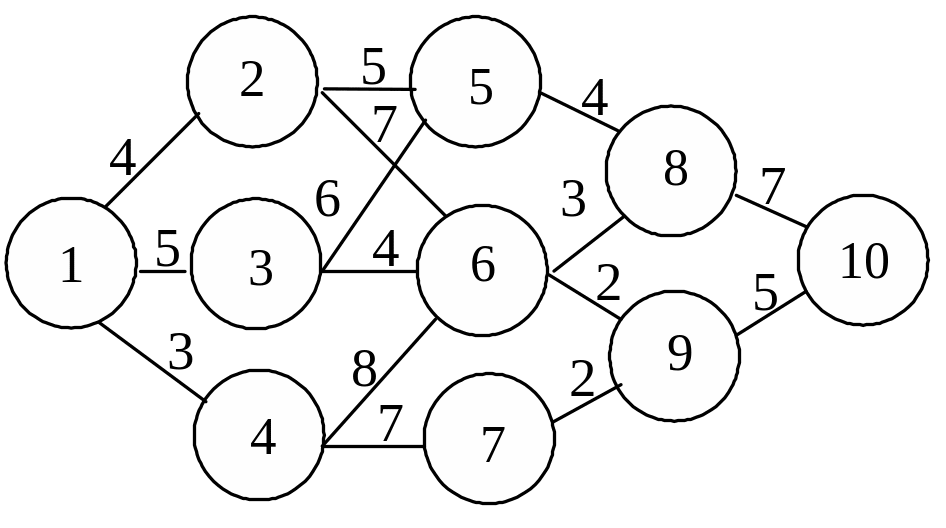
Кратчайшее расстояние из пункта 5 в пункт 10 составит …
23. Дана сеть дорог, для которой указаны расстояния между пунктами:
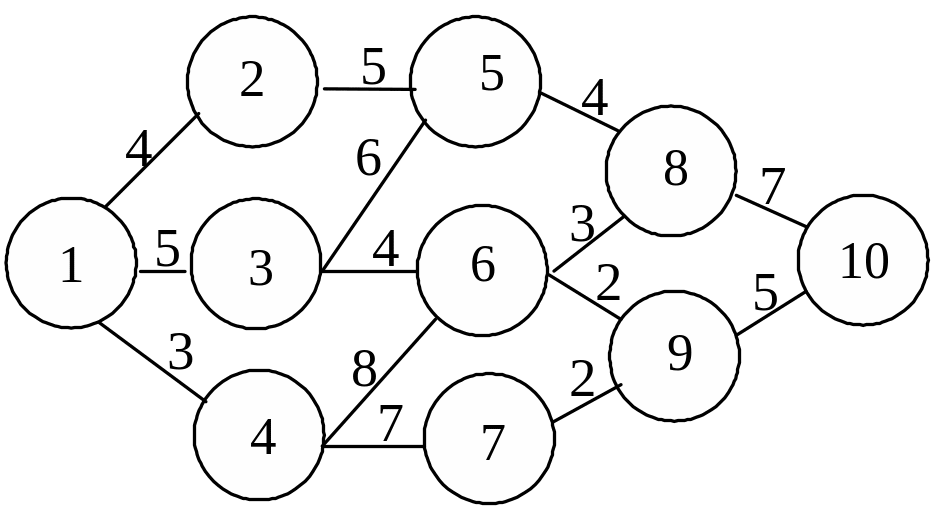
Чему
равна длина пути
?
24. Что служит признаком отсутствия целочисленного решения?
25. При решении задачи симплексным методом получили симплексную таблицу, содержащую оптимальный план.
базисные переменные |
коэф-т целевой функции |
свободные члены |
|
|
|
|
|
3 |
4 |
0 |
1 |
2 |
1 |
|
1 |
|
1 |
0 |
|
|
|
|
0 |
0 |
|
|
|
Какой вид имеет правильное отсечение для получения целочисленного плана?