Тема 4. Математическая статистика

Основные понятия по теме:

1. Неравенство Чебышева, теорема Чебышева.

2. Генеральная и выборочная совокупности.

3. Вариационный ряд и его характеристики.

4. Точечные оценки, их свойства. Интервальные оценки.

5. Метод произведений.

6. Статистическая, нулевая, простая, сложная гипотезы.

7. Ошибки первого и второго рода.

8. Статистический критерий.

9. Уровень значимости.

10. Проверка гипотез.

11. Основные понятия дисперсионного анализа.

12. Общая, факторная, остаточная, исправленная факторная дисперсии.

13. Основные понятия теории корреляции.

Применение этих понятий на практических примерах.

Примерные тестовые задания, предлагаемые в этой теме:

1. Согласно неравенству Чебышева, вероятность того, что отклонение случайной величины от ее

математического ожидания по абсолютной величине меньше положительного числа , не меньше, чем …

2. Критическая область для проверки гипотезы имеет вид: . Гипотеза будет отвергнута, если …

3. Критическая область для проверки гипотезы имеет вид: . Гипотеза будет отвергнута, если …

4. Критическая область для проверки гипотезы имеет вид: . Гипотеза будет отвергнута, если …

5. Для того, чтобы к последовательности случайных величин была применима теорема Чебышева, достаточно чтобы они …

6. Даны значения признака : 10, 5, 7, 4, 15. Чему равен ранг «10»?

7. Даны значения признака : 13, 20, 15, 14, 21. Чему равна разность рангов «20» и «21»?

8. Даны значения признаков:

	2	13	20
	7	9	8

Чему равно произведение рангов и ?

9. Если и качественные признаки, то взаимосвязь между ними можно оценить с помощью …

10. Найти внутригрупповую дисперсию по данным:

Первая группа		Вторая группа
2	1	3	2
4	7	8	3
5	2
; ;		; ;

11. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.

Проверить нулевую гипотезу о равенстве групповых средних, если , .

12. Результаты испытаний представлены в таблице:

номер испытания	уровни факторов
1	51	52	42
2	52	54	44
3	56	56	50
4	57	58	56

Общая дисперсия равна 266, факторная дисперсия 152. Найти остаточную, исправленную факторную, остаточную исправленную дисперсии.

13. Дисперсия признака вычисляется по формуле …

14. Вся совокупность объектов, характеризующая изучаемый признак, называется …

15. Часть генеральной совокупности называется …

16. Если элементы после выбора возвращаются обратно, то выборка …

17. Если выбранные элементы не возвращаются, то выборка …

18. Число отобранных значений выборки называется …

19. Наибольшей вариантой, наибольшей частотой вариационного ряда являются …

		0	1	6
	15	22	13	27

20. Статистическая оценка, которая определяется одним числом, называется …

21. Точечная оценка, математическое ожидание которой равно оцениваемому параметру, называется…

22. Объем выборки, представленной вариационным рядом равен …

		0	2
	10	20	15

23. Вариационный ряд:

	10	20	30

Является вариационным рядом …

24. Ломаная, отрезки которой соединяют точки , , …, , где — варианты выборки,

— соответствующие им частоты, называется …

25. Точечная оценка, математическое ожидание которой не равно оцениваемому параметру, называется …

26. Выборочная средняя является …

27. Выборочная дисперсия является …

28. Выборочное среднее квадратическое отклонение является …

29. Для вариационного ряда выборочное среднее , выборочная дисперсия равны …

		0	1
	5	2	3

30. Доверительный интервал для оценки математического ожидания при выборочной средней и

точности оценки имеет вид …

31. Метод произведений для расчета числовых характеристик вариационного ряда применяется, если

варианты …

32. Точечной оценкой не является …

33. Интервальной оценкой математического ожидания является …

34. В формуле для вычисления коэффициента линейной корреляции вместо «?» надо поставить …

35. Результаты измерений признаков и изображены в виде точек на корреляционном поле в виде рисунка.

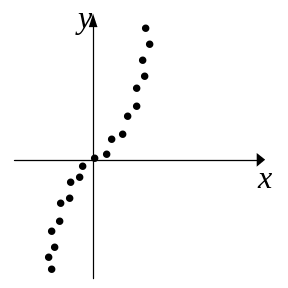
Тогда связь между признаками является …, зависимость между признаками определяется уравнением …

36. Если признаки , независимы, то коэффициент корреляции равен …

37. Коэффициент корреляции , тогда связь между признаками …

38. Если признаки и линейно зависимы, причем наблюдается обратная зависимость, то …

39. Пусть в результате измерения величины получено значение , и пусть на процесс измерения влияют случайные независимые факторы и . Тогда для оценки значимости факторов и применяют…

40. Пусть в результате измерения величины получено значение , и пусть на процесс измерения влияют случайные независимые факторы и . Пусть — дисперсия , — дисперсия , — остаточная дисперсия. Тогда для оценки значимости факторов и сравнивают …