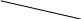Тема 3. Случайные величины. Законы распределения

Основные понятия по теме:

1. Случайная величина.

2. Дискретная и непрерывная случайная величина.

3. Закон распределения случайной величины.

4. Функция распределения случайной величины и ее свойства.

5. Плотность распределения вероятностей (дифференциальная функция распределения).

6. Числовые характеристики дискретной и непрерывной случайных величин.

7. Основные законы распределения случайных величин (биномиальное распределение,

распределение Пуассона, равномерное распределение, показательное распределение,

нормальное распределение).

8. Параметры распределений (математическое ожидание, дисперсия, среднее квадратическое отклонение).

9. Двумерные случайные величины.

10. Вероятность попадания в интервал.

Применение этих понятий на практических примерах.

Примерные тестовые задания, предлагаемые в этой теме:

1. Дискретная случайная величина имеет закон распределения:

	0,2	0,4	0,6	0,8
	0,1	0,2		0,5

Чему равна вероятность ?

2. Закон распределения дискретной случайной величины задан следующей таблицей:

	0	1	2
	0,3	0,4	0,3

Определить значение функции распределения этой случайной величины на интервале

3. Игральный кубик бросают 4 раза. Случайная величина — число выпадений 5 очков. Указать возможные значения данной случайной величины.

4. Закон распределения дискретной случайной величины задан следующей таблицей:

	– 1	0	2
	0,1	0,6	0,3

Определить математическое ожидание.

5. Определить математическое ожидание случайной величины , если известно, что .

6. Определить дисперсию случайной величины , если известно, что , .

7. Определить дисперсию случайной величины , если известно, что .

8. Двумерная дискретная величина задана законом распределения:

	1	2
0	0,1	0,3
1	0,4

Чему равна вероятность ?

9. Двумерная дискретная величина задана законом распределения:

	1	3
2	0,2	0,15
3	0,35	0,3

Определить одномерный закон распределения компоненты .

10. Функция распределения случайной величины имеет вид:

Определить плотность распределения случайной величины .

11. Дана функция распределения случайной величины

Определить вероятность того, что в результате испытания величина примет значение из интервала .

12. График функции распределения случайной величины имеет вид …

13. Плотность распределения вероятностей случайной величины имеет вид:

Математическое ожидание случайной величины определяется по формуле …

14. Плотность распределения вероятностей случайной величины имеет вид:

Дисперсия случайной величины определяется по формуле …

15. Степень разброса значений случайной величины вокруг ее математического ожидания определяет…

16. Вероятность попадания непрерывной случайной величины в интервал через вычисляется

по формуле …

17. Характеристикой среднего значения случайной величины служит …

18. Случайная величина называется распределенной по биномиальному закону, если …

19. Случайная величина называется распределенной по закону Пуассона, если …

20. Случайная величина называется равномерно распределенной на интервале , если …

21. Математическое ожидание, дисперсия непрерывной случайной величины , распределенной по

показательному закону равны …

22. Случайная величина имеет показательное распределение, если …

23. Случайная величина имеет нормальное распределение, если …

24. Случайная величина подчинена закону равномерного распределения на интервале .

Тогда ее математическое ожидание, дисперсия, среднее квадратическое отклонение равны …

25. Случайная величина подчинена закону равномерного распределения на интервале .

Тогда ее плотность распределения равна …

26. Случайная величина распределена равномерно на интервале . Дифференциальной функции распределения случайной величины соответствует график …

27. Математическое ожидание, дисперсия непрерывной случайной величины , биномиально распределенной случайной величины равны …

28. Случайная величина распределена по нормальному закону с , .

Тогда равна ...

29. Случайная величина распределена по нормальному закону с , .

Тогда равна …

30. Дифференциальная функция нормально распределенной случайной величины равна , тогда математическое ожидание и дисперсия случайной величины равны …

31. На графике изображена кривая нормального распределения вероятностей:

Математическое ожидание равно …

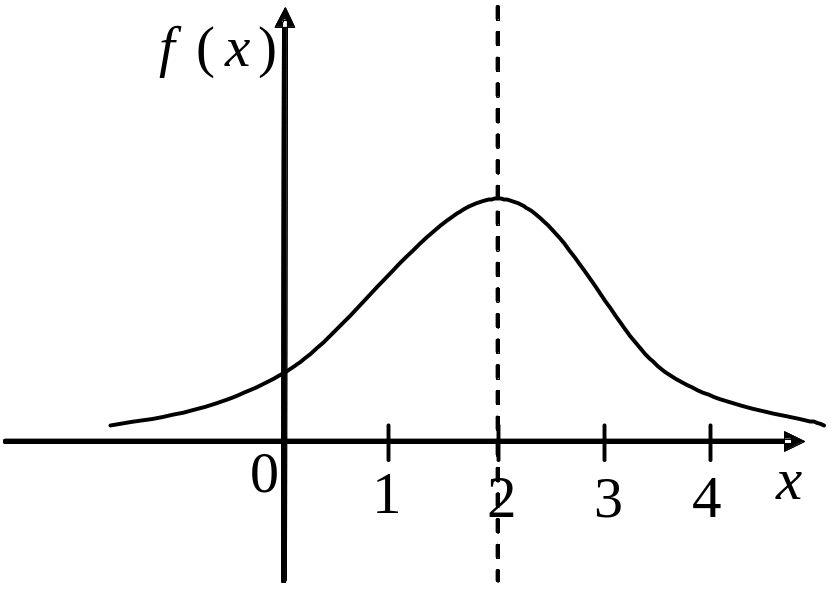
32. На рисунке изображены три нормальные кривые. Какой из нормальных кривых соответствует большее

значение ?

33. На рисунке изображены три нормальные кривые. Большему значению соответствует нормальная

кривая …