Математическая модель сау

Исходные дифференциальные уравнения системы составляются двумя методами: общим и с помощью передаточных функций.

Первый метод основан на имеющихся дифференциальных уравнениях элементов системы, записанных в операционной форме. Составляется система уравнений, которая разрешается относительно x_вых:

,

где – характеристический полином, определяющий свободное движение системы;

– полином, характеризующий влияние задающего воздействия x_з на выходную величину x_вых;

– полином, характеризующий влияние возмущающих воздействий x_f на x_вых.

Систему уравнений можно разрешить относительно ошибки, тогда

.

Допустим, САУ представлена структурной схемой (рис. 2.1).

Рис. 2.1 Структурная схема САУ

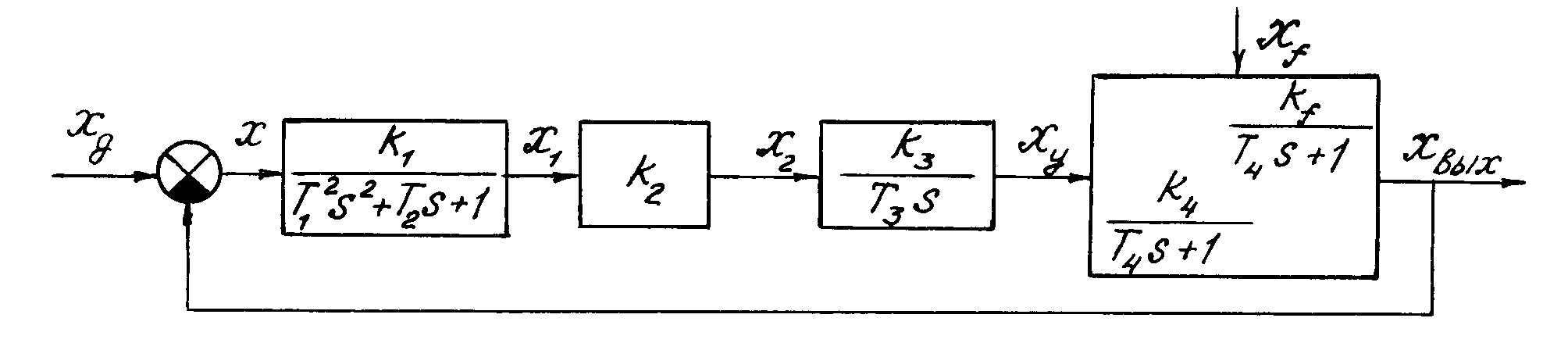
Система дифференциальных уравнений:

;

;

;

;

.

Использовав метод подстановки, разрешим систему уравнений относительно x_вых:

;

D(p) = a₀ p⁴ + a₁ p³ + a₂ p² +a₃ p + a₄;

; N(p) = c₀ p³ + c₁ p² + c₂ p.

Аналогично можно разрешить систему уравнений относительно ошибки x.

Второй метод основан на передаточных функциях системы.

Необходимо получить передаточную функцию разомкнутой системы

,

где k₁ k₂ k₃ k₄ = k_общ.

Передаточная функция управляемого объекта по возмущению

.

Подставив эти выражения в уравнение, разрешенное относительно ошибки, получим:

.

Аналогично составляем уравнения относительно x_вых:

.

Динамические характеристики САР можно получить аналитически с учетом фактических значений параметров всех звеньев или с использованием специальных программ (см. комплекс “Avtomat”).

Устойчивость систем автоматического управления

Статика предусматривает рассмотрение установившихся равновесных состояний автоматической системы при постоянных воздействиях. Исходя из статики может быть собрана принципиально работающая система. Однако более полная оценка качества управления может быть дана лишь на основе рассмотрения динамики системы. Для этого требуется наличие математической модели автоматической системы.

Анализ математической модели предусматривает оценку устойчивости и качества управления. Система, несомненно, должна быть устойчивой. Качество управления оценивают по величинам принятых показателей качества, которым должна удовлетворять автоматическая система.

В том случае, если система не удовлетворяет установленным для нее показателям качества, необходимо осуществлять ее коррекцию с помощью вспомогательных средств до тех пор, пока откорректированная система не обеспечит требуемое качество. Лишь после отладки имеет смысл переход к использованию требуемой автоматической системы.

Устойчивость — особое свойство системы, определяющее характер ее собственных движений х_с. Необходимое условие для автоматической системы — она должна быть устойчива.

Устойчивость системы — это ее свойство возвращаться в состояние установившегося равновесия после снятия возмущения, нарушившего это равновесие.

Состояние равновесия определяется видом входного воздействия и характеризуется невозмущенным движением системы. Оно описывается установившейся частью х_п решения и связано с корнями уравнения. Возмущенное движение в отклонениях от невозмущенного х_с=х-х_п представляет собой переходный процесс в автоматической системе, который определяется начальными отклонениями координат или внезапным появлением входного воздействия.

Следовательно, в аналитической форме условие устойчивости данного невозмущенного движения примет вид

lim x_с(t) → 0

t → ∞

Отсюда вытекает прямой способ исследования устойчивости системы: по найденному решению однородного дифференциального уравнения. Для устойчивой системы переходные процессы носят затухающий характер (переходная кривая стремится к установившемуся состоянию).

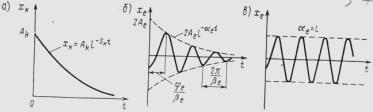
Переходные составляющие для различных корней характеристического уравнения

Однако, как было показано в предыдущем разделе, возмущенное движение линейной системы определяется корнями характеристического полинома. Cистема в таком случае будет устойчивой, если все вещественные корни s_h характеристического полинома отрицательны (первая сумма), а у комплексных отрицательна действительная часть а_г (вторая сумма). В этом случае кривые переходных процессов будут стремиться к оси абсцисс. Если вещественный корень Sk или действительная часть пары комплексных корней а_г положительны, то система неустойчива вследствие расходящегося переходного процесса. Случай s_h = 0 или ос; = 0 соответствует границе устойчивости соответственно апериодической или колебательной.

Д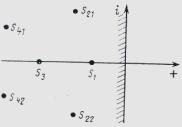 ля удобства анализа корни характеристического уравнения наносят на комплексную плоскость. Система устойчива, если все корни лежат в левой полуплоскости. Следовательно, левая полуплоскость определяет область устойчивости. Границей области устойчивости является на плоскости корней характеристического уравнения мнимая ось. Принято область устойчивости отштриховывать по ее границе слева при движении от минус бесконечности к бесконечности.

Плоскость корней характеристического уравнения

Критерии устойчивости. Специальные условия, выполнение которых позволяет обеспечивать устойчивость системы, называются критериями устойчивости. В отличие от непосредственного решения характеристического уравнения критерии устойчивости позволяют осуществлять анализ причин неустойчивости и намечать пути ее устранения.

Различают алгебраические и частотные критерии устойчивости. Первые (Рауса, Гурвица) нетрудно проверить при ручном счете для системы невысокого порядка. Частотные критерии устойчивости (Михайлова, Найквиста) могут оказаться более предпочтительными для системы высоких порядков.

Критерий устойчивости Гурвица. Автоматическая система, имеющая характеристическое уравнение

a₀λⁿ+ a₁λ^n-1+…+a_n=0. (6.2)

где а₀ > 0, устойчива при условии

Δ_i>0.

Определители Гурвица Δ_i находятся из матрицы коэффициентов

,

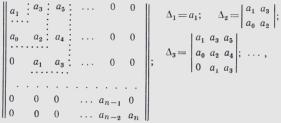в которой по главной диагонали выписываются все коэффициенты, начиная со второго. Столбцы матрицы заполняются коэффициентами вверх от диагонали по возрастающим индексам, а вниз по убывающим. При индексе больше п и меньше нуля вместо коэффициентов записываются нули. Определители Δ_i выбираются из матрицы, состоящими из i строк и столбцов. Последний определитель Δ_n включает в себя всю матрицу и выражается через Δ_n-1:

Δ_n-1=a_nΔ_n-1.

Условие, соответствующее апериодической границе устойчивости, принимает вид

а_n=0,

а колебательной границе устойчивости

Δ_n-1=0

Анализ определителей Гурвица позволяете каждом частном случае условия устойчивости упростить. Так, для системы первого и второго порядков условие устойчивости а_i > 0; для системы третьего порядка a_i > 0, Δ₂ > 0; для системы четвертого порядка а_i > 0, Δ₃ > 0; для системы пятого порядка а_i > 0, Δ₄ > 0; Δ₂ > 0; для системы шестого порядка а_i > 0, Δ₅ > 0, Δ₃ > 0 и т. п.

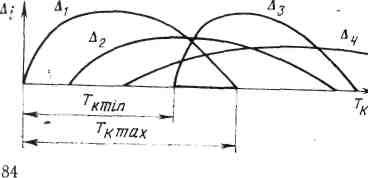
Обеспечение устойчивости за счет изменения какого-либо параметра T_k осуществляется на основе анализа зависимости Δ_i = Δ_i (T_k). Параметр T_k должен лежать в пределах T_{k min} ≤ T_k ≤ T_{k max}, обеспечивающих Δ_i > 0. Графическая интерпретация этого способа показана на рис. 6.3.

Критерий устойчивости Михайлова. Автоматическая система при характеристическом полиноме D (λ) степени п будет устойчивой, если полное приращение фазы характеристического комплекса D (iω) при изменении ω от 0 до ∞ составит п .

Характеристический комплекс D (iω) получают из характеристического полинома

заменой λ = iω:

где ψ(ω) — фаза или аргумент комплекса;

Определение зоны устойчивости

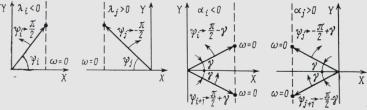
На комплексной плоскости X, Y характеристический комплекс представляется вектором с амплитудой D(ω) и фазой ψ(ω). Общая фаза ψ(ω)складывается из фаз векторов каждого сомножителя (iω – λ_i). Фаза ψ_i при вещественном отрицательном корне λ_i составит , а положительном - . Фаза ψ_i+ψ_i+1 при отрицательной действительной части α_i составит 2 , а положительной -2 . Следовательно, если все п корней лежат в левой полуплоскости, то общая фаза вектора D (ω) согласно (6.9) при изменении ω от 0 до ∞ составит п .

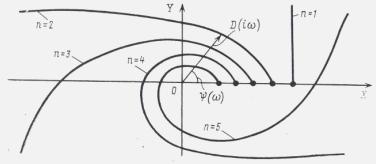
Для исследования устойчивости на комплексной плоскости строят годограф Михайлова, т. е. кривую, которую прочертит конец вектора D (iω). Если система устойчива, то кривая Михайлова плавно пройдет п квадрантов, уходя в последнем в бесконечность. Если кривая Михайлова пройдет меньше чем п квадрантов (больше п она пройти не может), то система неустойчива. Проход кривой Михайлова через нулевую точку осей координат соответствует границе устойчивости. Годографы Михайлова устойчивых систем различных порядков.

Построение кривой Михайлова обычно осуществляют, находя X (ω) = а_п - а_n-2 ω ² + ... и Y (ω) = а_п-1 – a_n-3 ω³ + ... непосредственно или путем чередования корней полиномов X (ω) и Y (ω), так как кривая Михайлова должна для устойчивой системы поочередно пересечь оси абсцисс и ординат.

Критерий устойчивости Найквиста. Критерий Найквиста характеризует устойчивость системы по годографу частотой передаточной функции разомкнутой системы, что проще и может быть осуществлено экспериментально.

При использовании критерия Найквиста следует проанализировать характер корней знаменателя передаточной функции разомкнутой системы W(s)=G(s)/Q(s), где G(s) и (s). Следует иметь в виду, что D(s)=Q(s)+G(s) в соответствии с (5.78). Характер корней полинома Q(s) отражает наличие устойчивости или неустойчивости в разомкнутом состоянии системы.

Наиболее характерным является случай отсутствия корней знаменателя Q(s) передаточной функции разомкнутой системы W(s) в правой полуплоскости. Для этого случая критерий Найквиста трактуется следующим образом: устойчивость обеспечивается, если годограф частотной передаточной функции разомкнутой системы W(s) не охватывает точку с координатами (-1, i0). На рисунке показана графическая интерпретация этого критерия.

Наличие в знаменателе частотной передаточной функции разомкнутой системы нулевых корней по их числу соответствует степени астатизма системы. В этом случае критерий Найквиста формулируется аналогично. Лишь сам годограф в начальный момент отличается от годографа статической системы.

Приращение фазы при изменении ω оt 0 до ∞

Годографы Михайлова

Годографы частотной передаточной функции разомкнутой системы: а. б — устойчивой; в — на границе устойчивости; г — неустойчивой

Если полином Q(s) содержит чисто мнимые корни с нулевой действительной частью (±iβ), что соответствует колебательной границе устойчивости разомкнутой системы, то критерий Найквиста в целом и здесь формулируется аналогично. На плоскости годографа при этом появляется разрыв характеристики W(iω), аргумент которой тогда получит приращение — π (полуокружность в направлении по часовой стрелке), а модуль будет стремиться к бесконечности.

Наконец, неустойчивая система в разомкнутом состоянии (k корней в правой полуплоскости у полинома Q(s)) может быть устойчивой в замкнутом. При этом критерий устойчивости Найквиста несколько видоизменяется: для устойчивой системы в замкнутом состоянии годограф частотной передаточной функции разомкнутой системы должен охватить точку (—1, i0) k раз, т. е. по числу корней в правой полуплоскости знаменателя частотной передаточной функции разомкнутой системы. На рисунке показаны случаи устойчивости системы соответственно при к = 1 и k = 2. В первом случае точка (—1, i0) охвачена один раз, во втором — два. При других значениях к годографы будут соответствовать неустойчивым системам (охват точки (—1, i0), что легко представить, если достроить ветвь для -∞ ≤ ω ≤ 0.