Варіант 1.

ТЕМА 1. Простір елементарних подій. Класичне означення ймовірності.

1 Одночасно навмання підкидають два гральних кубика та спостерігають за наступними подіями А=”сума очок, що випали на двох кубиках дорівнює 7”, В=”сума очок, що випали на двох кубиках дорівнює 9”. Яка подія більш ймовірна А чи В?

ТЕМА 2. Умовні ймовірності. Формула повної ймовірності.

Формули Байеса.

2. У одній зі студентських груп 25 дівчат та 5 хлопців. До практичного заняття з теорії ймовірностей не підготувалися 3 дівчат та 3 хлопця. Навмання опитаний студент виявився непідготовленим до заняття.

А) Яка ймовірність цієї події?

Б) Якщо , навмання опитаний студент виявився непідготовленим до заняття.

яка ймовірність, що він хлопець?

ТЕМА 3. Повторні незалежні випробування. Формула Бернуллі.

3. Оптова фірма постачає товар у 8 магазинів, від кожного з яких заявка на черговий день приходить з ймовірністю 0,75. Знайти найімовірніше число заявок у день для цієї оптової фірми та ймовірність одержання такого числа заявок.

ТЕМА 4. Дискретні випадкові величини. Числові характеристики.

Функція розподілу.

4. За даним законом розподілу дискретної випадкової величини , яка представляє суму виграшу в грн.

	0,5	1	1,5	2
	0,13				0,05

обчислити:

1. математичне сподівання (виграшу);

2. дисперсію і середнє квадратичне відхилення (виграшу);

3. функцію розподілу даної дискретної випадкової величини (виграшу) та побудувати її графік.

Тема 5. Абсолютно неперервні випадкові величини. Числові характеристики. Функція розподілу. Ймовірність потрапляння у певний проміжок.

Випадкова величина задана інтегральною функцією . Визначити:

1. диференціальну функцію 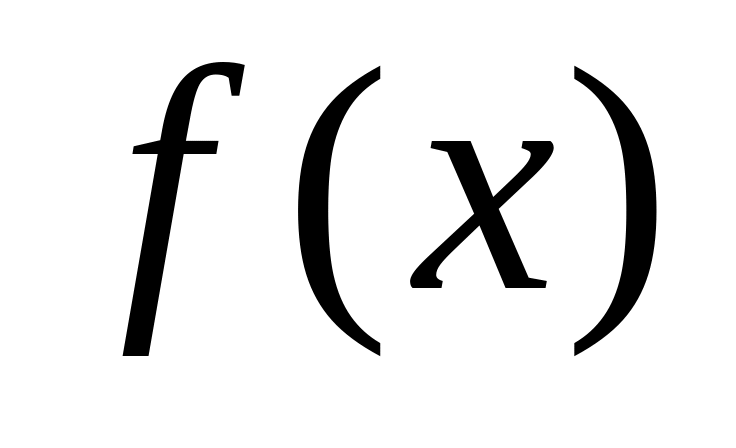(щільність розподілу);

2. математичне сподівання і дисперсію ;

3. ймовірність того, що прийме значення в інтервалі ;

4. побудувати графіки функцій і .

Тема 6. Нормальний розподіл абсолютно неперервної випадкової величини.

Визначити ймовірність того, що нормально розподілена випадкова величина - величина щоденних грошевих надходжень у день для деякого банку (у тис. грн) прийме значення, що належить інтервалу , якщо відомі математичне сподівання (у тис. грн) і середнє квадратичне відхилення .

Тема 7. Статистичний розподіл вибірки. Перевірка гіпотези про нормальний розподіл за крітерієм Пірсона. За даним статистичним розподілом вибірки визначити:

1. вибіркову середню;

2. вибіркову дисперсію;

3. вибіркове середнє квадратичне відхиленя;

4. побудувати полігон та гістограму

5. перевірити гіпотезу про нормальний розподіл за крітерієм Пірсона.

Тема 8. Кореляційна залежність випадкових величин. Вибіркове рівняння регресії. За даною таблицею – кореляційною, знайти вибіркове рівняння регресії

,

де – величина витрат на рекламу (у сот. грн.) на тиждень, – величина прибутку (у тис. грн.) на тиждень. Намалювати діаграму розсіювання і пряму регресії. Зробити прогноз відносно того, який буде прибуток (у тис. грн.) на тиждень, якщо витрати на рекламу стануть 25 (у сот. грн.) на тиждень.

Контрольні питання:

1.Повторні випробування. Формула Бернуллі. Приклад застосування.

2. Статистичний розподіл вибірки. Полігон та гістограма. Вибіркова середня; вибіркова дисперсія

Варіант 2.