4 3 2 1 0 ← Разряды
31 = k4 k3 k2 1 1N = k4·N4 + k3·N3 + k2·N2 + N1 + N0
= k·N2 + N + 1
для
(из первых трех слагаемых вынесли общий
множитель
).
Решение:
Итак, нужно найти все целые числа
,
такие что
(**)
где – целое неотрицательное число (0, 1, 2, …).
Сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа.
Из формулы (**) получаем
,
так что задача сводится к тому, чтобы
найти все делители
числа 30 и отобрать только те из них, для
которых уравнение (**) разрешимо при
целом
,
то есть,
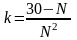– целое число.Выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30.
Из всех этих делителей только для 2, 3, 5 и 30 значение – целое число (оно равно соответственно 7, 3, 1 и 0).
Таким образом, верный ответ – 2, 3, 5, 30.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Задача № 1
Вариант №1
Как представлено число 8310 в двоичной системе счисления?
1) 10010112
2) 11001012
3) 10100112
4) 1010012
Вариант №2
Сколько единиц в двоичной записи числа 195?
1) 5
2) 2
3) 3
4) 4
Вариант №3
Сколько единиц в двоичной записи числа 173?
1) 7
2) 5
3) 6
4) 4
Вариант №4
Как представлено число 25 в двоичной системе счисления?
1) 10012
2) 110012
3) 100112
4) 110102
Вариант №5
Как представлено число 82 в двоичной системе счисления?
1) 10100102
2) 10100112
3) 1001012
4) 10001002
Вариант №6
Как представлено число 263 в восьмеричной системе счисления?
1) 3018
2) 6508
3) 4078
4) 7778
Вариант №7
Как записывается число 5678 в двоичной системе счисления?
1) 10111012
2) 1001101112
3) 1011101112
4) 111101112
Вариант №8
Как записывается число A8716 в восьмеричной системе счисления?
1) 4358
2) 15778
3) 52078
4) 64008
Вариант №9
Как записывается число 7548 в шестнадцатеричной системе счисления?
1) 73816
2) 1A416
3) 1EC16
4) A5616
Вариант №10
Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-128)?
1) 1
2) 2
3) 3
4) 4
Вариант №11
Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-35)?
1) 3
2) 4
3) 5
4) 6
Вариант №12
Дано:
,
.
Какое из чисел С, записанных в двоичной
системе счисления, удовлетворяет
неравенству
?
1) 10011010
2) 10011110
3) 10011111
4) 11011110
Вариант №13
Дано:
,
.
Какое из чисел С, записанных в двоичной
системе счисления, удовлетворяет
неравенству
?
1) 11111001
2) 11011000
3) 11110111
4) 11111000
Вариант №14
Дано:
,
.
Какое из чисел С, записанных в двоичной
системе счисления, удовлетворяет
неравенству
?
1) 11011010
2) 11111110
3) 11011110
4) 11011111
Вариант №15
Дано:
,
.
Какое из чисел С, записанных в двоичной
системе счисления, удовлетворяет
неравенству
?
1) 11101010
2) 11101110
3) 11101011
4) 11101100
Вариант №16
Дано:
,
.
Какое из чисел С, записанных в двоичной
системе счисления, удовлетворяет
неравенству
?
1) 11101010
2) 11101000
3) 11101011
4) 11101100
Вариант №17
Дано: а=D716, b=3318. Какое из чисел c, записанных в двоичной системе, отвечает условию a<c<b?
1) 11011001
2) 11011100
3) 11010111
4) 11011000
Вариант №18
Дано:
,
.
Какое из чисел С, записанных в двоичной
системе счисления, удовлетворяет
неравенству
?
1) 11010011
2) 11001110
3) 11001010
4) 11001100
Вариант №19
Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?
1) 10011010
2) 10011110
3) 10011111
4) 11011110
Вариант №20
Как представлено число 18910 в двоичной системе счисления?
1) 10010112
2) 11001012
3) 10100112
4) 101111012
Задача № 2
Вариант №1
Вычислите сумму чисел x и y, при x = A616, y = 758. Результат представьте в двоичной системе счисления.
1) 110110112
2) 111100012
3) 111000112
4) 100100112
Вариант №2
Значение выражения 1016 + 108 • 102 в двоичной системе счисления равно
1) 10102
2) 110102
3) 1000002
4) 1100002
Вариант №3
Вычислите сумму двоичных чисел x и y, если x = 10101012 и y = 10100112
1) 101000102
2) 101010002
3) 101001002
4) 101110002
Вариант №4
Вычислите значение суммы 102 + 108 +1016 в двоичной системе счисления.
1) 101000102
2) 111102
3) 110102
4) 101002
Вариант №5
Вычислите сумму чисел x и y, при x = 2718, y = 111101002. Результат представьте в шестнадцатеричной системе счисления.
1) 15116
2) 1AD16
3) 41216
4) 10B16
Вариант №6
Вычислите сумму чисел x и y, при x = A116, y = 11012. Результат представьте в десятичной системе счисления.
1) 204
2) 152
3) 183
4) 174
Вариант №7
Вычислите сумму чисел x и y, при x = 568, y = 11010012. Результат представьте в двоичной системе счисления.
1) 111101112
2) 100101112
3) 10001112
4) 110011002
Вариант №8
Вычислите сумму чисел x и y, при x = 5A16, y = 10101112. Результат представьте в восьмеричной системе счисления.
1) 1518
2) 2618
3) 4338
4) 7028
Вариант №9
Вычислите сумму чисел x и y, при x = 1278, y = 100101112. Результат представьте в десятичной системе счисления.
1) 214
2) 238
3) 183
4) 313
Вариант №10
Вычислите A8116 + 37716. Результат представьте в той же системе счисления.
1) 21B16
2) DF816
3) C9216
4) F4616
Вариант №11
Чему равна разность чисел 10116 и 1101112?
1) 3128
2) 128
3) 3216
4) 6416
Вариант №12
Чему равна разность чисел 1248 и 5216?
1) 112
2) 102
3) 1002
4) 1102
Вариант №13
Чему равна сумма чисел 278 и 3416?
1) 1138
2) 638
3) 5116
4) 1100112
Вариант №14
Чему равна сумма чисел 438 и 5616?
1) 7916
2) A316
3) 1258
4) 10101012
Вариант №15
Чему равна сумма чисел 438 и 5616?
1) 1218
2) 1718
3) 6916
4) 10000012
Вариант №16
Вычислите сумму чисел X и Y, если X=1101112 Y=1358. Результат представьте в двоичном виде.
1) 110101002
2) 101001002
3) 100100112
4) 100101002
Вариант №17
Вычислите сумму чисел x и y, при x = B816, y = 778. Результат представьте в двоичной системе счисления.
1) 110110112
2) 111100012
3) 111101112
4) 100100112
Вариант №18
Вычислите сумму чисел x и y, при x = F616, y = 358. Результат представьте в двоичной системе счисления.
1) 110110112
2) 111100012
3) 111000112
4) 1000100112
Вариант №19
Чему равна сумма чисел 538 и 6616?
1) 1278
2) 3728
3) 6916
4) 100100012
Вариант №20
Чему равна разность чисел 110116 и 11011112?
1) 3128
2) 1228
3) 32A16
4) 117016
Задача № 3
Вариант №1
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Вариант №2
В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
Вариант №3
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.
Вариант №4
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Вариант №5
В системе счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.
Вариант №6
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
Вариант №7
В системе счисления с некоторым основанием число десятичное 25 записывается как 100. Найдите это основание.
Вариант №8
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на 3.
Вариант №9
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22?
Вариант №10
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в четверичной системе счисления оканчивается на 31?
Вариант №11
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?
Вариант №12
Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.
Вариант №13
Укажите, сколько всего раз встречается цифра 1 в записи чисел 12, 13, 14, …, 31 в системе счисления с основанием 5.
Вариант №14
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 1.
Вариант №15
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 63 оканчивается на 23.
Вариант №16
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11.
Вариант №17
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Вариант №18
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Вариант №19
В системе счисления с некоторым основанием число десятичное 129 записывается как 1004. Найдите это основание.
Вариант №20
Укажите, сколько всего раз встречается цифра 2 в записи чисел 10,11,12, , …, 17 в системе счисления с основанием 5.
Задача № 4
Переведите данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Вариант №1
а) 860(10);
б) 785(10);
в) 149,375(10);
г) 953,25(10);
д) 228,79(10).
Вариант №2
а) 250(10);
б) 757(10);
в) 711,25(10);
г) 914,625(10);
д) 261,78(10).
Вариант №3
а) 759(10);
б) 265(10);
в) 79,4375(10);
г) 360,25(10);
д) 240,25(10).
Вариант №4
а) 216(10);
б) 336(10);
в) 741,125(10);
г) 712,375(10);
д) 184,14((10).
Вариант №5
а)530(10);
б) 265(10);
в) 597,25(10);
г) 300,375(10);
д) 75,57(10).
Вариант №6
а) 945(10);
б) 85(10);
в) 444,125(10);
г) 989,375(10);
д) 237,73(10).
Вариант №7
а) 287(10);
б) 220 (10);
в) 332,1875(10);
г) 652,625(10);
д) 315,21(10).
Вариант №8
а) 485(10);
б) 970 (10);
в) 426,375(10);
г) 725,625(10);
д) 169,93(10).
Вариант №9
а) 639(10);
б) 485(10);
в) 581,25(10);
г) 673,5(10);
д) 296,33(10).
Вариант №10
а) 618(10);
б) 556(10);
в) 129,25(10);
г) 928,25(10);
д) 155,45(10).
Вариант №11
а) 772(10);
б) 71(10);
в) 284,375(10);
г) 876,5(10);
д) 281,86(10).
Вариант №12
а) 233(10);
б) 243(10);
в) 830,375(10);
г) 212,5(10);
д) 58,89(10).
Вариант №13
а) 218(10);
б) 767(10);
в) 894,5(10);
г) 667,125(10);
д) 3,67(10).
Вариант №14
а) 898(10);
б) 751(10);
в) 327,375(10);
г) 256,625(10);
д) 184,4(10).
Вариант №15
а) 557 (10);
б) 730 (10);
в) 494,25 (10);
г) 737,625 (10);
д) 165,37 (10).
Вариант №16
а) 737 (10);
6) 92 (10);
в) 934,25 (10);
г) 413,5625 (10);
д) 100,94 (10).
Вариант №17
a) 575 (10);
б) 748 (10);
в) 933,5 (10);
г) 1005,375 (10);
д) 270,44 (10).
Вариант №18
а) 563 (10);
б) 130 (10);
в) 892,5 (10);
г) 619,25 (10);
д) 198,05 (10).
Вариант №19
а) 453 (10);
б) 481 (10);
в) 461,25 (10);
г) 667,25(10);
д) 305,88 (10).
Вариант №20
а) 949 (10);
б) 763 (10);
в) 994,125 (10);
г) 523,25 (10);
д) 203,82 (10).
Задача № 5
Переведите данное число в десятичную систему счисления.
Вариант №1
а) 1001010(2);
б) 1100111(2);
в) 110101101,00011(2);
г) 111111100,0001(2);
д) 775,11(8);
е) 294,3(16).
Вариант №2
а) 1111000(2);
б) 1111000000(2);
в) 111101100,01101(2);
г) 100111100,1101(2);
д) 1233,5(8);
е) 2B3,F4(I6).
Вариант №3
а) 1001101(2);
б) 10001000(2);
в) 100111001,01(2);
г) 1111010000,001(2);
д) 1461,15(8);
е) 9D,A(16)
Вариант №4
а) 1100000110(2);
б) 1100010(2);
в) 1011010,001(2);
г) 10101000,001(2);
д) 1537,22(8);
е) 2D9,8(16) .
Вариант №5
а) 101000111(2);
б) 110001001(2);
в) 1001101010,01(2);
г) 1011110100,01(2);
д) 1317,75(8);
е) 2F4,0С(16) .
Вариант №6
а) 110001111(2);
б) 111010001(2);
в) 100110101,001(2);
г) 10000010,01011(2);
д) 176,5(8);
е) 3D2,04(16) .
Вариант №7
а) 10101000(2);
б) 1101100(2);
в) 10000010000,01001(2);
г) 1110010100,001(2);
д) 1714,2(8); е) DD,3(16) .
Вариант №8
а) 10101000(2);
б) 101111110(2);
в) 1010101,101(2);
г) 1111001110,01(2);
д) 721,2(8);
е) 3С9,8(16) .
Вариант №9
а) 1011000011(2);
б) 100010111(2);
в) 1100101101,1(2);
г) 1000000000,01(2);
д) 1046,4(8);
е) 388,64(16) .
Вариант №10
а) 1000001111(2);
б) 1010000110(2);
в) 101100110,011011(2);
г) 100100110,101011(2);
д) 10232,2(8);
е) 53,9(16).
Вариант №11
а) 1001101111(2);
б) 1000001110(2);
в) 111110011,011(2);
г) 11010101,1001(2);
д) 1634,5(8);
е) C2,3(16).
Вариант №12
а) 1111100010(2);
б) 1000011110(2);
в) 101100001,011101(2);
г) 1001111001,1(2);
д) 1071,54(8);
е) 18B,0C(16).
Вариант №13
а) 101110100(2);
б) 1111101101(2);
в) 1110100001,01(2);
г) 1011111010,0001(2);
д) 744,12(8);
е) 1ЕЕ,С(16).
Вариант №14
а) 101001101 (2);
б) 1110111100 (2);
в) 10000001000,001 (2);
г) 1000110110,11011 (2);
д) 147,56 (8);
е) 1СА,3 (16).
Вариант №15
а) 1110000010 (2);
6) 1000100 (2);
в) 110000100,001 (2);
г) 1001011111,00011(2);
д) 665,42 (8);
е) 246,18(,6).
Вариант №16
а) 1010000 (2);
б) 10010000 (2);
в) 1111010000,01 (2);
г) 101000011,01 (2);
д) 1004,1 (8);
е) 103,8С (16).
Вариант №17
а) 11100001 (2);
б) 101110111 (2);
в) 1011110010,0001 (2);
г) 1100010101,010101(2);
д) 533,2 (8);
е) 32,22 (16).
Вариант №18
а) 111001010 (2);
б) 1101110001 (2);
в) 1001010100,10001 (2);
г) 111111110,11001(2);
д) 1634,35 (8);
е)6В,А (16).
Вариант №19
а) 1110001111 (2);
б) 100011011 (2);
в) 1001100101,1001 (2);
г) 1001001,011 (2);
д) 335,7 (8);
е) 14C,A (16).
Вариант №20
а) 1100010010 (2);
б) 10011011 (2);
в) 1111000001,01 (2);
г) 10110111,01 (2);
д) 416,1(в>; е) 215,7 (16).
Задача № 6
Выполните арифметические действия.
Вариант №1
1.
1101100000(2) + 10110110(2);
101110111(2) + 1000100001(2);
1001000111,01(2) + 100001101,101(2);
271,34(8) + 1566,2(8);
65,2(16) + ЗСА,8(16).
2.
1011001001(2) -1000111011(2);
1110000110(2) -101111101(2);
101010000,10111(2) -11001100,01(2);
731,6(8) - 622,6(8);
22D,l(l6) -123,8(16).
3.
1011001(2) х 1011011(2);
723,l(8) х 50,2(8) ;
69,4(16) х А,В(16).