21. Логическое выражение (формула). Таблица истинности. Старшинство операций

Логическое выражение (логическая формула) — это простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций (связок). Имеются три основных логических операции: отрицание, конъюнкция (логическое умножение) и дизъюнкция (логическое сло­ жение).

Отрицание обозначается в математической логике знаком «¬» и читается как НЕ. Это одноместная операция. Например, запись ¬ (x = у) читается следующим образом: НЕ (x равно у), т.е. значение будет истинным, если х не равно у, и ложным, если x равно у. Отрицание изменяет значение логической величины на противоположное.

Конъюнкция обозначается знаком & и читается как И. Это двух­ местная операция. Например, запись (х> 0) & (х< 1) означает, что данная логическая формула примет значение ИСТИНА, если x ϵ [0, 1], и значение ЛОЖЬ — в противном случае. Следовательно, результатом конъюнкции является ИСТИНА, если истинны оба операнда.

Дизъюнкция обозначается знаком v, который читается как ИЛИ. Например, запись (x = 0) v (x = 1) означает, что формула принимает истинное значение, если х — двоичная цифра (0 или 1). Следовательно, результатом дизъюнкции является ИСТИНА, если хотя бы один операнд имеет значение ИСТИНА.

Таблица истинности:

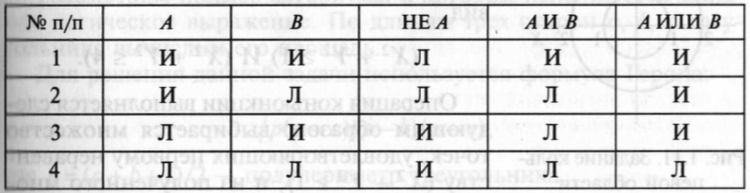
Последовательность выполнения операций в логических выражениях определяется старшинством операций: отрицание, конъюнкция, дизъюнкция. Кроме того, порядок выполнения операции в логических формулах можно менять с помощью скобок. (А И В) ИЛИ (НЕ А И В) ИЛИ (НЕ А И НЕ В).

В Паскале логические значения обозначаются служебными ело вами False (F) и True (Т), а идентификатор логического типа Boolean.

Логические операции на языке Паскаль называются: Not — отрицание, And — логическое умножение (конъюнкция); Or — логическое cложение (дизъюнкция). Кроме них в ТурбоПаскале имеется операция «Исключающее ИЛИ», обозначаемая служебным словом Хог. Это двухместная операция, которая в результате дает значение ИСТИНА, если оба операнда имеют разные логические значения.

22. Структура программы на языке Паскаль. Основные типы данных. Стандартные математические функции языка Турбо Паскаль. Правила записи арифметических выражений.

По определению стандартного языка Паскаль программа состоит из заголовка и тела (блока), в конце которого следует точка — признак конца программы. В свою очередь, блок содержит разделы описаний и раздел операторов:

Program <имя программы>;

Label <раздел меток>;

Const <раздел констант>;

Туре <раздел типов>;

Var <раздел переменных>;

Procedure (Function) <раздел подпрограмм>;

Begin <раздел операторов>

End.

Раздел операторов имеется в любой программе и является основным. Разделы описаний могут не все содержаться в каждой программе.

Основные типы данных:

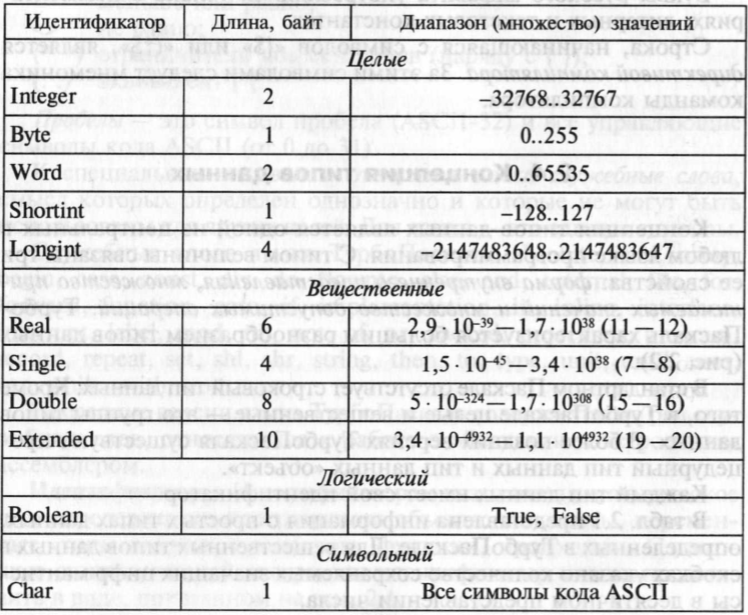
Стандартные математические функции языка Турбо Паскаль:

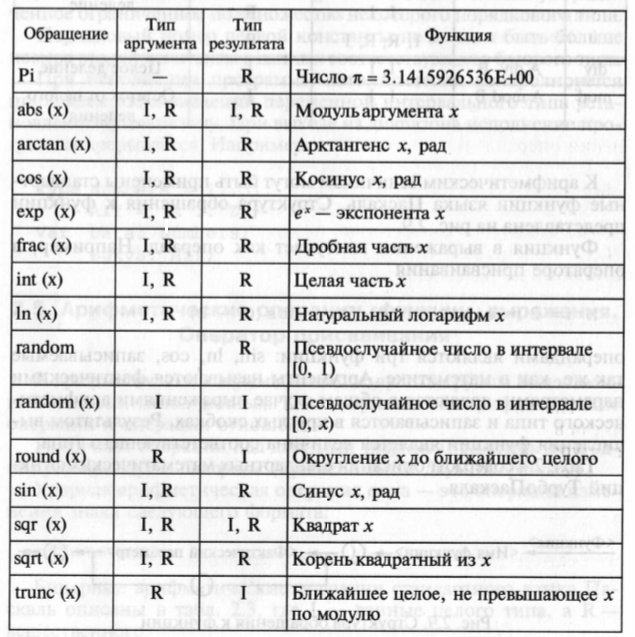
В Паскале нет операции или стандартной функции возведения числа в произвольную степень. Для вычисления х^у рекомендуется поступать следующим образом:

• если у — целое значение, следует использовать умножение, например: х³ → х * х * х. Для больших степеней следует использовать умножение в цикле;

• если у — вещественное значение, используется следующая математическая формула: х^у = е^уln(х), запись которой на Паскале имеет вид: exp (Y * In(х)).

Очевидно, что при вещественном типе у недопустимо нулевое или отрицательное значение х. Для у целого типа такого ограничения нет. Например, формула 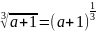, записанная на Паскале будем иметь вид ехр (1/3 * In(А + 1)).

Для верной записи арифметических выражений следует соблюдать правила:

1. Все символы писать в строку, т.е. на одном уровне. Проставлять все знаки операций, не пропуская знак «*».

2. Не допускать записи двух знаков операций подряд, т. е. нельзя писать А + -В, следует писать А + (-В).

3. Операции с более высоким приоритетом выполняют раньше операций с меньшим приоритетом. Порядок убывания приоритетов операций следующий:

• вычисление функции;

• унарная операция смены знака (-);

• *, /, div, mod;

• +, -

4. Несколько записанных подряд операций с одинаковым приоритетом выполняют последовательно слева направо.

5. Часть выражения, заключенная в скобки, вычисляется в первую очередь. (Например, в выражении (А + В) * (С - D) умножение производится после сложения и вычитания.)

6. Не следует записывать выражения, не имеющие математического смысла, например: деление на нуль, логарифм отрицательного числа и т.п.

23. Программирование ветвящихся алгоритмов

Алгоритмическая структура ветвления программируется в Паскале с помощью условного оператора, имеющего вид:

If <Условие> Then <Оператор 1> Else <Оператор 2>.

Кроме того, возможно использование неполной формы условного оператора:

If <Условие> Then <Оператор>.

Условием в условном операторе является логическое выражение, которое вычисляется в первую очередь. Если его значение равно True, то будет выполняться «Оператор 1> (после Then), если же его значение равно False, будет выполняться Оператор 2> (после Else) для полной формы или сразу оператор, следующий после условного, для неполной формы (без Else).

Пример. Требуется составить программу вычисления площади треугольника по длинам трех сторон а, b, с. Для решения задачи используется формула Герона:

,

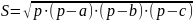где 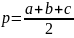— полупериметр треугольника. Исходные данные должны удовлетворять основному соотношению для сторон треугольника: длина каждой стороны должна быть меньше суммы длин двух других сторон. Имея возможность в одном условном операторе записывать достаточно сложные логические выражения, можно сразу «отфильтровать» все варианты неверных исходных данных:

Program Geron;

Var А, В, С, Р, S : Real;

Begin

WriteLn('Введите длины сторон треугольника:');

Write('а = '); ReadLn(А);

Write('b = '); ReadLn(В);

Write('с = '); ReadLn(С);

If (А > 0) And (В > 0) And (С > 0) And (А + В > С) And (В + С > A) And (А + С > В)

Then Begin

Р := (А + В + С) /2; S := sqrt(Р * (Р - А) * (Р - В) * (Р - С));

WriteLn('Площадь = ', S)

End

Else WriteLn('Неверные исходные данные')

End.

24. Программирование циклических алгоритмов

Существует три типа циклических структур: цикл с предусловием, цикл с постусловием и цикл по параметру.

Цикл с предусловием. Рассмотрим синтаксическую диаграмму оператора цикла «Пока», или цикла с предусловием. Здесь сначала вычисляется <Логическое выражение>. Пока его значение равно True, выполняется <Оператор> — тело цикла. При этом <Оператор> может быть как простым, так и составным. Для примера приведем фрагмент программы на Паскале, вычисляющий с заданной точностью е сумму гармонического ряда:

Суммирование прекращается, когда очередное слагаемое становится меньше ε или когда целая переменная I достигает значения Maxlnt:

S := 0;

I := 1;

While (1/1 >= Eps)

And (I < Maxlnt) Do

Begin

S := S + 1/1;

I := I + 1

End

Цикл с постусловием. Синтаксическая диаграмма оператора Цикла «До», или цикла с постусловием. Исполнение данного цикла повторяется до того момента, когда <Логическое выражение> станет равным True.

Предыдущая задача с использованием цикла с постусловием решается следующим образом:

S := 0;

I := 1;

Repeat S := S + 1 /1;

I := I + 1

Until (1/1 < Eps) Or (I >= Maxlnt);

Цикл по параметру. Рассмотрим задачу вычисления суммы це­ лых чисел от М до N прямым суммированием. Данную задачу можно записать в виде:

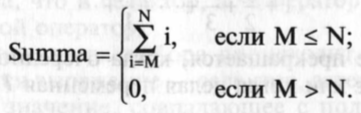
Программу с использованием структуры цикла «Пока» можно записать следующим образом:

Program Adding;

Var I, M, N, Summa : Integer;

Begin

Write('M ='); ReadLn(M);

Write('N =') ; ReadLn(N);

Summa := 0; I := M;

While I <= N Do

Begin

Summa := Summa + I;

I := Succ (I)

End;

WriteLn('Сумма равна = ', Summa)

End.

С помощью «цикл по параметру» программу на Паскале для решения данной задачи можно записать следующим образом:

Program Summering_2;

Var I, M, N, Suirana: Integer;

Begin

Write('M ='); ReadLn(M);

Write('N =') ; ReadLn(N);

Summa := 0;

For I := М То N Do

Summa := Summa + I;

WriteLn('Сумма равна = ', Summa)

End.

Переменная I принимает последовательность всех значений в диапазоне от М до N. При каждом значении I выполняется тело цикла. После последнего выполнения цикла при I = N происходит выход из цикла на продолжение алгоритма. Цикл выполнится хотя бы один раз, если М < N, и не выполнится ни разу при М > N.

25. Подпрограммы: процедуры и функции.

В языках программирования вспомогательные алгоритмы называются подпрограммами. В Паскале различают два вида подпрограмм: процедуры и функции.

Рассмотрим следующий пример: даны два натуральных числа а и Ь. Требуется определить наибольший общий делитель трех величин: а + b, |а - b|, а * b. Запишем это в виде: НОД (а + b, |а - b|, а * b). Идея решения данной задачи состоит в следующем математи­ ческом факте: если х, у, z — три натуральных числа, то НОД (х, у, z) = = НОД (НОД (х, у), z). Иначе говоря, сначала следует найти НОД двух величин, а затем НОД полученного значения и третьего числа (попробуйте это доказать). Очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения наибольшего общего делителя двух чисел. Следовательно, эта задача решается с помощью известного алгоритма Евклида

Процедуры. Программа решения исходной поставленной задачи на ТурбоПаскале будет иметь следующий вид:

Program N0D1;

Var А, В, С : Integer;

Procedure Evklid(M, N : Integer; Var К : Integer);

Begin

While M о N Do

If M > N

Then M := M – N

Else N := N - M;

К := M

End;

Begin

Write('A ='); ReadLn(A);

Write('В ='); ReadLn(B);

Evklid(A + B, Abs(A - В), C);

Evklid(C, A * В, C);

WriteLn('НОД = ' , C)

End.

В данном случае обмен аргументами и результатами между основной программой и процедурой производится через параметры (формальные и фактические).

Функции. Как и у процедуры, у функции в списке формальных параметров могут иметься параметры-переменные и параметры-значения, которые являются ее аргументами. При этом если аргументы передаются глобально, то параметры в списке могут отсутствовать. Программа решения поставленной задачи с использованием функции будет иметь вид:

Program N0D2;

Var А, В, Rez: Integer;

Function Evklid(М, N : Integer) : Integer;

Begin

While M < > N Do

If M > N

Then M := M – N

Else N := N - M;

Evklid := M

End;

Begin

Write('A = ') ; ReadLn(A);

Write('B = ') ; ReadLn(B);

Rez := Evklid(Evklid(A + B, Abs(A - B)), A * B);

WriteLn('NOD = ', Rez)

End.

Из данного примера видно, что в отличие от процедуры в теле функции результат присваивается переменной с именем функции. Обращение к функции является операндом в выражении и записывается в следующей форме:

<имя функции> (<список фактических параметров>)

Правила соответствия между формальными и фактическими параметрами у функции те же, что и у процедуры. Сравнивая рассмотренные программы, можно сделать вывод, что программа NOD2 имеет определенные преимущества перед NOD1. Функция позволяет получить результат посредством выполнения одного оператора присваивания. Здесь же показано, что фактическим аргументом при обращении к функции может быть эта же функция.