§3.6. Теорема Остроградского-Гаусса для электрического поля в диэлектриках. Вектор электрического смещения
В диэлектриках кроме свободных возникают еще и связанные заряды, т.е. те которые входят в состав молекул и возникают при поляризации. Поэтому теорема Остроградского-Гаусса приобретает вид
,
(3.25)
где
и
‑ свободные и связанные заряды,
находящиеся внутри замкнутой поверхности
.
Это уравнение неудобно для нахождения
напряженности, т.к. оно выражает
неизвестную величину
через связанные заряды
,
которые сами зависят от напряженности
поля внутри диэлектрика.
В
связи с этим величину связанных зарядов
целесообразно выразить через характеристики
самого поля. Действительно, величина
связанных зарядов находящихся на
поверхности
в пределах элементарной площадки
равна (см. §2.4)
,
(3.26)
а
заряд на всей поверхности
будет
.
(3.27)
Избыточный заряд на поверхности и заряд внутри поверхности связаны между собой соотношением
,
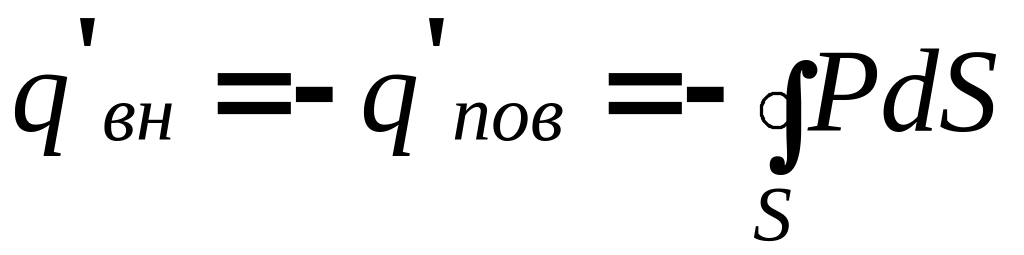(3.28)
с
мысл
которого ясен из рис.3.6.
Таким образом, связанный заряд внутри замкнутой поверхности можно выразить через вектор поляризации
.
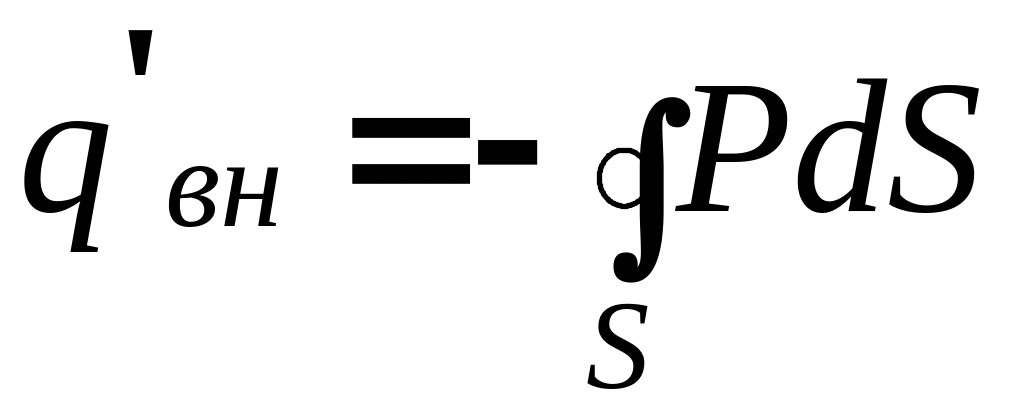(3.29)
Подставляя это выражение в уравнение, даваемое теоремой Остроградского-Гаусса, получим
,
(3.30)
или
,
(3.31)
и, наконец,
.
(3.32)
Величину
называют вектором
электрического смещения
или вектором
электрической индукции.
Поскольку вектор поляризации зависит от напряженности поля внутри диэлектрика то
,
(3.33)
где и ‑ диэлектрическая восприимчивость, и диэлектрическая проницаемость среды.
С
учетом новой характеристики поля
теорема Остроградского-Гаусса приобретает
вид:
,
(3.34)
и формулируется следующим образом: поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов находящихся внутри нее.
Отсюда становится ясным и физический смысл вектора электрического смещения – вектор электрического смещения характеризует электрическое поле только свободных зарядов. Поэтому величина вектора в вакууме и в диэлектриках одинакова. Действительно
.
(3.35)
Электрическое смещение точечного заряда и бесконечной заряженной плоскости будут
и
,
(3.36)
откуда
размерность вектора
=
.
§3.7.Условия на границе двух диэлектриков
Рассмотрим связь
между векторами
и
на
границе раздела двух однородных
изотропных диэлектриков с проницаемости
ε1
и ε2
при отсутствии на границе свободных зарядов.
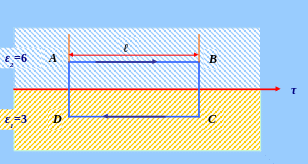
Рис.3.7.Циркуляция вектора Е на границе двух диэлектриков
Рассмотрим
циркуляцию вектора
по замкнутому контуру охватывающему
оба диэлектрика.
(3.37)
выберем АD и ВС столь малыми, что ВС · Еn + АD · Еn = 0 т.к. на участках АВ и DС направления обхода противоположны, то интегралы по этим участкам имеют разные знаки
Откуда
(3.38)
но
Е1τ
= Е2τ
(3.39)
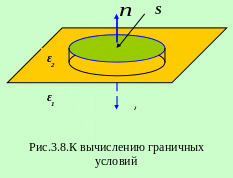
Построим прямой
цилиндр малой высоты на границе двух
диэлектриков. По теореме Гаусса
т.к. свободных зарядов нет
(3.37)
Заменив
на
получим
(3.38)
Из этих условий следует, что линии векторов и на границе диэлектриков испытывают излом
Из рисунка видно, что
(3.39)
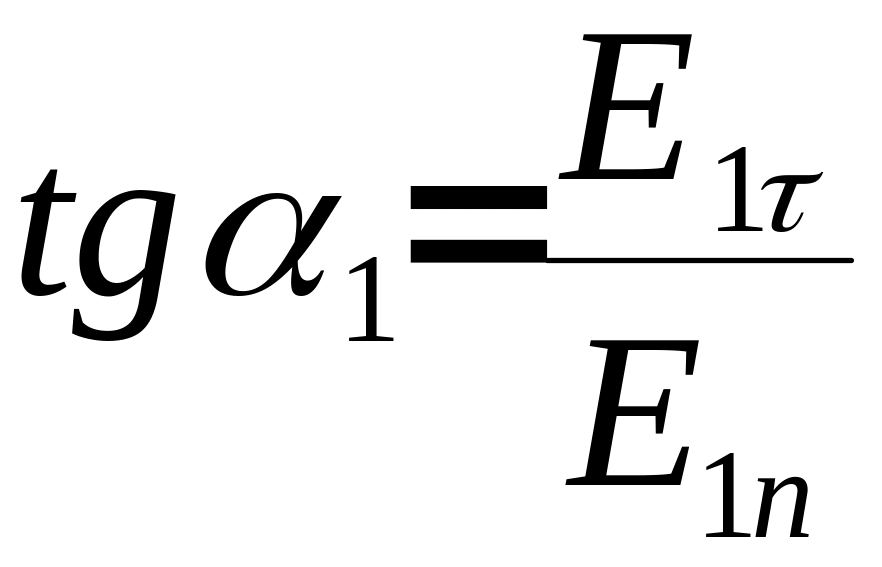(3.40)
Откуда
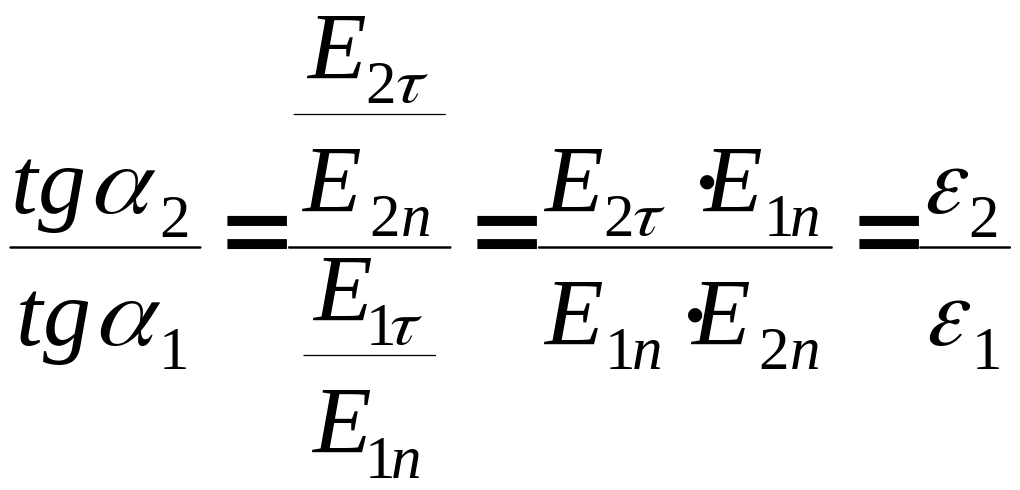(3.41)
Итак, условия на границе двух диэлектриков
E1τ
= E2τ
(3.42)
D1n
= D2n
(3.43)
(3.44)