Электромагнетизм Л-3
Глава III. Электрическое поле в диэлектриках
Диэлектриками называют вещества, в которых отсутствуют свободные носители зарядов. Диэлектрики в нормальных условиях не проводят электрический ток, т.е. являются изоляторами.
§3.1. Взаимодействие зарядов в диэлектриках.
Несмотря на отсутствие свободных зарядов, диэлектрики обладают целым рядом электрических свойств. Опыт показывает, что взаимодействие заряженных тел в диэлектриках уменьшается, по сравнению с аналогичным взаимодействием в вакууме.
Величина
,
показывающая во сколько раз сила
взаимодействия
в диэлектрике меньше чем
в вакууме, называется диэлектрической
проницаемостью.
Таким образом, в диэлектриках
.
(3.1)
Принимая
во внимание, что сила, действующая на
заряд пропорциональна напряженности
поля
,
можно заключить, что в диэлектриках
.
(3.2)
Диэлектрическая
проницаемость среды всегда больше
единицы (исключением является воздух,
для которого обычно принимается
,
хотя экспериментальное значение
).
Таким образом, законы и характеристики электрического поля, полученные для вакуума, в диэлектриках принимают вид:
закон
Кулона 
;
(3.3)
напряженность
точечного заряда 
;
(3.4)
потенциал
точечного заряда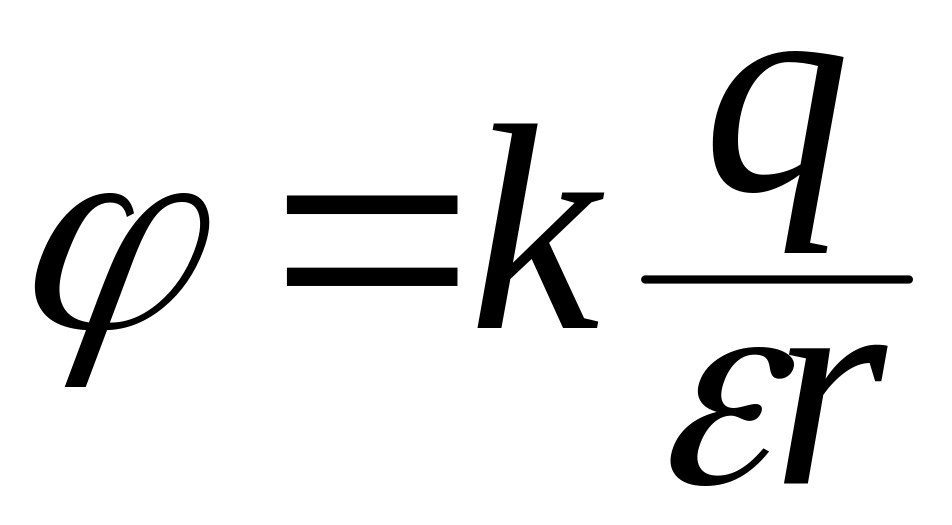 
;
(3.5)
напряженность
заряженной нити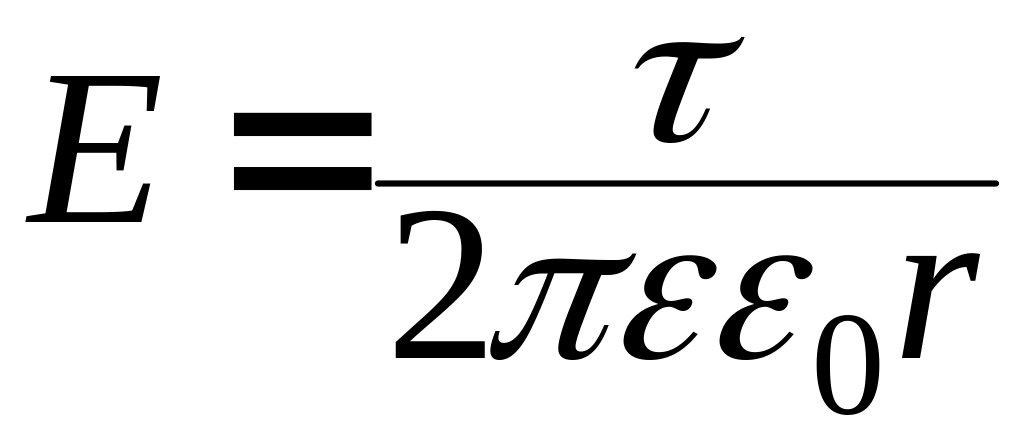 
;
(3.6)
напряженность
поля заряженной плоскости 
.
(3.7)
§3.2. Полярные и неполярные молекулы
Электрические свойства диэлектриков можно понять, рассматривая их строения на молекулярном уровне. Каждая молекула или атом вещества состоит из положительных ядер и отрицательных электронов. Причем количество положительных равно числу отрицательных зарядов, так что в целом молекула электрически нейтральна.
В первом приближении суммарное действие положительных зарядов может быть заменено действием одного положительного заряда, а суммарное действие отрицательных зарядов – одним точечным отрицательным зарядом. Усредненное положение положительных и отрицательных зарядов определятся точно так же как и центр масс системы материальных точек, а именно:
,
(3.8)
здесь
суммирование ведется по всем зарядам
молекулы, положение которых определяются
радиус-векторами
.
Если
молекула несимметрична, то положительные
и отрицательные заряды пространственно
разделены, т.е.
.
Такие молекулы называются полярными
и могут рассматриваться как электрический
диполь, т.е. систему двух связанных
одинаковых по величине точечных зарядов
и
.
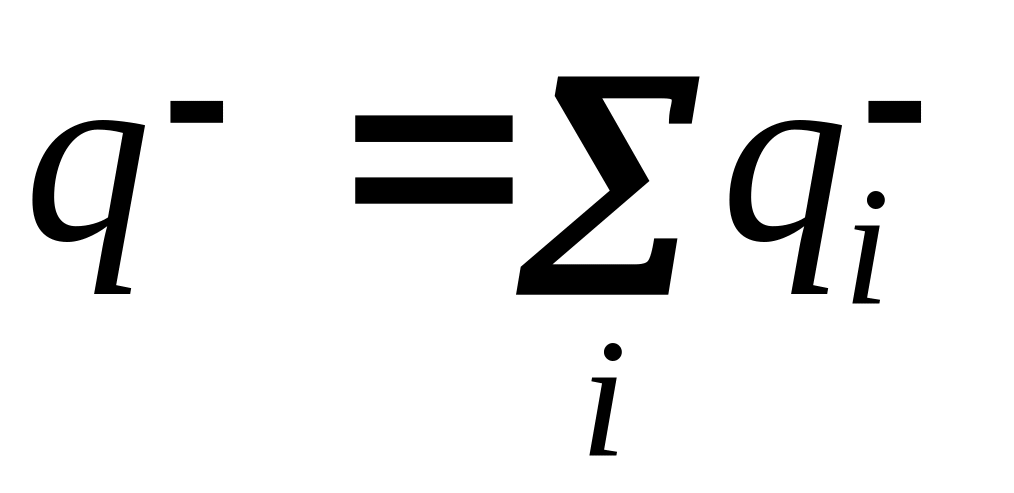Молекулы
полярных диэлектриков характеризуются
дипольным моментом
,
напряженность поля которого
(см. §1.4). К полярным молекулам относятся,
например,
и др.
В
атомах и симметричных молекулах таких
как,
и т.п., центры положительных и отрицательных
зарядов совпадают. Поэтому
и
,
т.к.
.
Эти вещества относятся к неполярным
диэлектрикам.
§3.3. Молекулы в электрическом поле
Действие электрического поля на молекулы полярного диэлектрика приводит к появлению у каждой из них вращательного момента, который стремится повернуть диполь вдоль силовых линий поля (рис.3.1).
Величина
вращательного момента пары сил, как
видно из рисунка, определяется следующим
образом (в однородном поле
):
,
(3.9)
т.е.
или
.
(3.10)
Таким
образом, молекулы с постоянным дипольным
моментом стремятся ориентироваться
так, чтобы направления диполей совпадали
с направлением внешнего поля
.
Е
сли
в электрическое поле помещен неполярный
диэлектрик,
то положительные и отрицательные заряды
смещаются
друг относительно друга. Положительные
вдоль поля, а отрицательные в противоположную
сторону. В результате молекула приобретает
наведенный
(индуцированный)
дипольный момент, который называют
упругим
дипольным моментом.
Индуцированный
дипольный момент пропорционален
:
,
(3.11)
здесь
коэффициент
‑ называется поляризуемостью
молекулы.