§1.6. Теорема Остроградского-Гаусса.

Теорема Остроградского-Гаусса связывает величину потока через замкнутую поверхность с зарядом, который находится внутри нее. Качественно, наличие этой связи видно из рисунка 1.6. Чем больше заряд, тем больше напряженность, следовательно, гуще силовые линии и больше их количество, т.е. поток.

Рассмотрим поле одного точечного заряда . Проведем вокруг него сферу радиуса r (рис.1.6.2). Вектор напряженности в каждой точке сферы имеет одинаковое значение и перпендикулярен ее поверхности ( ). Таким образом поток через сферу будет равен

. (1.29)

Используя выражение для напряженности точечного заряда, получим:

. (1.30)

Видно, что поток через сферу не зависит от ее радиуса. Из рисунка 1.6.2 следует также, что тот же поток (число силовых линий) будет пронизывать и произвольную поверхность (такая поверхность называется гауссовой).

Таким образом

. (1.31)

Рис.1.7.Поток вектора Е через сложную поверхность

Полученный результат несложно обобщить на случай нескольких зарядов внутри сферы. Для этого нужно воспользоваться принципом суперпозиции полей:

. (1.32)

Ясно, что для произвольного числа зарядов справедливо соотношение:

. (1.33)

Последнее выражение представляет собой математическую форму теоремы Остроградского-Гаусса: поток вектора напряженности через произвольную замкнутую поверхность, пропорционален алгебраической сумме зарядов, заключенных внутри нее.

Если заряд распределен в пространстве с объемной плотностью , то теорема Остроградского-Гаусса записывается в виде:

, (1.34)

здесь интегрирование ведется по всему объему V ограниченному поверхностью S.

Главным при доказательстве теоремы Остроградского-Гаусса является непрерывность силовых линий, а также то, что они всегда начинаются на положительных и заканчиваются на отрицательных зарядах. Поэтому, если из объема выходит больше линий, чем входит в него, то внутри объема должен находиться положительный заряд; если входит линий больше, чем выходит, то внутри должен быть отрицательный заряд. Конечно, линии поля могут входить в объем, внутри которого суммарный заряд равен нулю, но тогда число входящих равно числу выходящих линий. Поэтому суммарный поток равен нулю (рис.1.8).

Эти простые соображения не зависят от того, как распределен электрический заряд внутри поверхности. Заряд может находиться в центре или вблизи поверхности. Более того, внутри может находиться множество зарядов, как положительных, так и отрицательных, расположенных в любой точке.

§1.7. Расчет напряженности электрического поля на основе теоремы Остроградского-Гаусса

Поле объемно-заряженного шара.

Если шар радиуса R равномерно заряжен с объемной плотностью , то его заряд равен . Электрическое поле такого заряженного тела будет сферически симметричным (рис.1.7.1).

1. Для расчета поля внутри шара построим гауссову поверхность в виде сферы радиуса . Т.к. поле радиально и заряд внутри распределен равномерно, значения во всех точках поверхности будут одинаковы. Силовые линии перпендикулярны поверхности сферы, поэтому:

. (1.35)

Согласно теореме Остроградского-Гаусса этот поток пропорционален заряду внутри поверхности , который равен

. (1.36)

Таким образом,

,

откуда

. (1.37)

Напряженность поля внутри шара линейно возрастает (с увеличением поверхность охватывает все больший заряд).

2. Поток вектора через поверхность радиуса вычисляется аналогично, т.е.

. (1.38)

Заряд находящийся внутри равен заряду шара Q. Поэтому на основании теоремы Остроградского-Гаусса

и , (1.39)

т.е. поле вне заряженного шара такое же, как у точечного заряда, помещенного в центр шара.

Зависимость напряженности электростатического поля как функция расстояния от центра шара показана на рис.1.7, где напряженность на поверхности определяется выражением

. (1.40)

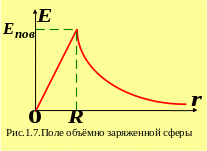
Поле заряженной сферы.

Поскольку заряд распределен только на поверхности сферы, то внутри он отсутствует. Значит поток через любую поверхность с радиусом , по теореме Остроградского-Гаусса, равен нулю, а значит и напряженность внутри сферы .

Поток через гауссову поверхность при вычисляется точно также, как и для шара. Следовательно,

, (1.41)

где ‑ расстояние от центра сферы.

Зависимость напряженности от расстояния до центра сферы показана на рис.1.7.

Поле равномерно заряженной бесконечной нити (цилиндра).

Из соображений симметрии следует, что линии напряженности будут направлены радиально, с одинаковой густотой во все стороны относительно нити.

Для применения теоремы Остроградского-Гаусса замкнутую поверхность целесообразно выбрать в виде цилиндра радиуса с осью, совпадающей с нитью (рис.1.7.4). Поток вектора через верхнюю и нижнюю грань цилиндра равен нулю, а через боковую поверхность площадью , равен

.(через торцы цилиндра Ф = 0, т.к. Е_n = 0)

Заряд внутри цилиндра равен , где ‑ линейная плотность заряда. Тогда на основании теоремы Остроградского–Гаусса получим

,

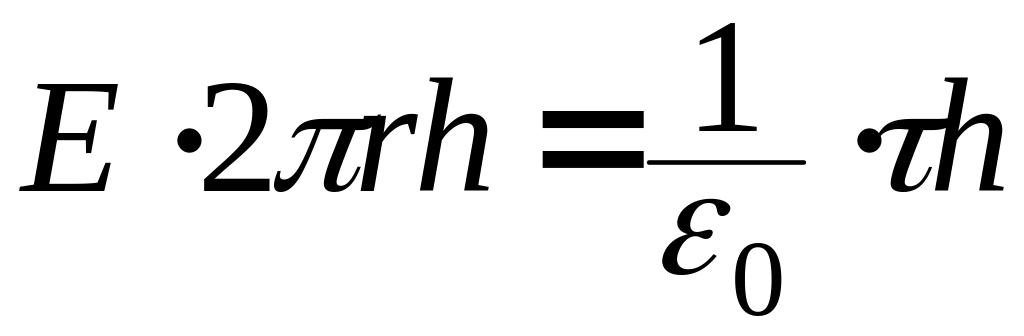и окончательно

. (1.41)

Поле бесконечной равномерно заряженной плоскости.

Заряженная плоскость с поверхностной плотностью заряда создает однородное (напряженность во всех точках одинакова) электрическое поле, силовые линии которого перпендикулярны ее поверхности. В качестве замкнутой поверхности удобно взять цилиндр, основания которого параллельны плоскости (рис.1.7). Суммарный поток через такую поверхность равен

. (1.42)

Через боковую поверхность поток равен нулю, т.к. вектора и нормаль в любой точке взаимно перпендикулярны. Таким образом

.

Заряд, находящийся внутри цилиндра , поэтому

,

откуда

. (1.43)