Бернулли заңы

Уикипедия — ашық энциклопедиясынан алынған мәлімет

Бернулли теңдеуі^[1] — гидромеханиканың негізгі теңдеулерінің бірі. Бұл теңдеуді швейцариялық ғалым Д. Бернулли (1700 —1782) өзінің 1738 жылы Страсбургте жарық көрген “Гидродинамика” деген еңбегінде тұжырымдаған.

1. Бернулли теңдеуі біртекті ауырлық күші өрісіндегі сығылмайтын сұйықтықтың бірқалыпты қозғалысы үшін төмендегіше өрнектеледі:

 — сұйықтық тығыздығы,

 — сұйықтық жылдамдығы,

 — белгілі бір горизонталь жазықтықтан бастап есептелетін сұйықтық бөлшектерінің биіктігі,

 — сұйықтық қысымы,

 — еркін түсу үдеуі.

(1) теңдеудің сол жағындағы алғашқы екі мүшесінің қосындысы сұйықтықтың (бірлік массаға қатысты) толық потенциалдық энергиясына, ал үшінші мүшесі сұйықтықтың кинетикалық энергиясына тең. Демек, тұтас алғанда теңдеу қозғалыстағы сұйық ағыны үшін механикалық энергияның сақталу заңын өрнектейді әрі  , р және һ арасындағы негізгі тәуелділікті белгілейді. Бернулли теңдеуін төмендегіше түрде де өрнектеуге болады:

 немесе

, (2),

мұндағы m =   — сұйықтықтың меншікті салмағы. (1) теңдіктегі барлық қосылғыштың ұзындық өлшемдері бар және олар сәйкес түрде геометриялық (нивелирлік), пьезометрлік және жылдамдық биіктігі деп, ал (2) теңдіктегі барлық қосылғыштың қысымдық өлшемдері бар және олар сәйкес түрде салмақтық, статикалық және динамикалық қысым деп аталады.

Идеал газ үшін[өңдеу]

^[2] (ток сызықтары бойында тұрақты)

мұндағы

 — газдың адиабаттық тұрақтысы

 — газдың нүктедегі қысымы

 — газдың нүктегі тығыздығы

 — газдың ағу жылдамдығы

 — еркін құлау үдеуі

 — салыстырмалы координаттар басынан биіктігі

Біртекті емес өрісте қозғалса   гравитациялық өріс потенциалымен алмастырылуы керек.

Бернулли заңының термодинамикасы[өңдеу]

Статистикалық физикадан адиабаттық ағыста ток сызықтарында келесі шамалар тұрақты болады:

мұндағы   — масса бірлігініңэнтальпиясы,   — күш потенциалы.

Жалпыланған Бернулли теңдеуінде (1) және (3) түріндегі теңдеулер сақтала отырып, олардың сол жағына үйкеліс күшініңжұмысы мен гидравликалық кедергіге жұмсалатын жұмыс, сондай-ақ, сұйықтықтың не газдың механикалық жұмысы (компрессордың не турбинаның жұмысы) өз таңбасымен қосылады. Жалпыланған Бернулли теңдеуі гидравликада, машина жасауда, т.б. кеңінен қолданылады. ^[3]

Пайдаланылған әдебиет[өңдеу]

1. Жоғарыға көтеріліңіз↑ Орысша-қазақша түсіндірме сөздік: Механика / Жалпы редакциясын баскарған э.ғ.д., профессор Е. Арын - Павлодар : «ЭКО»ҒӨФ. 2007.-29 1 б. ISBN 9965-08-234-0

2. Жоғарыға көтеріліңіз↑ Clancy, L.J., Aerodynamics, Section 3.11

3. Жоғарыға көтеріліңіз↑ “Қазақ Энциклопедиясы”, II-том

Bernoulli's principle

From Wikipedia, the free encyclopedia

This article is about Bernoulli's principle and Bernoulli's equation in fluid dynamics. For Bernoulli's theorem in probability, see law of large numbers. For an unrelated topic in ordinary differential equations, see Bernoulli differential equation.

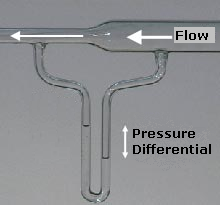
A flow of air into a venturi meter. The kinetic energy increases at the expense of the fluid pressure, as shown by the difference in height of the two columns of water.

‹ The template Continuum mechanics is being considered for merging. ›

Continuum mechanics

Laws[show]

Solid mechanics[show]

Fluid mechanics[show]

Rheology[show]

Scientists[show]

v t e

In fluid dynamics, Bernoulli's principlestates that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy.^[1][2] The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738.^[3]

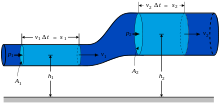
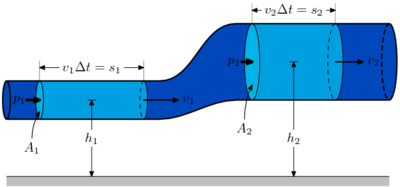
Bernoulli's principle can be applied to various types of fluid flow, resulting in what is loosely denoted as Bernoulli's equation. In fact, there are different forms of the Bernoulli equation for different types of flow. The simple form of Bernoulli's principle is valid for incompressible flows (e.g. most liquid flows) and also for compressible flows (e.g. gases) moving at low Mach numbers (usually less than 0.3). More advanced forms may in some cases be applied to compressible flows at higher Mach numbers (see the derivations of the Bernoulli equation).

Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of mechanical energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy and potential energy remain constant. Thus an increase in the speed of the fluid occurs proportionately with an increase in both its dynamic pressure and kinetic energy, and a decrease in its static pressure and potential energy. If the fluid is flowing out of a reservoir, the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit volume (the sum of pressure and gravitational potential ρ g h) is the same everywhere.^[4]

Bernoulli's principle can also be derived directly from Newton's 2nd law. If a small volume of fluid is flowing horizontally from a region of high pressure to a region of low pressure, then there is more pressure behind than in front. This gives a net force on the volume, accelerating it along the streamline.^[5][6][7]

Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.