- •14) Запас прочности.
- •15) Опускаемые напряжения
- •Условие жесткости
- •Недостатки клеевых соединений
- •Балки постоянного поперечного сечения из пластичных материалов
- •37) Понятие о линейных и угловых перемещениях при изгибе
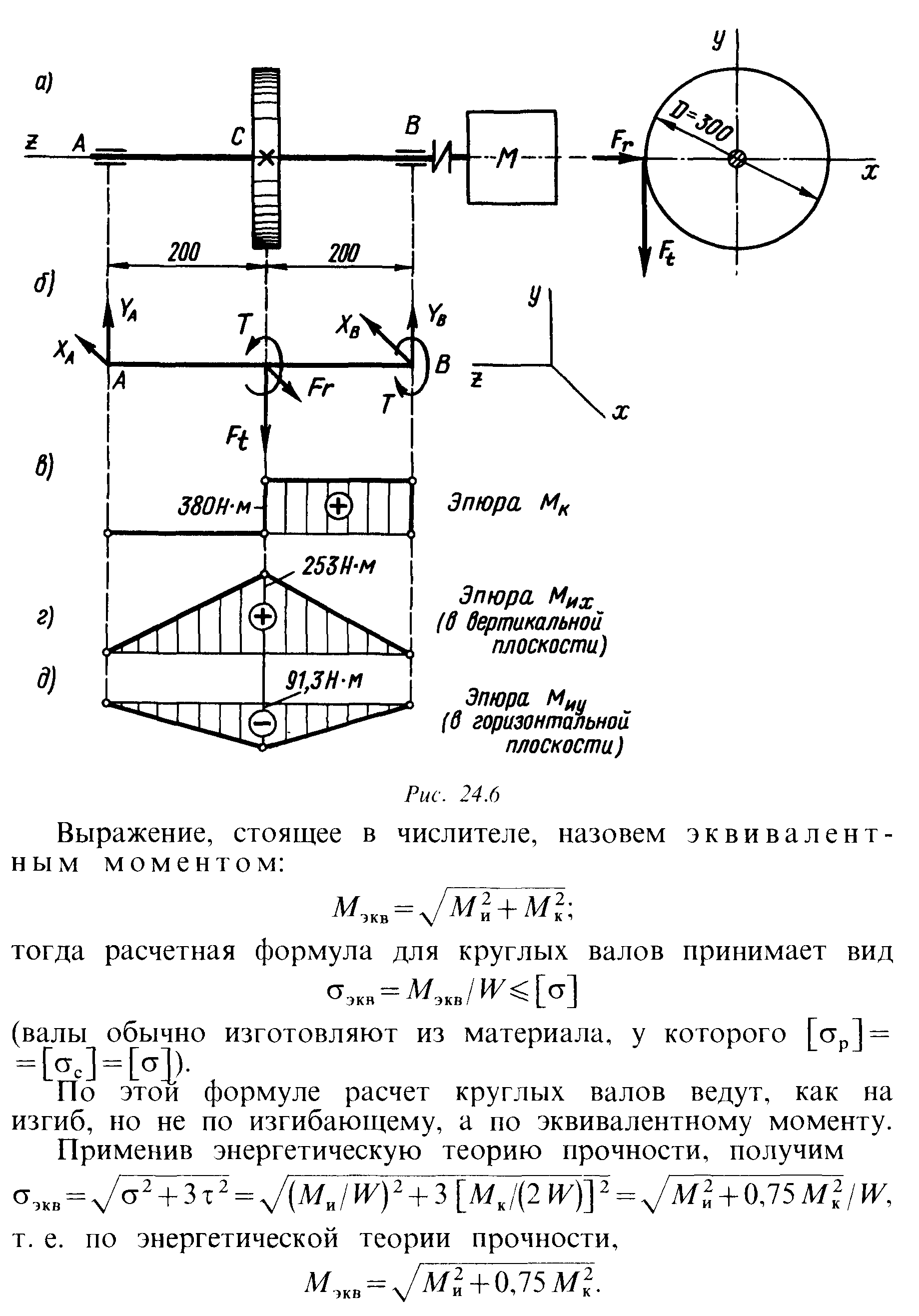
- •43) Расчет валов на изгиб с кручением
- •46) Критическое напряжение. Пределы применимости формулы эйлера
- •50) Детали машин
- •Требования, предъявляемые к деталям машин
- •Классификация валов и осей
- •Критерии работоспособности валов и осей
- •Расчёты валов и осей
- •Система классификации муфт По видам управления
- •По группам муфт (механические)
37) Понятие о линейных и угловых перемещениях при изгибе
При изгибе, как установлено в предыдущих параграфах, под действием поперечных нагрузок продольная ось бруса (балки) искривляется. Если изгиб протекает в пределах упругих свойств материала, т. е, в пределах действия закона Гука, то после снятия нагрузок ось бруса снова выпрямляется. Поэтому изогнутую ось бруса называют упругой линией. По форме, которую при нагружении бруса принимает его упругая линия, можно судить об угловых и линейных перемещениях при изгибе. Изобразим продольную ось защемленной одним концом балки (рис. 1). Под действием нагрузки F, перпендикулярной оси балки и расположенной в главной плоскости, ось, оставаясь в этой плоскости, изгибается и принимает вид отрезка кривой. Рассматривая изогнутую ось балки (рис. 1), исходя из принятого допущения о незначительности перемещения точек тела при упругих деформациях, видим следующее.
Центры
тяжести произвольных сечений 1 и 2 при
изгибе балки переместились соответственно
на расстояния
 и
и
 ,
а сами сечения, оставаясь плоскими (по
гипотезе плоских сечений), повернулись
на углы
,
а сами сечения, оставаясь плоскими (по
гипотезе плоских сечений), повернулись
на углы
 и
.
и
.
Так
как при повороте сечения остаются
перпендикулярными к изогнутой оси
бруса, то угол поворота
![]() произвольного
поперечного сечения бруса равен углу
между касательной к изогнутой оси в
данной точке и направлением оси
недеформированного бруса.
Линейные
перемещения центров тяжести произвольных
поперечных сечений при изгибе называются
прогибами бруса в соответствующих
точках, а наибольший прогиб обозначается
произвольного
поперечного сечения бруса равен углу
между касательной к изогнутой оси в
данной точке и направлением оси
недеформированного бруса.
Линейные
перемещения центров тяжести произвольных
поперечных сечений при изгибе называются
прогибами бруса в соответствующих
точках, а наибольший прогиб обозначается
![]() и
называется стрелой прогиба. На рис. 1
стрела прогиба образовалась в точке
В.
Существует несколько способов
определения перемещений сечений при
изгибе. Один из них основан на
дифференцировании уравнения упругой
линии. Для вывода этого уравнения
используется формула,
выражающая зависимость между кривизной
и
называется стрелой прогиба. На рис. 1
стрела прогиба образовалась в точке
В.
Существует несколько способов
определения перемещений сечений при
изгибе. Один из них основан на
дифференцировании уравнения упругой
линии. Для вывода этого уравнения
используется формула,
выражающая зависимость между кривизной
![]() и
изгибающим моментом
и
изгибающим моментом
![]() .
При этом следует иметь в виду, что правило
знаков для кривизны изогнутой оси
связано с выбранными направлениями
осей координат. Если принять, что ось х
направлена вправо, а ось у - вниз, как
показано на рис. 1, то кривизна оси
балки положительна в том случае, когда
при изгибе балка обращена вогнутостью
вниз, и отрицательна, когда балка обращена
вогнутостью вверх, т. е. положительному
изгибающему моменту соответствует
отрицательная кривизна, а отрицательному
- положительная кривизна. В соответствии
с этим перепишем формулу
в следующем виде:
.
При этом следует иметь в виду, что правило
знаков для кривизны изогнутой оси
связано с выбранными направлениями
осей координат. Если принять, что ось х
направлена вправо, а ось у - вниз, как
показано на рис. 1, то кривизна оси
балки положительна в том случае, когда
при изгибе балка обращена вогнутостью
вниз, и отрицательна, когда балка обращена
вогнутостью вверх, т. е. положительному
изгибающему моменту соответствует
отрицательная кривизна, а отрицательному
- положительная кривизна. В соответствии
с этим перепишем формулу
в следующем виде:
![]() .
С другой стороны, из курса математики
известно, что в системе координат (х, у)
кривизна упругой линии при малых
перемещениях
сечений может быть
выражена равенством
.
С другой стороны, из курса математики
известно, что в системе координат (х, у)
кривизна упругой линии при малых
перемещениях
сечений может быть
выражена равенством
![]() .
Сопоставив
друг с другом два последних равенства,
получаем дифференциальное уравнение
упругой линии балки
.
Сопоставив
друг с другом два последних равенства,
получаем дифференциальное уравнение
упругой линии балки
![]() .
Интегрируя
это уравнение для каждого конкретного
случая нагружения балки, можно определить
сначала угол поворота заданного
сечения:
.
Интегрируя
это уравнение для каждого конкретного
случая нагружения балки, можно определить
сначала угол поворота заданного
сечения:
![]() ,
а
затем его прогиб:
,
а
затем его прогиб:
![]() .
Если
балка имеет несколько участков нагружения,
то уравнение
составляют для каждого участка в
отдельности. После двойного интегрирования
каждого из этих уравнений образуется
по две произвольных постоянных, которые
необходимо определить. Решение получается
очень громоздким. Поэтому чаще всего
для определения перемещений сечений
балок используют более рациональный
способ с помощью интеграла Мора.
.
Если
балка имеет несколько участков нагружения,
то уравнение
составляют для каждого участка в
отдельности. После двойного интегрирования
каждого из этих уравнений образуется
по две произвольных постоянных, которые
необходимо определить. Решение получается
очень громоздким. Поэтому чаще всего
для определения перемещений сечений
балок используют более рациональный
способ с помощью интеграла Мора.
Расчет на жесткость при изгибе
В
практических расчетах нередки случаи,
когда в балке, сечение которой выбрано
из условия прочности, перемещения
оказываются большими - превышающими
установленные для них нормы. Поэтому,
кроме расчета на прочность, балки должны
проверяться также и на жесткость.
Обозначив допускаемую стрелу прогиба
через [(],
получим
условие жесткости балки
![]()
Допускаемые значения стрелы прогиба зависят от назначения конструкции и колеблются в достаточно широких пределах. Так, например, в строительных конструкциях допускаемые значения относительных прогибов колеблются от 1/150 до 1/400. При расчете валов допускаемый относительный прогиб обычно ограничивается 1/1000.
38)
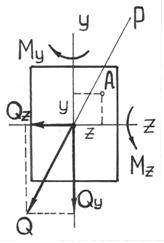
Косой изгиб – изгиб, при котором
плоскость P действия изгибающих
момент ов
и поперечных сил не совпадает ни с одной
из главных плоскостей инерции бруса.
ов
и поперечных сил не совпадает ни с одной
из главных плоскостей инерции бруса.
|
Определение внутренних усилий при косом изгибе. При косом изгибе в поперечных сечениях бруса действуют следующие внутренние усилия: Mz, My – изгибающие моменты и Qy, Qz –поперечные (перерезывающие) силы. Это легко показать мысленно рассекая стержень и определяя внутренние усилия при косом изгибе консольной балки под действием сосредоточенной силы F на свободном конце (см. рис.47):
39) при
косом изгибе условие прочности принимает
вид:
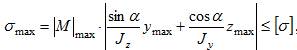 (
5 )
Если моменты сопротивления
сечения относительно главных осей
инерции могут быть выражены через
размеры сечения , условие прочности
удобно использовать в таком виде:
(
5 )
Если моменты сопротивления
сечения относительно главных осей
инерции могут быть выражены через
размеры сечения , условие прочности
удобно использовать в таком виде:
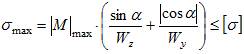 (
6 )
При подборе сечений один из
осевых моментов сопротивления выносят
за скобки и задаются соотношением . Зная
, и угол , путем последовательных попыток
определяют значение и , которые
удовлетворят условию прочности :
(
6 )
При подборе сечений один из
осевых моментов сопротивления выносят
за скобки и задаются соотношением . Зная
, и угол , путем последовательных попыток
определяют значение и , которые
удовлетворят условию прочности :
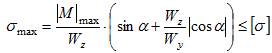 (
7 )
Для несимметричных сечений ,
не имеют выступающих углов , используется
условие прочности в виде (5). В этом случае
при каждой новой попытке расчета размеров
сечения необходимо заранее вновь обрести
положение нулевой линии и координаты
самой удаленной от нулевой линии точки
( ) . Для прямоугольного сечения . Задаваясь
соотношением , из условия прочности ( 7
) легко найти величину и размеры
поперечного сечения .
(
7 )
Для несимметричных сечений ,
не имеют выступающих углов , используется
условие прочности в виде (5). В этом случае
при каждой новой попытке расчета размеров
сечения необходимо заранее вновь обрести
положение нулевой линии и координаты
самой удаленной от нулевой линии точки
( ) . Для прямоугольного сечения . Задаваясь
соотношением , из условия прочности ( 7
) легко найти величину и размеры
поперечного сечения .
40)



41)
Изгиб с растяжением (сжатием)
Расчеты на совместное действие изгиба и растяжения можно свести к следующим двум основным видам:
а) расчеты на действие продольно поперечных нагрузок;
б) расчеты на внецентренное растяжение – сжатие
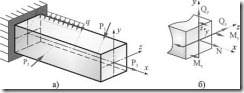
Если
на балку действуют и продольные и
поперечные нагрузки, пересекающие ось
бруса (рис. 2.6.4, а), то в общем случае в
поперечных сечениях возникают изгибающие
моменты
![]() и
и
![]() ,
поперечные силы
,
поперечные силы
![]() и
и
![]() ,
а так же продольная сила
,
а так же продольная сила
![]() (рис.2.6.4,
б). Таким образцом, в этом случае будет
сложный изгиб с растяжением (сжатием).
Нормальные напряжения в произвольной
точке сечения
(рис.2.6.4,
б). Таким образцом, в этом случае будет
сложный изгиб с растяжением (сжатием).
Нормальные напряжения в произвольной
точке сечения
![]() (2.6.6)
(2.6.6)
А условие прочности имеет простейший вид:
 (2.6.7)
(2.6.7)
Внецентренное растяжение-сжатие
стержня (в сопротивлении материалов), деформация, возникающая при действии на стержень двух равных и противоположно направленных продольных сил, параллельных оси стержня; один из видов сложного сопротивления (См. Сложное сопротивление). В. р.-с. характеризуется сложением деформаций от изгиба и от продольных сил. При В. р.-с. в точках поперечного сечения с текущими координатами у и z, взятыми относительно главных центральных осей (рис.), нормальные напряжения определяются по формуле:
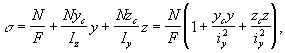
в которой F — площадь поперечного сечения, Iy и Iz — моменты инерции сечения, iy и iz — радиусы инерции сечения, ус и zc — координаты точки приложения продольной силы N. Нормальные напряжения линейно зависят от координат и достигают максимальных значений в точках поперечного сечения, наиболее удалённых от нейтральной линии, положение которой определяется отрезками ау и az, отсекаемыми на координатных осях:
![]()
Если продольная сила приложена в границах ядра сечения (См. Ядро сечения), то нейтральная линия либо лежит за пределами сечения, либо касается контура сечения, при этом эпюра нормальных напряжений становится однозначной. Случаи В. р.-с. часто встречаются при расчётах фундаментов, арок, рам и других конструкций.
42)