Балки постоянного поперечного сечения из пластичных материалов

Пластичные материалы одинаково сопротивляются как растяжению, так и сжатию: в связи с этим для них Поэтому балки из пластичных материалов обычно имеют поперечные сечения, симметричные относительно своих нейтральных осей, при которых в балках возникают одинаковые наибольшие растягивающие и сжимающие напряжения.

В рассматриваемом случае опасным является то поперечное сечение балки, в котором возникает наибольший по абсолютной величине изгибающий момент Мтах. Для этого сечения и составляется условие прочности. Опасными являются точки опасного поперечного сечения, наиболее удаленные от нейтральной оси.

Нормальные напряжения в этих точках определяются [в соответствии с выражением (21.7)] по формуле

Здесь для упрощения индекс при М и W не указан.

Заметим, что в крайних точках поперечного сечения касательные напряжения равны нулю и, следовательно, напряжения <тшах, определяемые по формуле (42.7), являются главными.

Подставив значение атзх из выражения (42.7) в условие прочности (41.7), получим формулу для проверки напряжений (формулу проверочного расчета):

34)

Расчеты на прочность при поперечном изгибе

При поперечном изгибе наибольшие нормальные напряжения возникают в наиболее удаленных от нейтральной оси точках сечения, а на самой этой оси нормальные напряжения равны нулю, тогда как зона действия наибольших касательных напряжений расположена, наоборот, вблизи нейтральной оси. Кроме того, величина т_тах мала по сравнению с о_таХ1 если длина балки существенно больше высоты сечения. Все это позволяет не принимать во внимание касательные напряжения и проводить расчет на прочность только по нормальным напряжениям (для тонкостенных балок это не всегда справедливо).

Услоеие прочности балки требует, чтобы максимальные нормальные напряжения не превышали допускаемых напряжений для материала балки:

Если материал одинаково работает на растяжение и сжатие, то опасной будет та точка сечения, где действует наибольшее по абсолютной величине напряжение независимо от его знака. Для хрупких материалов, имеющих существенно различные пределы прочности при растяжении и сжатии требуется проверка прочности по наибольшим растягивающим и сжимающим напряжениям: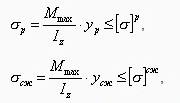

Для балок из пластичных материалов, одинаково работающих на растяжение и сжатие, целесообразно выбирать сечения, симметричные относительно их нейтральных осей; при этом условии обеспечивается одинаковый запас прочности сечения по растянутым и сжатым волокнам.

Если кроме условия прочности исходить еще и из требования минимальной массы балки, то наиболее рациональным будет сечение, которое при заданном моменте сопротивления имеет наименьшую площадь сечения, а при заданной площади - наибольший момент сопротивления. Поэтому двутавровое сечение имеет существенное преимущество перед прямоугольным сечением.

Для материалов хрупких, обладающих различной прочностью при растяжении и сжатии, рациональным будет сечение, несимметричное относительно нейтральной оси, например тавровое, несимметричное двутавровое и т.п.

35)

Э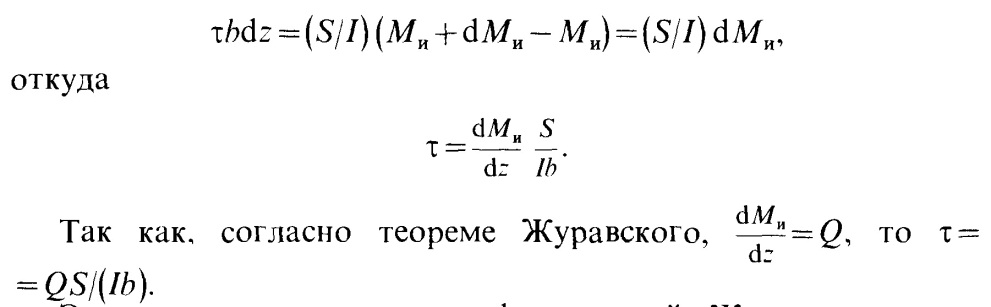 то равенство называется формулой Журавского.

Выведенная формула дает значение касательных напряжений в продольных сечениях, но по закону парности в точках поперечного сечения, лежащих на линии пересечения продоль­ной и поперечной плоскостей, будут действовать одинаковые по модулю касательные напряжения.

Формула Журавского читается так: касательные напряжения в поперечном сечении балки равны произведению поперечной силы (2 на статический момент 8 относительно нейтральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину Ь рассматриваемого слоя волокон.

36) Условие прочности по касательным напряжениям

 

,

 

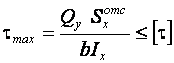
где  – наибольшее по модулю напряжение в поперечном сечении;  – допускаемые касательные напряжения.

Если для материала балки заданы различные допускаемые нормальные напряжения при растяжении и сжатии, то условия прочности применяют отдельно к наиболее растянутым и к наиболее сжатым волокнам балки.