Недостатки клеевых соединений

1) сравнительно невысокая прочность, в особенности при неравномерном отрыве; 2) относительно невысокая долговечность некоторых клеев («старение»); 3) низкая теплостойкость; 4) необходимость соблюдения мер по технике безопасности (установка приточно-вытяжной вентиляции); 5) для большинства соединений требуется нагрев, сжатие и длительная выдержка соединяемых деталей.

22) Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы.

При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения

Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4, а).

23) Напряжения и деформации при кручении бруса круглого поперечного сечения

Под действием внешнего скручивающего момента, приложенного на правом конце вала (рис. 7.2), левый конец которого жестко закреплен, стержень будет закручиваться. При этом любое сечение стержня, оставаясь плоским, будет поворачиваться на некоторый угол <р_к, называемый углом закручивания. Этот угол изменяется по длине вала от нуля в заделке до максимального на правом конце вала. При этом образующая внешней цилиндрической поверхности вала повернется на угол у, называемый углом сдвига. Этот угол изменяется вдоль радиуса сечения от нуля на оси вала до - у_тах на внешней поверхности. Опыт показывает, что после закручивания бруса круглого сечения поперечные линии, нанесенные на его поверхности, остаются плоскими, а диаметры сечений и расстояния между ними не изменяются. При этом прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных сечениях бруса, а по закону парности касательных напряжений - и в продольных его сечениях, то есть напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг На основании опыта вводятся следующие гипотезы

1. Нормальные напряжения в поперечных сечениях отсутствуют (иначе изменялись бы расстояния между сечениями).

2. Поперечные сечения при кручении остаются плоскими.

3. Радиусы в поперечных сечениях остаются прямолинейными (не искривляются).

24) Деформации при кручении и условие жесткости вала

Из выражения (5.5) следует, что

,

интегрируя которое по длине вала, получим:

.

Если М_к = const и = const по всей длине вала, то

,

где - жесткость вала при кручении.

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания

.

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:

.

Эта формула выражает условие жесткости вала при кручении. Обычно принимается на 1 м длины вала.

25) Полярный момент инерции круглого сечения - Взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадраты их расстояний до начала координат (центра тяжести сечения).

Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м⁴, см⁴) и может быть лишь положительной.

26) При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его проч­ности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

2) выбирают материал для рассчитываемого вала и определяют для этого ма­териала допускаемое напряжение, например по формуле (5.9), ;

3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

Для сплошного круглого сечения , отсюда можем записать вы­ражение для определения диаметра вала из условия его прочности:

Для кольцевого сечения

27) Определив размеры вала из условия прочности, проверяют вал на жесткость.

Условие жесткости требует, чтобы максимальный относительный угол закручивания , был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

. (5.11)

Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:

но W_ρ = 0,2d³, поэтому

(5.12)

Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала

В этой формуле допускаемый относительный угол закручивания должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения I_p будет выглядеть следующим образом:

но I_p = 0,1d ⁴ , поэтому

(5.13)

Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.

В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего d_вн и наружного диаметров d, т.е. при заданном параметре k = d_вн /d, формулы (5.12) и (5.13) принимают вид:

(5.14)

(5.15)

28) - простой (плоский, прямой) изгиб - вид нагружения, при котором плоскость

действия изгибающего момента (силовая плоскость) проходит через одну из главных

центральных осей поперечного сечения стержня. Примером таких осей являются оси

симметрии сечения.

Балки воспринимают нагрузку от внешних сил и передают их другим частям конструкции,

которые поддерживают балку. По отношению к балке эти части выступают как опоры.

Если брус находится под действием двух пар сил (см. рис. 228,д), расположенных в плоскости его продольной оси, то возникает деформация изгиба. При деформации изгиба часть волокон удлиняется, а часть становится короче. Между зонами растяжения и сжатия располагается нейтральный слой.

В нейтральном слое волокна не подвергаются деформации и сохраняют свою длину неизменной. Чем дальше волокна расположены от нейтрального слоя, тем большую деформацию они испытывают.

Таким образом, при изгибе в поперечных сечениях бруса под действием внутренних сил возникают нормальные напряжения растяжения и сжатия, и их величина зависит от положения точки в сечении. Наибольшие напряжения возникают в наиболее удаленных точках от нейтральной оси. Эти напряжения в зоне растяжения обозначаются +σ_max, а в зоне сжатия -σ_max.

29)В Брусе при изгибе возникает изги­бающий момент и поперечная сила.

правило знаков:

Внутренняя продольная сила N принимается положительной, в случае если она стремится растянуть отсеченную часть бруса.

Внутренний скручивающий момент T принимается положительным, если он стремится повернуть рассматриваемое сечение против хода часовой стрелки, при взгляде на него со стороны отброшенной части бруса.

Внутренняя поперечная сила Q принимается положительной, если она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

Внутренний изгибающий момент M принимается положительным, если он стремится сжать верхние слои бруса.

30) При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.

Рассмотрим для простоты балку с прямоугольным поперечным сечением (рис.6.9). Следуя методу сечений, мысленно проведем разрез и отбросим какую-либо часть балки, а другую оставим. На оставшейся части покажем действующие на нее силы и в поперечном сечении – внутренние силовые факторы, которые являются результатом приведения к центру сечения сил, действующих на отброшенную часть. Учитывая, что внешние силы и распределенные нагрузки лежат в одной плоскости и действуют перпендикулярно оси балки, в сечении получим поперечную силу и изгибающий момент . Эти внутренние силовые факторы заранее неизвестны, поэтому их показывают в положительном направлении в соответствии с принятыми правилами знаков.

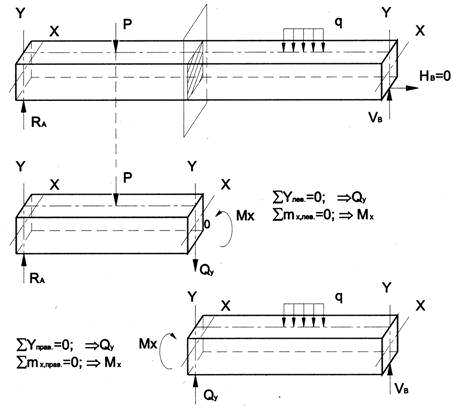
Рис.6.9

 

На рис.6.9 показаны два случая оставшейся части: левая и правая.

Для определения величины и составляются два уравнения равновесия для оставшейся части

Уравнение момента составляется относительно оси Х, проходящей в поперечном сечении через точку на оси балки – тогда поперечная сила в уравнение не входит и величина определяется независимо от . Можно доказать, что результат вычислений и не зависит от того, равновесие какой оставшейся части рассматривается.

Рассмотрим характерный пример (рис. 6.10,а) и установим не­обходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 6.10,б), выполняющими ту же роль, что и опорные закрепления.

Заданная система статически определима, следовательно, из ус­ловий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограниче­ний поворота сечений балки, поэтому изгибающих моментов не возникает) и , определяем вертикальные реакции в опорах:

.

Для определения имеем: откуда . Для проверки правильности вычислений воспользуемся усло­вием равенства нулю суммы всех вертикальных сил откуда получим

,     0 = 0.

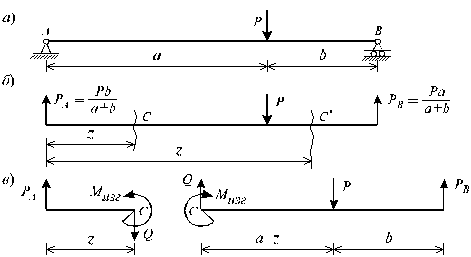
Рис. 6.10

Для определения внутренних силовых факторов  изгибающего момента М(z) и поперечной силы Q (z) как функций от продоль­ной координаты , воспользуемся методом сечений. Для полу­чения этих зависимостей балку разбивают на участки, границами которых являются следующие точки: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенных усилий; сечения, в которых скачкообразно изменя­ется жесткость балки; в точках, где происходит изменение ориен­тации элементов, если имеем дело с стержневой системой со сложной структурой.

Заданная система состоит из двух участков  первого и второго . Следовательно, задавая последовательно сечения, принадлежащие к первому и второму участкам, и рассмат­ривая равновесие отсеченных частей системы при действии на них всех внешних сил и внутренних уси­лий, определим выражения для внутренних сило­вых факторов.

Из условия равновесия ; отсеченной части системы, расположенной левее от сечения (первый участок), (см. рис. 6.10, в), получим:

;      .

Для определения и на втором участке рассмотрим рав­новесие отсеченной части балки, расположенной правее от сечения z₂ (см. рис. 6.10,б), т.е. ; откуда и определим:

;      .

Эпюры и изображены на рис. 6.11. Заметим, что эпюры изгибающих моментов , как и поперечных сил строятся на оси бруса, однако в отличие от эпюры поперечных сил знак момента не указывается, а ординаты изгибающего момента откла­дываются co стороны растянутых волокон.

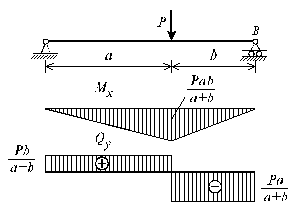
Рис. 6.11

31) 3. Контроль правильности построения эпюр с помощью правила Журавского

Из дифференциальных зависимостей Д. Журавского

следует, что на обоих незагруженных участках, где , эпюра перерезывающих сил постоянна , а эпюра изгибающих моментов – наклонная прямая линия. Так как на первом участке , то эпюра M_x с ростом z₁ возрастает. На втором участке , эпюра M_x с ростом должна убывать. Построенные эпюры полностью соответствуют правилам Д. Журавского. В сечении, где действует сосредоточенная сила , на эпюре Q_y имеет место скачок на соответствующую величину этой силы в ее направлении, а на эпюре M_x − излом, резкое изменение угла наклона.

32)  Нормальные напряжения зависят только от изгибающего момента, а касательные  только от поперечной силы. Это позволяет упростить  расчет нормальных напряжений для частного случая чистого изгиба, когда Q = 0. 

 Волокна, не изменяющие своей длины, образуют нейтральный слой. Линии пересечения нейтрального слоя с плоскостью сечения балки называется нейтральная ось.

 Расчет балок на прочность проводится по максимальным нормальным напряжениям, возникающим в тех поперечных сечениях, где наибольший изгибающий момент.

 Для балок из хрупких материалов составляют два условия прочности:

• для зоны растяжения:

• для зоны сжатия

Распределение нормальных нагрузок по сечению  таково, что часть материала, находящегося около нейтральной оси, почти не нагружена. Наиболее целесообразно использовать двухтавровое поперечное сечение, для которого с наименьшими затратами материала можно получить наибольший момент сопротивления.

33) При расчете на прочность элементов конструкций, работающих на изгиб, возможны три следующих вида задач, различающихся формой использования условия прочности (41.7):

а) проверка напряжений (проверочный расчет);

б) подбор сечения (проектный расчет);

в) определение допускаемой нагрузки (определение грузоподъемности).

Методика решения этих задач для балок из пластичных и хрупких материалов различна, так как балки из пластичных материалов одинаково работают на растяжение и сжатие, а из хрупких материалов лучше работают на сжатие, чем на растяжение. Это влияет на применяемые формы поперечных сечений балок и на способ определения опасного сечения.

Известные различия имеются также в расчетах балок постоянного по всей длине и переменного поперечного сечения.

Кроме того, следует иметь в виду, что в некоторых (сравнительно редких) случаях расчет на прочность только по наибольшим нормальным напряжениям, действующим в поперечном сечении балки, недостаточен, и приходится дополнительно производить проверку прочности также по главным напряжениям, возникающим в наклонных сечениях, и по максимальным касательным напряжениям.

Рассмотрим основные случаи расчетов на прочность при прямом изгибе.