- •Лабораторная работа №3. Опытная проверка закона Гука. Определение модуля упругости первого рода и коэффициента Пуассона.
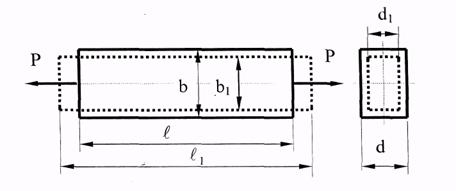
- •Изменение формы образца при испытаниях на растяжение
- •Универсальная машина ум-5
- •3) Разобраться со схемой рычажного тензометра и ознакомиться с реальным прибором (узнать, как он крепиться на деталь, как производится отсчет и т.П.).
- •Тензометр гуггенбергера рычажный
- •Форма отчета по лабораторной работе
- •Вопросы для подготовки к защите работы
Лабораторная работа №3. Опытная проверка закона Гука. Определение модуля упругости первого рода и коэффициента Пуассона.
Цель работы:
1. Проверить в пределах упругости линейность связи деформации и нагрузки.
2.
Определить числовые
значения упругих постоянных ![]() (модуля
упругости первого рода) и
(модуля
упругости первого рода) и ![]() (коэффициента
Пуассона) для стали.
(коэффициента
Пуассона) для стали.
3. Выяснить при этом физический смысл этих постоянных.
I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ:
1. Стальной образец прямоугольного поперечного сечения.
2. Разрывная машина с силоизмерительным устройством УМ-5.
3. Тензометр – прибор для измерения упругих удлинений.
4. Штангенциркуль.
П. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Упругие постоянные материалов используются при решении большого числа задач прочности и всех задач жёсткости и устойчивости. Они характеризуют способность материала сопротивляться различным видам деформаций при воздействии на них внешних нагрузок. Значения упругих характеристик, равно как и всех известных физических постоянных, не могут быть постулированы или найдены на основе логических и математических рассуждений, а могут быть получены только экспериментальным путём при испытании образцов на растяжение (сжатие), изгиб и кручение.
Различают материалы изотропные и анизотропные. Изотропия означает независимость свойств материала от направления воздействия нагрузки. Изотропные материалы характеризуются тремя упругими постоянными: модулем Юнга, коэффициентом Пуассона и модулем сдвига. При этом, как показывает теория, только две из них являются линейно независимыми. Анизотропные материалы могут иметь до 18 различных характеристик.
Монокристаллы и отдельные зёрна сталей анизотропны. Однако, благодаря их малости и хаотическому расположению в пространстве сталь приобретает статистически обоснованную изотропность и нуждается в экспериментальном определении, как минимум, двух упругих постоянных (например, модуля Юнга и коэффициента Пуассона).
Модуль
Юнга или модуль упругости первого
рода E характеризует
сопротивляемость материала деформированию
в направлении воздействия растягивающих
или сжимающих нагрузок. Чем больше
модуль Юнга, тем меньше удлинение или
укорочение стержня при прочих равных
условиях (длине, площади, нагрузке).
Модуль Юнга является коэффициентом
пропорциональности между нормальным
напряжением ![]() и
относительной линейной деформацией
и
относительной линейной деформацией ![]() в
законе Гука, записанном в дифференциальной
форме:
в
законе Гука, записанном в дифференциальной
форме: ![]() .
На основе этой формулы находят опытным
путём значение модуля упругости
.
На основе этой формулы находят опытным
путём значение модуля упругости
![]() , (1)
, (1)
где ![]() формула
для напряжения при растяжении,
подтверждённая теорией упругости
(эталоном точности для сопротивления
материалов) и опытными данными; F –
сила, растягивающая образец и определяемая
по силоизмерительному устройству; A –площадь
поперечного сечения, определяемая путём
измерения размеров;
формула
для напряжения при растяжении,
подтверждённая теорией упругости
(эталоном точности для сопротивления
материалов) и опытными данными; F –
сила, растягивающая образец и определяемая
по силоизмерительному устройству; A –площадь
поперечного сечения, определяемая путём
измерения размеров; ![]() относительная
продольная деформация, определяемая
методом тензометрирования.
относительная
продольная деформация, определяемая
методом тензометрирования.
На
основании закона Гука (1) абсолютная
продольная деформация бруса ![]() прямо
пропорциональна внутренней продольной
силе
прямо
пропорциональна внутренней продольной
силе ![]() ,
вызвавшей эту деформацию:
,
вызвавшей эту деформацию:
![]() . (2)
. (2)
Измерив опытным путем величину осевой нагрузки F и вызванную ею продольную деформацию и зная размеры испытуемого бруса, вычисляют модуль продольной упругости по формуле, полученной из (2)
![]() . (3)
. (3)
Геометрические
параметры образца ![]() и A находятся
до нагружения, а нагрузка и соответствующее
ей удлинение берутся из опыта.
и A находятся
до нагружения, а нагрузка и соответствующее
ей удлинение берутся из опыта.
Коэффициент
Пуассона
характеризует
способность материала сопротивляться
поперечному деформированию, т.е. изменению
размеров в направлении, перпендикулярном
воздействию силы. Это сопротивление
французский академик Пуассон предложил
характеризовать в безразмерной форме
как модуль отношения поперечной ![]() и
продольной
относительных
деформаций, определяемых опытным путём:
и
продольной
относительных
деформаций, определяемых опытным путём:
![]() .
.
где ![]() ;
;
b и l - начальные поперечные и продольные размеры бруса, соответственно.
Для
нахождения ![]() ' и
достаточно
при одной и той же нагрузке измерить
абсолютное сужение
' и
достаточно
при одной и той же нагрузке измерить
абсолютное сужение ![]() и
абсолютное удлинение
и
абсолютное удлинение ![]() ,
а также знать необходимые первоначальные
размеры.
,
а также знать необходимые первоначальные
размеры.