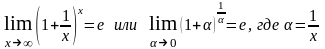- •Раздел 2. Основы математического анализа.
- •Тема 2.1 Функции одной независимой переменной (повторение).
- •2.1.1. Основные понятия.
- •2.1.2. Способы задания функции
- •2.1.3. Основные свойства функций. Четность и нечетность функций.
- •Тема 2.2 Предел и непрерывность функций (повторение).
- •2.2.1. Основные понятия.
- •2.2.2. Бесконечно большие и бесконечно малые функции.
- •2.2.3. Основные теоремы о пределах.
- •2.2.4. Сравнение бесконечно малых функций.
- •2.2.5. Определение непрерывности функции в точке.
- •2.2.6. Техника вычисления пределов.
- •Тема 2.3 Производная функции (повторение).
- •2.3.1.Основные понятия Определение производной
- •Общепринятые обозначения производной функции
- •Правила дифференцирования
- •2.3.2. Производная сложной функции
- •2.3.3.Таблица производных функций независимой переменной.
- •2.3.4. Таблица производных функций, аргументом которой является функция.
- •2.3.5. Логарифмическое дифференцирование
- •2.3.6. Производная степенно-показательной функции
- •2.3.7. Производные высшего порядка
Тема 2.2 Предел и непрерывность функций (повторение).
2.2.1. Основные понятия.
Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию.
Определение предела по Коши. Число A называется пределом функции f(x) в точке x0, если эта функция определена в некоторой окрестности точки x0 за исключением, быть может, самой точки x0, и для каждого ε>0 существует δ>0 такое, что для всех x, удовлетворяющих условию |x–x0|<δ, x≠x0, выполняется неравенство |f(x)–A|<ε.
Определение предела по Гейне. Число
A называется пределом функции
f(x) в точке
x0,
если эта функция определена в некоторой
окрестности точки x0
за исключением, быть может, самой точки
x0,
и для любой последовательности
 такой, что
такой, что
 сходящейся к числу x0,
соответствующая последовательность
значений функции
сходящейся к числу x0,
соответствующая последовательность
значений функции
 сходится к числу A.
сходится к числу A.
Если A – предел функции в точке
x0,
то пишут, что

Если функция f(x) имеет предел в точке х0, то этот предел единственный.
Число A1 называется
пределом функции f(x)
слева в точке х0,
если для каждого ε>0 существует
δ>0 такое, что для всех
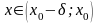 выполняется неравенство
выполняется неравенство

Число A2 называется
пределом функции f(x)
справа в точке х0,
если для каждого ε>0 существует
δ>0 такое, что для всех
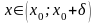 выполняется неравенство
выполняется неравенство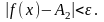
Предел слева обозначается
 предел справа –
предел справа –
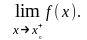
Эти пределы характеризуют поведение функции слева и справа от точки х0. Их часто называют односторонними пределами
Предел функции на бесконечность.
Пусть функция f(x) определена на (-, + ∞).
Число A называется пределом
функции f(x) при x → ∞ , если
для любого положительного числа
существует такое число М>0, что при
всех х, удовлетворяющих условию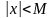 ,
выполняется неравенство
,
выполняется неравенство

2.2.2. Бесконечно большие и бесконечно малые функции.
Функция
y=f(x)
называется бесконечно
малой
при x→х0
или
при x→∞,
если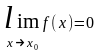 или
или ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
Функция
y=f(x)
называется бесконечно
большой
при x→х0
или
при x→∞,
если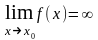 или
или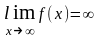 ,
т.е. бесконечно большая функция – это
функция, предел которой в данной точке
равен бесконечности.
,
т.е. бесконечно большая функция – это
функция, предел которой в данной точке
равен бесконечности.
Теорема. Если f (x) —
бесконечно большая функция, то
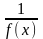 есть
бесконечно малая функция в этой же
точке.
есть
бесконечно малая функция в этой же
точке.
2.2.3. Основные теоремы о пределах.
Эти свойства выражают правила, по которым можно находить пределы функций. Они называются правилами предельного перехода.
Теорема 1 (о пределе алгебраической суммы). Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
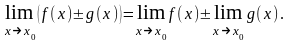
Теорема 2 (о пределе произведения). Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций, т.е.

Следствие 1. Постоянный множитель можно выносить за знак предела:
 .
.
Следствие 2. Предел степени равен степени предела:
 .
.
Теорема 3 (о пределе частного). Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
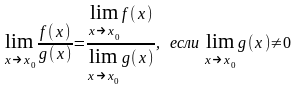
Все теоремы справедливы и при
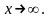
Замечательные пределы.
Первый замечательный предел:
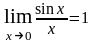
Второй замечательный предел: