Раздел 2. Основы математического анализа.

Группа	Дата
ОП-253	07.02.2014
ОП-254	07.02.2014

Тема 2.1 Функции одной независимой переменной (повторение).

2.1.1. Основные понятия.

Пусть даны два непустых подмножества D и Е множества R. Если каждому элементу х из D сопоставляется по какому - либо правилу один и только один элемент у из Е, то говорят, что на множестве D задана функция. Эта функция записывается в виде

y = f (x), где x D или x → f (x), где x D

Подмножество D или D (f) называется областью определения функции у = f (х), подмножество Е или Е (f) множеством ее значений.

Переменная х называется независимой переменной или аргументом, переменная y - зависимой переменной или значением функции.

Для того чтобы задать функцию f, нужно указать:

1) ее область определения D (f );

2) указать правило f, по которому каждому значению хD ставится в соответствие некоторое значение y = f (x).

Если множество D специально не оговорено, то под областью определения функции понимают область допустимых значений аргумента х, т.е. множество таких значений х, при которых функция y = f (x) вообще имеет смысл.

Замечание. Для обозначения функции не обязательно использовать буквы х и у. Так, например, каждому значению радиуса шара R соответствует одно значение объема шара: 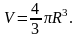Следовательно, объем шара является функцией радиуса шара. Областью определения этой функции является множество , так как радиус шара не может быть отрицательным. Множество значений , так как объем шара не может быть отрицательным.

2.1.2. Способы задания функции

Аналитическое задание функции. Функция задана аналитически, если функциональная зависимость выражена в виде формулы, которая указывает совокупность тех математических операций, которые должны быть выполнены, чтобы по данному значению аргумента найти соответствующее значение функции. Если функция задана формулой, то при отсутствии особых оговорок областью ее определения считается наибольшее множество, на котором эта формула имеет смысл.

Графический способ задания функции. Графиком числовой функции у = f (х) называется множество точек плоскости с координатами (х; f (х)), абсциссы которых - числа из области определения функции, а ординаты - соответствующие значения функции, т. е.

Г = {(x; y)| xD , y = f (х)}.

Графический способ задания функции используют тогда, когда функцию трудно или невозможно задать аналитически. График функции дает наглядное представление о свойствах функции. Задать функцию графически - это значит построить ее график

При табличном способе задания функции рядом с числовым значением аргумента выписывается соответствующее значение функции. Таблицы могут составляться также по значениям х и у, полученным из опыта или наблюдения. Недостатком табличного способа задания функции является то, что в таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции.

Словесный способ использует естественный язык для описания функциональной зависимости.