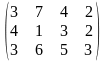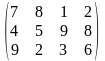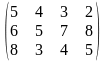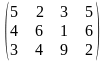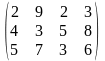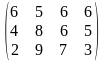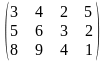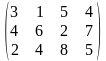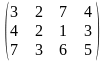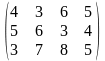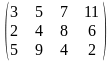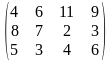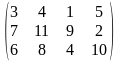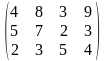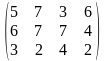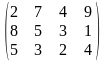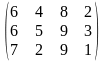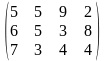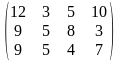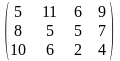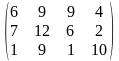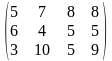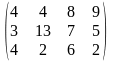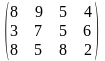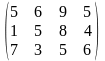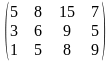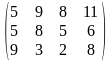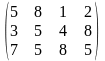1.6.3 Транспортная задача.

Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования.

Транспортная задача делится на два вида: транспортная задача по критерию стоимости – определение плана перевозок, при котором стоимость груза была бы минимальна; транспортная задача по критерию времени – более важным является выигрыш по времени.

Задача заключается в отыскании такого плана перевозок продукции с m складов в n пунктов назначения, который потребовал бы минимальных затрат. Если потребитель j 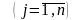получает единицу продукции (по прямой дороге) со склада i 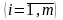то возникают издержки C_ij. Предполагается, что транспортные расходы пропорциональны перевозимому количеству продукции, т.е. перевозка k единиц продукции вызывает расходы kС_ij. Далее, предполагается, что 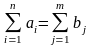, где a_i есть количество продукции, находящееся на складе i, и b_j – потребность потребителя j. Такая транспортная задача называется закрытой. Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребностей, имеет решение.

Составление опорного плана Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы. Например, способ северо-западного угла, способ минимальной стоимости по строке, способ минимальной стоимости по столбцу и способ минимальной стоимости таблицы. Рассмотрим простейший, так называемый способ северо-западного угла. Пояснить его проще всего будет на конкретном примере. Условия транспортной задачи заданы транспортной таблицей: Таб.1

	Потребитель						Запасы а_i
Поставщик	В₁	В₂	В₃	В₄	В₅
А₁	10	8	5	6	9	48
А₂	6	7	8	6	5	30
А₃	8	7	10	8	7	27
А₄	7	5	4	6	8	20
Заявки b_j	18	27	42	12	26	125

Введенная таблица дает нам следующую информацию:

Запасы однотипной продукции, которая находится у поставщиков A₁, A₂, A₃, А₄.
Потребность в однотипной продукции потребителей B₁, B₂, B₃, B₄,В₅.
Стоимость доставки единицы продукции от каждого поставщика к каждому потребителю (тарифы маршрутов).
Суммарные запасы продукции у поставщиков равняются суммарной потребности потребителей, следовательно, задача является закрытой.

Найдем начальное решение методом северо-западного угла.

Будем заполнять таблицу перевозками постепенно, начиная с левой верхней ячейки ("северо-западного угла" таблицы). Будем рассуждать при этом следующим образом. Пункт В₁подал заявку на18 единиц груза. Удовлетворим эту заявку за счёт запаса 48, имеющегося в пункте А₁ , и запишем перевозку 18 в клетке (1,1). После этого заявка пункта В₁удовлетворена, а в пункте А₁ осталось ещё 30 единиц груза. Удовлетворим за счёт них заявку пункта В₂ (27 единиц), запишем 27 в клетке (1,2); оставшиеся 3 единицы пункта А₁ назначим пункту В₃. В составе заявки пункта В₃ остались неудовлетворёнными 39 единиц. Из них 30 покроем за счёт пункта А₂, чем его запас будет исчерпан, и ещё 9 возьмём из пункта А₃. Из оставшихся 18 единиц пункта А₃ 12 выделим пункту В₄; оставшиеся 6 единиц назначим пункту В₅, что вместе со всеми 20 единицами пункта А₄ покроет его заявку. На этом распределение запасов закончено; каждый пункт назначения получил груз, согласно своей заявке. Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запасу, а в столбце - заявке. Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи:

Таб.2

	Потребитель																		Запасы а_i
Поставщик	В₁		В₂			В₃				В₄				В₅
А₁	10			8			5					6				9					48
		18			27				3
А₂	6		7			8					6				5					30
								30
А₃	8		7			10					8				7					27
								9					12					6
А₄	7		5			4				6				8					20
																	20
Заявки b_j	18		27			42				12				26					125

Вычислим затраты:

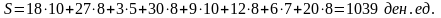
Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок С_ij . Другой способ - способ минимальной стоимости по строке - основан на том, что мы распределяем продукцию от пункта A_i не в любой из пунктов B_j, а в тот, к которому стоимость перевозки минимальна. Если в этом пункте заявка полностью удовлетворена, то мы убираем его из расчетов и находим минимальную стоимость перевозки из оставшихся пунктов B_j. Во всем остальном этот метод схож с методом северо-западного угла. В результате, опорный план составленный способом минимальной стоимости по строке выглядит, так как показано в таблице. Таб.3

	Потребитель																Запасы а_i
Поставщик	В₁		В₂		В₃		В₄				В₅
А₁	10		8		5			6					9						48
						42				6
А₂	6		7		8		6				5					30
		4												26
А₃	8		7		10		8				7						27
				27											0
А₄	7		5		4		6					8						20
		14							6
Заявки b_j	18		27		42		12				26						125

Вычислим затраты:

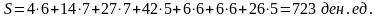
При этом методе может получиться, что стоимости перевозок C_ij и C_ik от пункта A_i к пунктам B_j и B_k равны. В этом случае, с экономической точки зрения, выгоднее распределить продукцию в тот пункт, в котором заявка больше. Так, например, в строке 2: C₂₁ = C₂₄, но заявка b₁ больше заявки b₄, поэтому 4 единицы продукции мы распределим в клетку (2,1).

Способ минимальной стоимости по столбцу аналогичен предыдущему способу. Их отличие состоит в том, что во втором способе мы распределяем продукцию от пунктов B_i к пунктам A_j по минимальной стоимости C_ji. Опорный план, составленный способами минимальных стоимостей, обычно более близок к оптимальному решению. Так в нашем примере общие затраты на транспортировку по плану, составленному первым способом S = 1039, а по второму S= 723.

Клетки таблицы, в которых стоят ненулевые перевозки, являются базисными. Их число должно равняться m + n - 1 Необходимо отметить также, что встречаются такие ситуации, когда количество базисных клеток меньше чем m + n - 1. В этом случае распределительная задача называется вырожденной. И следует в одной из свободных клеток поставить количество перевозок равное нулю. Так, например, в таб.3: m + n - 1 = 4 + 5 - 1 = 8, а базисных клеток 7, поэтому нужно в одну из клеток строки 3 или столбца 2 поставить значение “0”. Например в клетку (3,5). Составляя план по способам минимальных стоимостей в отличии от плана по способу северо-западного угла мы учитываем стоимости перевозок C_ij, но все же не можем утверждать, что составленный нами план является оптимальным.

Задание для практической работы №1(часть 3)

Поставщики А₁, А₂, А₃ имеют а₁, а₂, а₃единиц однородного груза. Потребность в однородной продукции потребителей В₁, В₂, В₃, В₄ составляет соответственно в₁, в₂, в₃, в₄единиц. Стоимость перевозки (тариф маршрута) единиц груза от поставщика к потребителю задается матрицей. Сравнить суммарные затраты по перевозке груза, вычисленные способом северо-западного угла и способом минимальной стоимости по строке.

Значения а₁, а₂, а₃, в₁, в₂, в₃, в₄, а матрицы находятся по таблице.

Вариант	Поставщики			Потребители				Тариф маршрутов
	А₁	А₂	А₃	В₁	В₂	В₃	В₄
	а₁	а₂	а₃	в₁	в₂	в₃	в₄
1	40	180	300	60	100	220	140
2	200	180	190	150	130	150	140
3	150	180	300	90	120	200	220
4	90	230	120	100	120	80	140
5	100	85	130	60	135	90	30
6	60	80	100	50	70	100	20
7	230	160	60	120	80	130	120
8	80	95	135	20	35	100	155
9	200	90	130	80	110	110	120
10	30	60	280	250	60	140	190
11	17	32	89	9	12	67	50
12	48	34	89	30	45	53	43
13	85	123	98	105	87	79	35
14	140	97	78	50	93	84	88
15	120	96	180	84	124	96	92
16	160	98	132	65	112	96	117
17	20	55	78	40	42	35	36
18	35	80	16	46	12	50	23
19	110	150	160	200	105	60	55
20	58	34	89	30	45	63	43
21	130	97	58	70	93	84	78
22	160	85	275	190	115	200	125
23	105	95	145	45	35	110	155
24	64	84	153	120	34	120	27
25	145	76	292	112	109	250	42
26	210	195	190	90	110	115	285
27	35	55	178	40	92	85	51
28	160	98	232	115	162	96	117
29	100	85	230	60	135	190	30
30	158	34	89	80	45	63	93