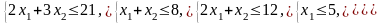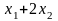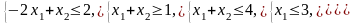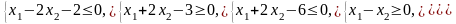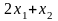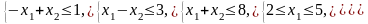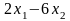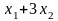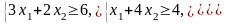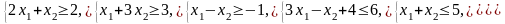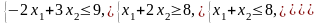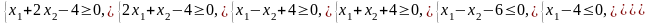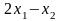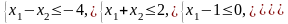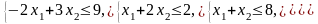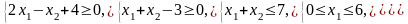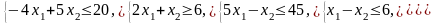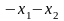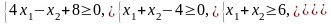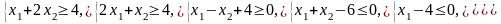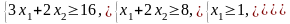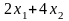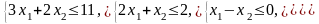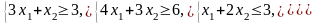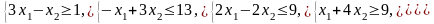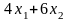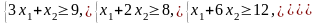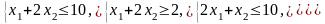1.6.2 Графический метод решения задачи линейного программирования.

Напоминаю, если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если задача содержит только две переменные, то ее можно решить графически.

Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция 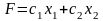принимает максимальное (или минимальное) значение.

Рассмотрим так называемую линию уровня линейной функции F , т.е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение а, т.е.

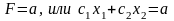
Уравнение линии уровня есть уравнение прямой линии. При различных уровнях а линии уровня параллельны.

усть графическим изображением системы ограничений является многоугольник ABCDE:

Важное свойство линии уровня состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – только убывает.

Для определения направления возрастания рекомендуется изобразить две линии уровня и определить, на которой из них уровень больше.

Для нахождения среди точек многоугольника такой, в которой линейная функция принимает максимальное (или минимальное) значение, можно поступить иначе: найти координаты всех вершин многоугольника, как точек пересечения прямых; вычислить значения целевой функции в каждой точке и выбрать среди этих значений максимальное (или минимальное).

Примеры.

а) Найти максимум целевой функции при заданных ограничениях:

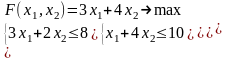
Решение.

На плоскости возьмем систему координат и построим допустимое множество D, которое представляет собой область, ограниченную линиями, определяемыми из условия задачи (как это сделать – смотри выше п. 1.5.2):

Неравенству 3х₁+2х₂  8 удовлетворяют точки полуплоскости, и граница этой полуплоскости есть прямая линия х₂= 4-1,5 х₂ . Проще всего эту прямую построить по точкам пересечения ее с осями координат. Это точки (0,4) и (8/3,0). Чтобы узнать нужную полуплоскость, надо подставить в неравенство 3х₁+2х₂  8 координаты какой-нибудь точки, не лежащей на прямой, например О(0,0). Неравенство верно, значит, искомой полуплоскостью является та, в которой находится точка О(0,0). Аналогично поступаем со вторым ограничением. Получаем вторую полуплоскость.

Неотрицательность каждой переменной задает первую координатную четверть. Пересечение всех четырех полуплоскостей дает искомое допустимое множество – четырехугольник ОАВС.

Теперь на нем надо найти максимум целевой функции F(x₁,x₂). Он достигается в какой-то из угловых точек О, А, В или С. Координаты точек несложно определить О(0,0), А(0;2,5), С(8/3,0). Для нахождения координат точки В надо решить систему двух уравнений:

Вычислим значения целевой функции в этих точках:F(0)=0, F(A)= 10, F(B)=12,4, F(C)=8.

Отсюда видно, что максимум равен 12,4 и достигается он в точке В(1,2;2,2).

в) Решим задачу в) из п.6.1.1, математическая модель которой уже построена, т.е. необходимо найти минимум целевой функции при заданных ограничениях:

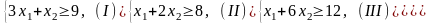
Решение.

По расположению линии уровня, например, F=12 или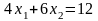 (прямую можно построить по точкам, взяв, например, сначала х₁=0, получим х₂=2 и точку (0;2), затем х₂=0 и х₁=3 – точка (3;0)), находим направление вектора 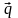. Очевидно, что точка минимума – это точка В «входа» в многоугольник решений, ибо при дальнейшем перемещениилинии уровня в направлении вектора значения линейной функции увеличиваются. Найдем координаты точки В, как точки пересечения прямых II и III.

ногоугольник допустимых значений представляет собой неограниченную многоугольную область.

III

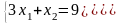
_{Подставляя координаты точки В в
целевую функцию получаем:}

Итак, F_min=26 при оптимальном решении х₁=2, х₂=3, т.е. минимальная стоимость рациона 26 руб., если в него включить 2 единицы корма А и 3 единицы корма В.

Задание для практической работы №1(часть 2)

Найти максимум целевой функции F(x₁,x₂) и минимум целевой функции G(x₁,x₂) при заданных ограничениях

Вариант	F(x₁,x₂)	Ограничения	Вариант	G(x₁,x₂)	Ограничения
1			2
3			4
5			6
7			8
9			10
11			12
13			14
15			16
17			18
19			20
21			22
23			24
25			26
27			28
29			30