- •Раздел 1. Линейная алгебра.
- •Тема 1.5 Системы линейных неравенств с двумя переменными.
- •1.5.1 Основные понятия. Неравенства с двумя переменными.
- •1.5.2. Системы линейных неравенств.
- •Тема 1.6 Простейшие задачи линейного программирования.
- •1.6.1 Постановка задачи линейного программирования (лп).
- •1.6.2 Графический метод решения задачи линейного программирования.
- •1.6.3 Транспортная задача.
1.6.1 Постановка задачи линейного программирования (лп).
В общем виде задача линейного
программирования ставится следующим
образом: найти переменные
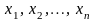 удовлетворяющие
системе неравенств (уравнений):
удовлетворяющие
системе неравенств (уравнений):
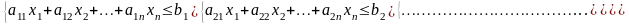
и обращающие в максимум
(или минимум) функцию: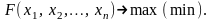
Переменные называются управляющими переменными или решениями задачи;
Коэффициенты
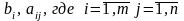 - параметры;
- параметры;
Система неравенств называется ограничением задачи;
Функция
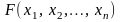 целевая
функция или критерий эффективности
задачи;
целевая
функция или критерий эффективности
задачи;
Решение задачи
 ,
при котором целевая функция задачи
принимает свое максимальное (минимальное)
значение, называется оптимальным.
,
при котором целевая функция задачи
принимает свое максимальное (минимальное)
значение, называется оптимальным.
Множество всех допустимых решений задачи линейного программирования представляет собой выпуклый многогранник или выпуклую многогранную область, которая называется многогранником решений.
Теорема. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений.
В зависимости от вида целевой функции и ограничений можно выделить несколько типов задач линейного программирования или линейных моделей: общая линейная задача, транспортная задача, задача о назначениях.
Примеры.
а) Для изготовления трех видов изделий А, В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида.
Тип оборудования |
Затраты времени (станко-часы) на обработку одного изделия каждого вида |
Общий фонд рабочего времени оборудования (часы) |
|||
А |
В |
С |
|||
Фрезерное |
2 |
4 |
5 |
120 |
|
Токарное |
1 |
8 |
6 |
280 |
|
Сварочное |
7 |
4 |
5 |
240 |
|
Шлифовальное |
4 |
6 |
7 |
360 |
|
Прибыль (руб.) |
10 |
14 |
12 |
|
|
Требуется определить, сколько изделий, и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Составить математическую модель задачи.
Решение.
Предположим, что будет изготовлено
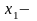 единиц
изделий вида А,
единиц
изделий вида А,
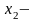 единиц
изделий вида В,
единиц
изделий вида В,
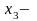 единиц изделий вида С.
единиц изделий вида С.
Тогда прибыль от их реализации составит
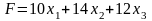
Для производства такого количества
изделий потребуется затратить
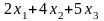 станко-часов
фрезерного оборудования.
станко-часов
фрезерного оборудования.
Так как общий фонд рабочего времени
станков данного типа не может превышать
120, то должно выполняться неравенство
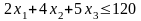 .
.
Аналогичные рассуждения относительно возможного использования токарного, сварочного и шлифовального оборудования приведут к следующим неравенствам:
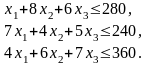
При этом, так как количество изготовляемых изделий не может быть отрицательным, то
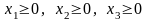
Таким образом, приходим к следующей математической задаче:
дана система четырех линейных
неравенств с тремя неизвестными
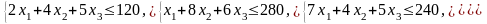
и линейная функция относительно этих же переменных .
Требуется среди всех неотрицательных
решений системы неравенств найти такое,
при котором функция принимает максимальное
значение, т.е.
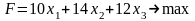
Линейная функция, максимум которой требуется определить, вместе с системой неравенств и условием неотрицательности переменных образуют математическую модель исходной задачи.
Так как функция линейная, а система содержит только линейные неравенства, то задача является задачей линейного программирования.
б) Имеется два вида корма А
и В, содержащие питательные вещества
 Содержание
числа единиц питательных веществ в 1 кг
каждого вида корма и необходимый минимум
питательных веществ приведены в таблице
(цифры условные).
Содержание
числа единиц питательных веществ в 1 кг
каждого вида корма и необходимый минимум
питательных веществ приведены в таблице
(цифры условные).
Питательное вещество |
Необходимый минимум питательных веществ |
Число единиц питательных веществ в 1 кг корма |
|
А |
В |
||
|
9 |
3 |
1 |
|
8 |
1 |
2 |
|
12 |
1 |
6 |
Стоимость 1 кг корма А и В соответственно равна 4 руб. 6 руб.
Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.
Решение.
Обозначим
количество корма вида А, входящего в дневной рацион,
количество корма вида В, входящего в дневной рацион.
Тогда этот рацион будет включать:
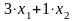 единиц
питательного вещества
единиц
питательного вещества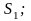
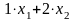 единиц
питательного вещества
единиц
питательного вещества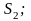
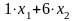 единиц
питательного вещества
единиц
питательного вещества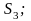
Так как содержание питательных веществ
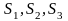 в
рационе должно быть не менее соответственно
9, 8 и 12 единиц, то получим систему
неравенств – ограничений:
в
рационе должно быть не менее соответственно
9, 8 и 12 единиц, то получим систему
неравенств – ограничений:
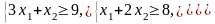
При этом, так как количество корм не может быть отрицательным, то
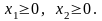
Общая стоимость рациона составит (в руб.):
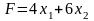
Экономико-математическая модель задачи:
Составить дневной рацион
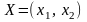 ,
удовлетворяющий системе неравенств –
ограничений и условию неотрицательности
переменных, при котором функция
,
удовлетворяющий системе неравенств –
ограничений и условию неотрицательности
переменных, при котором функция
принимает
минимальное значение, т.е.