Раздел 1. Линейная алгебра.

Группа	Дата
ОП-253	31.01.2014, 05.02.2014
ОП-254	29.01.2014, 31.01.2014

Тема 1.5 Системы линейных неравенств с двумя переменными.

1.5.1 Основные понятия. Неравенства с двумя переменными.

Принципиальное отличие неравенств с двумя переменными от неравенств с одной переменной состоит в размерности. Если при решении неравенств с одной переменной мы имеем числовую ось, т.е. существуют только «иксы», то сейчас добавляются «игреки» и поле деятельности расширяется до всей координатной плоскости.

Помимо аналитической геометрии, материал актуален для ряда задач математического анализа, экономико-математического моделирования.

Различают два типа линейных неравенств:

1) Строгие неравенства:

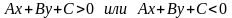
2) Нестрогие неравенства:

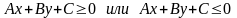
Геометрический смысл этих неравенств состоит в следующем:

если линейное уравнение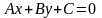 задаёт прямую, то линейное неравенство определяет полуплоскость.

Как известно, ось абсцисс ОХ задаётся уравнением 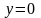– «игрек» всегда (при любом значении «икс») равняется нулю

Рассмотрим неравенство 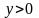. «Игрек» всегда (при любом значении «икс») положителен. Очевидно, что данное неравенство определяет верхнюю полуплоскость – ведь там и находятся все точки с положительными «игреками».

В том случае, если неравенство нестрогое 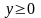, к верхней полуплоскости дополнительно добавляется сама ось OX.

Аналогично: нерав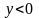енству удовлетворяют все точки нижней полуплоскости, нестрогому неравенству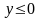 соответствует нижняя полуплоскость «плюс» ось OX.

С осью ординат OY то же самое:

– неравенство 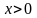задаёт правую полуплоскость;

– неравенство 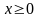задаёт правую полуплоскость, включая ось ординат;

– неравенство  задаёт левую полуплоскость;

– неравенство 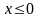  задаёт левую полуплоскость, включая ось ординат.

Рассмотрим неравенства, в которых отсутствует одна из переменных.

1. Отсутствует «игрек»:

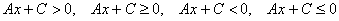
2. Отсутствует «икс»:

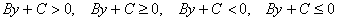
Решить линейное неравенство – это значит найти полуплоскость, точки которой удовлетворяют данному неравенству (плюс саму прямую, если неравенство нестрогое). Решение, как правило, графическое и состоит в следующем:

_{1. П}остроить прямую

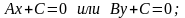
_{для удобства построения целесообразно выразить из уравнения переменную:}

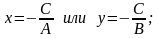
_{2. Выбрать любую точку плоскости, не принадлежащую построенной прямой. (как правило, это начало координат – точка с координатами О(0;0));}

_{3. Подставить координаты выбранной точки в исходное неравенство;}

– Если какая-либо точка полуплоскости (не принадлежащая прямой) не удовлетворяет неравенству, то и ВСЕ точки данной полуплоскости не удовлетворяют данному неравенству.

– Если какая-либо точка полуплоскости (не принадлежащая прямой) удовлетворяет неравенству, то и ВСЕ точки данной полуплоскости удовлетворяют данному неравенству.

Примеры.

а) Решить неравенство

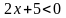
Решение.

Чертим прямую

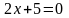
выразив из уравнения переменную 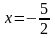. Прямая изображается пунктирной линией, так как неравенство «строгое» и точки прямой не являются его решением

Теперь выбираем любую точку плоскости, не принадлежащую прямой. Выберем начало координат, точку (0;0). Она лежит в правой полуплоскости от начерченной прямой. Подставим координаты данной точки в неравенство:

Получено неверное неравенство.

Следовательно, неравенству удовлетворяют точки, лежащие в левой полуплоскости от прямой. Решение изображается стрелочками либо штрихуется.

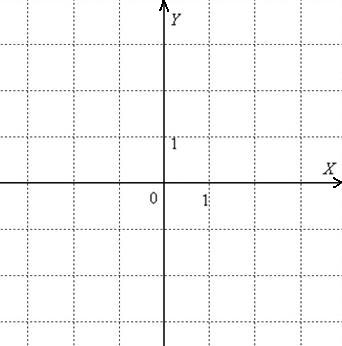
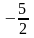
_{б) Решить} неравенство

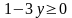
Решение

Чертим прямую

выразив из уравнения переменную 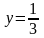. Прямая изображается сплошной линией, так как неравенство «нестрогое» и точки прямой являются его решением.

Теперь выбираем любую точку плоскости, не принадлежащую прямой. Выберем начало координат, точку (0;0). Она лежит в нижней полуплоскости от начерченной прямой. Подставим координаты данной точки в неравенство:

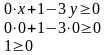
Получено верное неравенство.

Следовательно, неравенству удовлетворяют все точки, лежащие в нижней полуплоскости от прямой. Решение изображается стрелочками либо штрихуется.

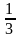
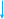
Переходим к рассмотрению третьего, общего случая, когда в неравенстве присутствуют обе переменные:

Решение графическое:

_{1. Построить прямую}

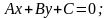
_{для удобства построения целесообразно выразить из уравнения переменную y:}

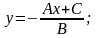
_{2. Выбрать любую точку плоскости, не принадлежащую построенной прямой. (как правило, это начало координат – точка с координатами О(0;0));}

_{3. Подставить координаты выбранной точки в исходное неравенство;}

– Если какая-либо точка полуплоскости (не принадлежащая прямой) не удовлетворяет неравенству, то и ВСЕ точки данной полуплоскости не удовлетворяют данному неравенству.

– Если какая-либо точка полуплоскости (не принадлежащая прямой) удовлетворяет неравенству, то и ВСЕ точки данной полуплоскости удовлетворяют данному неравенству.

Пример.

а) Найти полуплоскости, соответствующие неравенству

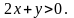
Решение

Чертим прямую

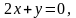
выразив из уравнения переменную 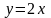. Прямая изображается пунктирной линией, так как неравенство «строгое» и точки прямой не являются его решением.

Теперь выбираем любую точку плоскости, не принадлежащую прямой. Начало координат выбрать нельзя, т.к. оно принадлежит прямой. Выберем точку с небольшими координатами, например, М(1;0). Подставим координаты данной точки в неравенство:

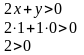
Получено верное неравенство.

Следовательно, неравенству удовлетворяют точки полуплоскости, в которой находится точка М. Решение изображается стрелочками либо штрихуется.

М(1;0)

∙