2.2 Тербелмелі-станок балансирінің басына түсетін жүктемені анықтау

2.2.1-кесте - Бастапқы берілгендер

Берілгендер	Белгіленуі	Мәндері
сораптың ілу тереңдігі, м	L	900
динамикалық деңгей, м	h	850
плунжер диаметрі, мм	Dтығ	55
штанга диаметрі, мм	dш1	25
штанга диаметрі, мм	dш2	22
штангалар секциясының ұзындығы, м	L1	378
штангалар секциясының ұзындығы, м	L2	522
сұйықтың тығыздығы, кг/м3	ρс	850

(2.2.1) формула бойынша Коши параметрін анықтаймыз:

µ=ωL/а, (2.2.1)

мұндағы L-сораптың ілу тереңдігі;

а-штангадағы дыбыс жылдамдығы, екісатылы тізбек үшін а=4900 м/с;

ω=1,26 с^-1.

µ=1,26·900/4900=0,231.

Динамикалық режим сәйкесінше динамикалық теория формулалары бойынша дұрыс жүктемені береді.

1. Статикалық теория. (2.2.2) формуласымен Р_б=0 деп алып, плунжер үстіндегі сұйықтық бағанының салмағын есептейміз:

Р_с=F_пл(h_дρ_cg+Р_б), (2.2.2)

Р_с=0,785·0,055²·850·850·9,8=16814 H.

Сұйықтағы штанганың жеңілдету коэффициенті:

b= , (2.2.3)

b= =0,89.

Динамикалық фактор:

m= , (2.2.4)

мұндағы S_A -штанганың ілу нүктесінің жүру ұзындығы, S_A=3,5 м;

n- бір минуттағы тербеліс саны, СК8-3,5-6000 үшін, n_max=12 мин^-1.

m= =0,35.

Ауадағы штанга салмағын анықтаймыз:

Р_ш=(q₁L₁+q₂L₂)g, (2.2.5)

Р_ш =(4,1·378+3,14·522)9,81=31283 H.

Статикалық теория бойынша максималды жүктемені И.М.Муравьев формуласы бойынша анықтаймыз:

Р_max=P_c+P_ш(b+m), (2.2.6)

Р_max=16814+31283(0,89+0,35)=55605 H.

Минималды жүктемені (2.2.7) формуласымен анықтаймыз:

P_min=P_ш(b-m), (2.2.7)

P_min=31283(0,89-0,35)=16893 H.

2. А.С.Вирновский формулалары.

Сұйықтағы штанга тізбегінің салмағын анықтаймын:

Р_шт'= Р_ш[1 – ρ_c/ ρ_ш]= Р_ш·b, (2.2.8)

Р_шт'=31283·0,89=27842 Н.

Штанганың көлденең қималарының аудандары. Егер есеп сатылы тізбек үшін жүргізілетін болса, онда ƒ_шт орнына мынаны алу керек:

, (2.2.9)

мұндағы ε₁......ε_n - екісатылы штанга тізбегінің үлестері, ∑ε₁=1.

Штангалардың орташа диаметрі келесідей анықталады:

м. (2.2.10)

Сақиналы кеңістіктегі сұйықтық бағанының салмағын есептеймін:

Р_с΄ =(Ғ_пл – ƒ_шт.орт)ρ_сgL, (2.2.11)

Р_с'= 0,785(0,055²-d²_шт.орт)850·9,81·900=

=(23,75-4,2)10^-4·850·9,81·900=14672 Н.

Сұйықтық бағанының салмағына байланысты штанганың ұзаруын есептейміз:

, (2.2.12)

Сораптан құбырға ауысқан кездегі сұйықтың қимасының өзгеру коэффициенті:

, (2.2.13)

мұндағы Ғ_құб – құбырдың ішкі каналының ауданы; Ғ_құб =0,785·0,051²=20,42·10^-4 м;

плунжердің көлденең қималарының аудандары.

.

Аудандардың қатынас коэффициенті:

, (2.2.14)

мұндағы ƒ_құб-металл бойынша құбыр қимасының ауданы. ƒ_құб =0,785(0,06²-0,051²)=7,84·10^-4 м;

СК-8-3,5-6000 станогы үшін S_A=3,5 м [4] болғанда α₁=1,10; a₁=0,9; α₂=0,73; а₂=1,56 [3].

А.С.Вирновский формуласы бойынша максималды жүктемені анықтамыз:

·

, (2.2.15)

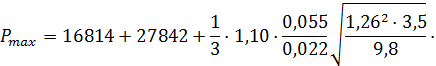
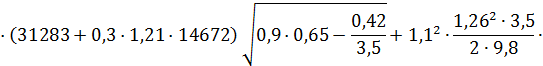
= +17225+3805=65686 H.

Минималды жүктеме:

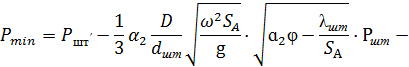
, (2.2.16)

=

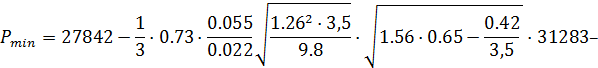
3. А.С.Вирновскийдің қарапайымдандырылған формулалары бойынша максималды және минималды жүктемелерді есептеймін:

, (2.2.17)

.

, (2.2.18)

P_min= -13391-1000=13451 H.

4. И.А.Чарный формуласы бойынша.

рад/с = , (2.2.19)

13,24°, tg13,24^o=0,235.

И.А.Чарный формуласы бойынша динамикалық теория негізіндегі максималды жүктемені былай анықтадым:

Р_max= P_c+P_ш[b+ · ], (2.2.20)

мұндағы tgµ/µ - штанга дірілін есепке алатын коэффициент.

P_max= +31283 [0,89+ · ]=53567 H.

Минималды жүктеме:

Р_min= P_ш[b - · ], (2.2.21)

P_min=31285(0,89-0,285)=18927 H.

5. А.И.Адонин формуласы бойынша

Кинематикалық коэффициент:

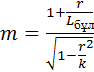, (2.2.22)

.

Сонда максималды жүктеме мәнін келесідей есептеймін:

, (2.2.23)

.

Сонымен, Вирновский формуласымен есептелген жүктемені негізгі деп алып, P_max бойынша оған жуық мәнді А.С.Вирновскийдің қарапайымдандырылған (-6639) және А.Н.Адонин (+13935) формулалары береді деуге болады; P_min-ге жақын мәнді қарапайымдандырылған А.С.Вирновский формуласы (+828 Н) көрсетеді.

Есепті шығаруға жұмсалынған еңбекті талдай отырып, бағалаушы және жуықтатылған есептер үшін И.М.Муравьевтің P_max-ға арналған формуласын және автормен айқындалған P_min мәні үшін қолдану керек, ал конструкторлық немесе дәлдік технологиялық есептер үшін А.С.Вирновский мен А.Н.Адониннің формулалары қолданады.