Тема 6. Методы выбора альтернатив управленческих решений в условиях неопределенности и риска

6.1 Принятие решений в условиях риска

Особенностью принятия решений в условиях риска состоит в том, что наступление определенных условий внешней среды ожидается с определенной вероятностью. Значения этой вероятности могут быть определены либо объективно на основании статистики или пробных испытаний, либо субъективно. Во всяком случае, эти вероятности известны.

Основой принятия решения в данных условиях является метод матрицы решений, описанный ранее. Следует напомнить, что в матрице отражаются объективные условия (неуправляемы факторы) через Y_j, варианты решений через R_j, а также ожидаемый результат при каждом сочетании объективных условий и вариантов решения - через Оij.

	Y1	Y2	Y3
R1	O11	O12	O13
R2	O21	O22	O23
R3	O31	O32	O33
R4	O41	O42	O43

Теорией и практикой принятия управленческих решений выработаны ряд правил, позволяющий осуществить выбор альтернативы в условиях риска.

Первое из них это правило модального значения (аксиома рациональности). В соответствии с ним учитываются только те результаты, вероятность появления которых максимальна. Это правило называют также аксиомой рациональности, поскольку при единичном выборе представляется разумным предполагать, что именно событие, имеющее максимальную вероятность появления, и наступит. Такой подход в большинстве случаев будет приводить к положительному результату. Однако он имеет и определенные недостатки. Например, он сталкивается с трудностями, когда:

-ряд состояний имеют равную вероятность появления;

-максимальный результат дают несколько альтернатив;

-вероятность появления модального значения при одном из состояний среды только незначительно выше, чем для других состояний среды, при этом другие альтернативы оказываются более оптимальными, иногда значительно¹.

Состояние среды	Р1	Р2	Р3	Р4	Р5	Р6	Р7	Р8	Р9	Р10
Вероятность появления	0,14	0,10	0,06	0,08	0,07	0,15	0,13	0,12	0,07	0,08
А1	5	4	4	5	1	6	8	6	10	3
А2	10	4	6	7	2	5	9	8	13	5
А3	11	3	7	7	1	3	7	7	12	4

Так, состояние среды Р₆ имеет наибольшую вероятность 0,15, и согласно правилу должна быть выбрана альтернатива А₁, дающая результат, равный 6. Однако состояние среды Р₁, имеющее незначительно меньшую вероятность появления 0,14, для альтернатив А₂ и А₃ дает заметно лучший результат. Поэтому целесообразность выбора альтернативы А₁ может вызывать сомнения.

Второе правило именуется правилом Байеса. Оно в отличие от предыдущего вовлекает в процесс выбора решения все имеющиеся значения. Для этого результат каждой альтернативы для каждого состояния среды умножается на вероятность ее появления.

Здесь р_кj- вероятность реализации к-го варианта ситуации.

Например, для альтернативы А₁ в указанной выше таблице сумма математических ожиданий будет равна 5,41 (j_А1=0,14*5+0,10*4+0,06*4+0,08*5+0,07*1+0,15*6+0,13*8+0,12*6+0,07*10+0,08*3= 5,41 ); j_А2 = 7,05; j_А3= 6,25. Оптимальный вариант в данном случае А₂, имеющий максимальное математическое ожидание.

Однако и правило Байеса при формальном применении может таить в себе опасность. В следующей таблице приведен пример, когда и по правилу модального значения (при Р₂ имеем максимальный результат), и в соответствии с правилом Байеса (сумма равна +6) выбор падает на альтернативу А₁.

Состояние среды	Р1	Р2	Сумма
Вероятность	0,4	0,6
А1	-600	+410	+6
А2	-10	+15	+5

При неоднократном выборе это решение было бы действительно оптимальным, но при однократном выборе альтернатива А₁ может оказаться убийственной, если реализуется значение среды Р₁. Следующего выбора, который позволил бы в конечном счете выиграть, может просто не быть из-за банкротства в результате первого выбора.

Поэтому для исключения подобного варианта применяется критерий среднего значения и стандартного отклонения. Для оценки рассеяния значений критерия (выбранного параметра) относительно его среднего прогнозируемого значения математического ожидания целесообразно использовать такую характеристику, стандартное отклонений (среднеквадратичное отклонение). Критерий применяется для учета отношения к риску. Для этого помимо математического ожидания рассчитывают стандартное отклонение результатов. Чем выше стандартное отклонение, тем больше риск. Полезность альтернативных решений (риска) зависит от математического ожидания и стандартного отклонения. Эта зависимость может быть отражена функцией приоритетности риска, которая характеризует отношение лица, принимающего решение, к риску. При боязни риска лицо, принимающее решение, выбирает из двух альтернатив с одинаковыми математическими ожиданиями ту, которая имеет наименьшее стандартное отклонение.

Стандартное отклонение высчитывается по формуле:

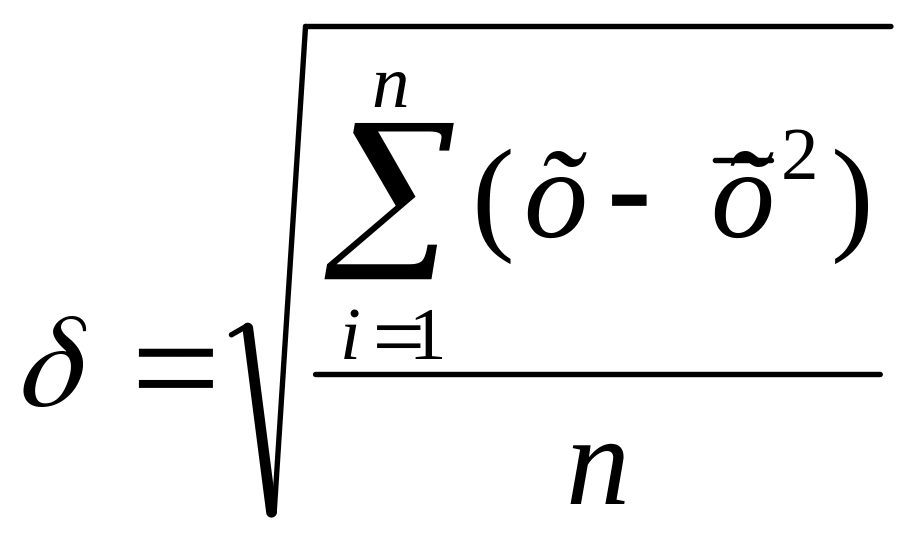, где

x – ожидаемый результат;

– среднее значение показателя;

n – количество значений в анализируемой совокупности данных.

Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n-1:

.

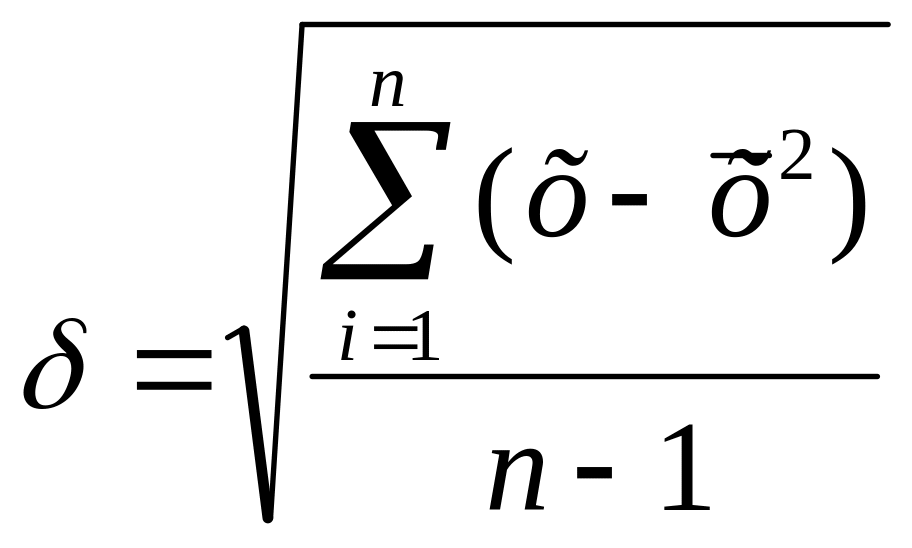В приведенном примере стандартные отклонения А₁ и А₂:

Состояние среды	Р1	Р2	Сумма	δ
Вероятность	0,4	0,6
А1	-600	+410	+6	714,18
А2	-10	+15	+5	17,68

Третье правило - правило Бернулли достаточно широко используется для принятия экономических решений в условиях риска. Оно отличается от правила Байеса тем, что вводится индивидуальная функция полезности. При этом каждое значение в таблице вначале умножается на соответствующее значение функции полезности и уж затем на вероятность соответствующего состояния среды. Далее для каждой альтернативы производится суммирование по всем состояниям среды. Максимальная сумма определяет лучшую альтернативу.

Преимущество этого подхода заключается в учете индивидуальных предпочтений лица принимающего решения. Недостаток правила связан с тем, что функция полезности должна быть определена настолько точно, чтобы быть справедливой для лица принимающего решения и в других ситуациях, и должна быть стабильна во времени, т.е. должна быть применима для конкретных ситуаций и в другое время.

Сущность правила Бернулли можно показать на простейшем бытовом примере. Уходя на работу вы задумываетесь: брать с собой зонт или нет. Возможность дождя от вас не зависит - это объективные условия внешней среды. Возможны два варианта решений: взять зонт (а₁) и не брать зонт (а₂). На ваш выбор повлияют внешние условия: пойдет дождь (у₁) или не пойдет (у₂). Допустим, вы считаете, что вероятность дождя Ру₁ = 0,5, тогда вероятность хорошей погоды 1- 0,5 = 0,5 (Ру₂ =1- Ру₁).

Далее необходимо дать оценку потерь (неудобств), которые можно иметь по вариантам возможных решений и влияния погодных условий. Это оценка у разных людей может быть различной (в данном случае в зависимости от отношения индивидуума к дождю и сохранению своей одежды). Но у большинства людей существует какое-то среднее мнение. При решении сложных проблем на данном этапе может быть использован метод экспертных оценок возможных потерь.

В нашем случае примем следующую оценку. По варианту а₁ (взять зонт) оценка будет равна 1 (а₁₁), если дождь пойдет, и 2 (а₁₂), если дождя не будет. Это означает, что во время кратковременного пребывания на улице дождя не будет и неудобство носить зонт оценивается единицей, а если вообще дождь не пойдет, то неудобство увеличится вдвое.

По варианту а₂ соответственно возможны два события:

дождь пойдет а₂₁ - оценивается числом 6 (опасность испортить одежду, прическу во время дождя при отсутствии зонта) и а₂₂ = 0 - при отсутствии зонта и дождя.

Составим таблицу потерь на основе рассуждений и принятых оценок:

Линия поведения	Объективные условия
	дождь (у1)	нет дождя (у2)
взять зонт (а1)	1 (а11)	2 (а12)
не брать зонт (а2)	6 (а21)	0 (а22)

Далее определим математическое ожидание потерь при выборе альтернативных линий поведения. Так как математическое ожидание (Е) случайной величины равно E_x = ΣP_jX_j, то в нашем случае, при вероятности Р= 0,5, для а₁ и а₂ оно будет равно соответственно:

Ea₁ = 0,5 *1+0,5*2= 1,5

Еа₂= 0,5*6+0,5*0=3,0

Чтобы минимизировать возможные потери, в нашем примере необходимо остановить выбор на линии поведения а₁, то есть взять зонт¹.