4.3 Методы экстраполяции

При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта, т.е. прогноз осуществляется на основе поведения объекта в прошлом. Экстраполируются оценочные функциональные системные и структурные характеристики. Экстраполяционные методы являются одними из самых распространенных и наиболее разработанных среди всей совокупности методов прогнозирования.

С помощью этих методов экстраполируются количественные параметры больших систем, количественные социально-экономические характеристики различный явлений и др.

Однако степень реальности такого рода прогнозов и соответственно мера доверия к ним в значительной мере обусловливаются аргументированностью выбора пределов экстраполяции и стабильностью соответствия "измерителей" по отношению к сущности рассматриваемого явления. Следует обратить внимание на то, что сложные объекты, как правило, не могут быть охарактеризованы одним параметром. В связи с этим можно сделать некоторое представление о последовательности действий при статистическом анализе тенденций и экстраполировании, которое состоит в следующем:

- во-первых, должно быть четкое определение задачи, выдвижение гипотез о возможном развитии прогнозируемого объекта, обсуждение факторов, стимулирующих и препятствующих развитию данного объекта, определение необходимой экстраполяции и её допустимой дальности;

- во-вторых, выбор системы параметров, унификация различных единиц измерения, относящихся к каждому параметру в отдельности;

- в-третьих, сбор и систематизация данных. Перед сведением их в соответствующие таблицы еще раз проверяется однородность данных и их сопоставимость;

- в-четвертых, когда вышеперечисленные требования выполнены, задача состоит в том, чтобы в ходе статистического анализа и непосредственной экстраполяции данных выявить тенденции или симптомы изменения изучаемых величин. В экстраполяционных прогнозах особо важным является не столько предсказание конкретных значений изучаемого объекта или параметра в таком-то году, сколько своевременное фиксирование объективно намечающихся сдвигов, лежащих в зародыше назревающих тенденций.

Для повышения точности экстраполяции используются различные приемы. Один из них состоит, например, в том, чтобы экстраполируемую часть общей кривой развития (тренда) корректировать с учетом реального опыта развития отрасли-аналога исследований или объекта, опережающих в своем развитии прогнозируемый объект¹.

Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20-25 лет. Применяемый в прогнозировании метод экстраполяции не дает точных результатов на длительный срок прогноза, потому что данный метод исходит из прошлого и настоящего, и тем самым погрешность накапливается. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов не более 5 лет.

Наиболее распространенными являются методы экстраполяции по математическим моделям и графический (от руки, на глазок). Оба метода требуют наличия информации о прогнозируемом параметре объекта за период в 2 и более раза больше прогнозируемого периода. Для учета изменений качества объекта в прогнозируемом периоде и организационно-технического уровня производства у изготовителя и потребителя объекта применяются корректирующие коэффициенты¹.

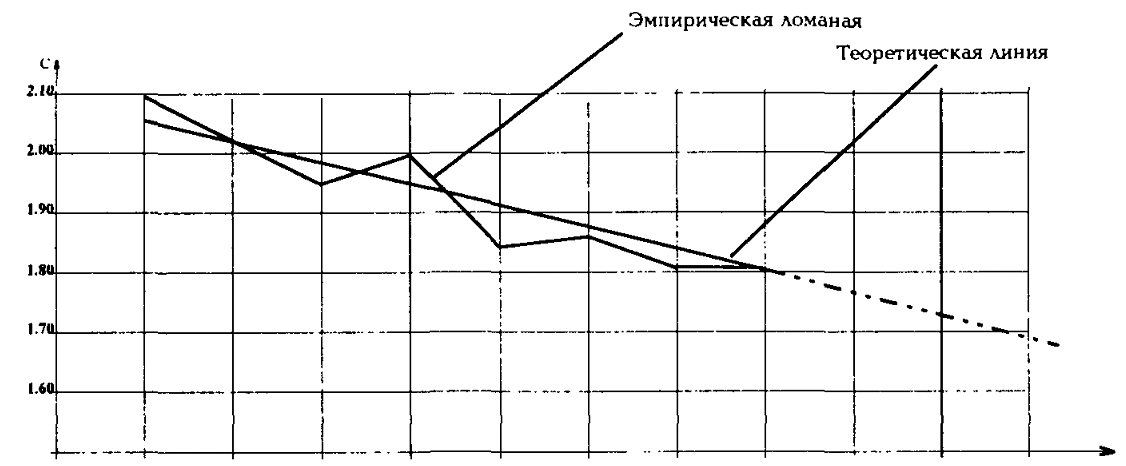
К математическим методам прогнозной экстраполяции относят:

метод проецирования трендов (аналитического выравнивания динамических рядов по прямой);

метод выравнивания по среднегодовому коэффициенту роста;

метод скользящих средних;

метод экспоненциального сглаживания и другие.

Метод проецирования трендов (аналитического выравнивания динамических рядов по прямой). Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание относительно плавной линии развития ряда.

Простейшей математической формулой, выражающей тенденции развития, является формула прямой линии. Прямая линия характеризует равномерное изменение динамики. Выравнивание по прямой осуществляется методом наименьших квадратов. Этот метод обеспечивает минимальную разность между фактическими и теоретическими уровнями.

Выравнивание, как особый способ обработки динамических рядов, решает задачу выявления тенденций развития того или иного явления к настоящему моменту. Однако не с меньшим успехом он может использоваться и при определении тенденций развития явлений в будущем.

Итак, имея динамический ряд (t_п) количества зарегистрированных преступлений, можно рассчитать прогноз возможного количества преступлений на следующий (t_п +1) год, используя уравнение прямой:

Параметры уравнения а и b определяются методом «наименьших квадратов» по формулам:

; ,

где

y – динамический ряд показателей,

t - порядковый номер года в ряду динамики,

n - число лет базисного периода,

- средние значения данных показателей,

Σ - знак сложения указанных величин.

В качестве примера расчета данным методом прогнозирования можно взять динамику уровня преступности в России (на 100 000 человек).

Годы	Зарегистрировано преступлений на 100 000 человек	Порядковый номер года в ряду динамики	(yt)	(t2)
	(у)	(t)
2003	1906	1	1906	1
2004	2009	2	4018	4
2005	2477	3	7431	9
2006	2695	4	10780	16
2007	2509	5	12545	25
2008	2249	6	13494	36
2009	2097	7	14679	49
2010	1840	8	14720	64
2011	1682	9	15138	81
2012	1608	10	16080	100
Σ	21072	55	110791,00	385

На основе приведенных данных порядок расчета параметров а и b следующий:

y = 21072:10=2107,2

t = 55:10=5,5

Подставив полученные данные в формулы указанные выше будем иметь:

Таким образом, уравнение, характеризующее уровень преступности в 2013 году, имеет вид

Для прогноза возможного уровня преступности в следующем году (текущем, плановом) подставляем порядковые номера ряда динамики, соответствующие этим годам. Так, для 2013 года t будет равно 11 (как было рассчитано), для 2014 года - 12. Тогда возможный уровень преступности в 2013 году соответственно будет равен:

.

Следует подчеркнуть, что метод проецирования тренда применяется тогда, когда динамика показателей близка к прямой. В противном случае его точность будет не удовлетворительной.

Оценить среднюю относительную ошибку данного метода можно по формуле:

, где

- фактическое количество зарегистрированных преступлений на 100 000 человек;

- рассчитанное (теоретическое) количество преступлений на 100 000 человек.

Чтобы воспользоваться этой формулой надо построить таблицу, в которую вносятся рассчитанные и фактические показатели.

Годы	Фактическое количество зарегистрированных преступлений на 100 000 человек .	Порядковый номер года в ряду динамики (t)	Рассчитанное количество преступлений на 100 000 человек .	Относительная ошибка ε,%
2003	1906	1	=2447,65-61,9*1=2385,75	25,17
2004	2009	2	=2447,65-61,9*2=2323,85	15,67
2005	2477	3	=2447,65-61,9*3=2261,95	8,68
2006	2695	4	=2447,65-61,9*4=2200,05	18,37
2007	2509	5	=2447,65-61,9*5=2138,15	14,78
2008	2249	6	=2447,65-61,9*6=2076,25	7,68
2009	2097	7	=2447,65-61,9*7=2014,35	3,94
2010	1840	8	=2447,65-61,9*8=1952,45	6,11
2011	1682	9	=2447,65-61,9*9 =1890,55	12,40
2012	1608	10	=2447,65-61,9*10=1828,65	13,72
Итого				126,53

Произведя соответствующие вычисления, можно получить среднюю относительную ошибку:

%. Точность прогноза хорошая.

Касаемо последнего надо отметить следующее.

Точность прогноза считается:

1. высокой, если средняя относительная ошибка (ε) менее 10 %;

2. хорошей – 10-20 %;

3. удовлетворительной – 20-50%;

4. неудовлетворительной – более 50%.

Метод выравнивания по среднегодовому коэффициенту роста. Если значения уровней динамического ряда последовательно увеличиваются или последовательно уменьшаются, то экстраполяцию можно осуществлять посредством нахождения среднего темпа роста, а он определяется с помощью среднего геометрического. Умножая последний известный уровень ряда на средний темп, находим первый расчетный уровень; умножая его на средний темп роста, находим второй расчетный уровень и т.д.

Среднегодовой коэффициент роста (снижения) определяется по формуле:

где k - среднегодовой коэффициент роста (снижения)

n - число лет базисного периода

y_n - конечный уровень базисного динамического ряда

y₀ - начальный уровень базисного динамического ряда.

При прогнозировании уровней преступности каждый последующий уровень принимается равным предыдущему, умноженному на средний коэффициент роста (снижения).

Пример расчета прогноза уровня преступности

n=10 лет

y₂₀₁₂ = 1608

y₂₀₀₃= 1906

Среднегодовой коэффициент роста (k) будет равен:

k = 0,98

Прогноз возможного уровня преступности составит:

y₂₀₁₃ = k*y₂₀₁₂ ; y₂₀₁₄ = k*y₂₀₁₃=k*k* y₂₀₁₂

y₂₀₁₂ = 0,98*1608 = 1577,91; y₂₀₁₃ =0,98*1577,91= 1548,38.

Точность данного метода оценивается по тому же алгоритму и схожей формуле, что и в ходе применения метода проецирования тренда.

Годы	Фактическое количество зарегистрированных преступлений на 100 000 человек .	Порядковый номер года в ряду динамики (t)	Рассчитанное количество преступлений на 100 000 человек .	Относительная ошибка ε,%
2003	1906	1
2004	2009	2	=0,98*1906=1867,88	7,02
2005	2477	3	=0,982*1906=1830,52	26,10
2006	2695	4	=0,983*1906=1793,91	33,44
2007	2509	5	=0,984*1906=1758,03	29,93
2008	2249	6	=0,985*1906=1722,87	23,39
2009	2097	7	=0,986*1906=1688,42	19,48
2010	1840	8	=0,987*1906=1654,65	10,07
2011	1682	9	=0,988*1906=1621,55	3,59
2012	1608	10	=0,989*1906=1589,12	1,17
Итого				154,21

. Точность прогноза хорошая.

Следующим метод экстраполяционного прогнозирования – это метод скользящих средних, который является одним из широко известных методов сглаживания временных рядов. Применяя этот метод, можно элиминировать случайные колебания и получить значения, соответствующие влиянию главных факторов.

Сглаживание с помощью скользящих средних основано на том, что в средних величинах взаимно погашаются случайные отклонения. Это происходит вследствие замены первоначальных уровней временного ряда средней арифметической величиной внутри выбранного интервала времени. Полученное значение относится к середине выбранного интервала времени (периода).

Затем период сдвигается на одно наблюдение, и расчет средней повторяется. При этом периоды определения средней берутся все время одинаковыми. Таким образом, в каждом рассматриваемом случае средняя центрирована, т.е. отнесена к серединной точке интервала сглаживания и представляет собой уровень для этой точки.

При сглаживании временного ряда скользящими средними в расчетах участвуют все уровни ряда. Чем шире интервал сглаживания, тем более плавным получается тренд. Сглаженный ряд короче первоначального на (n–1) наблюдений, где n – величина интервала сглаживания.

При больших значениях n колебания сглаженного ряда значительно снижается. Одновременно заметно сокращается количество наблюдений, что создает трудности.

Выбор интервала сглаживания зависит от целей исследования. При этом следует руководствоваться тем, в какой период времени происходит действие, а следовательно, и устранение влияния случайных факторов.

Данный метод используется при краткосрочном прогнозировании. Его рабочая формула:

если n=3,

где

t+1 – прогнозный период;

t – период, предшествующий прогнозному периоду (год, месяц и т.д.);

y_t+1 – прогнозируемый показатель;

m_t-1 – скользящая средняя за два периода до прогнозного;

n – число уровней, входящих в интервал сглаживания;

y_t – фактическое значение исследуемого явления за предшествующий период;

y_t-1 – фактическое значение исследуемого явления за два периода, предшествующих прогнозному.

Рассчитать скользящую среднею при n=3 можно по формуле:

.

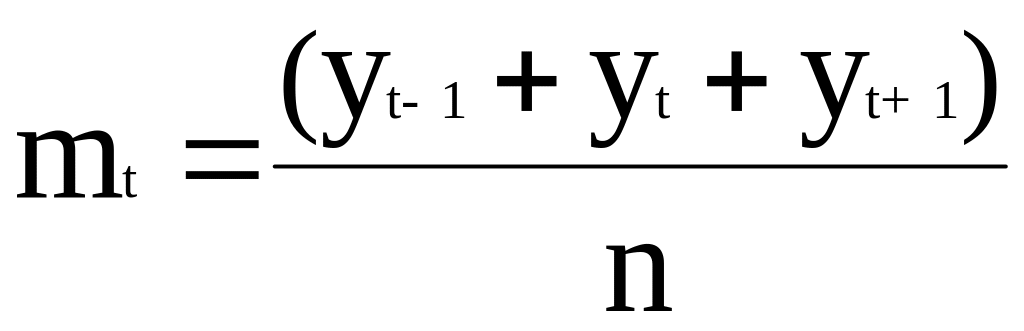При иных значениях n формулы будут выглядеть следующим образом

,

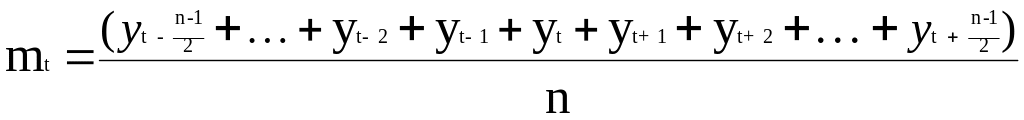
Здесь следует еще раз отметить, что t является центром интервала n, а сам интервал n для удобства берется нечетным.

Метод скользящих средних прост и удобен, но его не следует использовать для среднесрочных и долгосрочных прогнозов. По той причине, что в ходе прогнозирования при небольших интервалах на длительные сроки получаемые значения вырождаются в параллельную оси Х прямую. Общие тенденции к снижению и повышению тренда им не улавливаются.

При расчете прогноза состояния преступности данным методом для удобства следует построить таблицу.

Годы	Фактическое количество зарегистрированных преступлений на 100 000 человек .	Скользящее среднее	Относительная ошибка ε,%
2003	1906
2004	2009	2130,67
2005	2477	2393,67	3,36
2006	2695	2560,33	5,00
2007	2509	2484,33	0,98
2008	2249	2285,00	1,60
2009	2097	2062,00	1,67
2010	1840	1873,00	1,79
2011	1682	1710,00	1,66
2012	1608
Итого			22,13

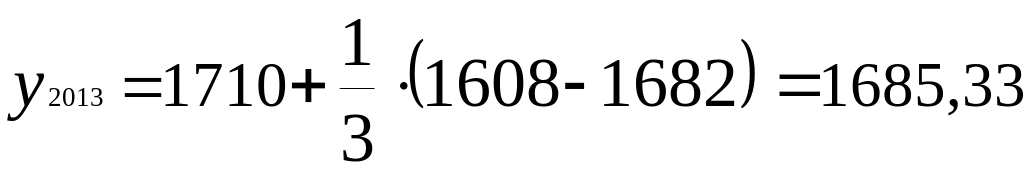
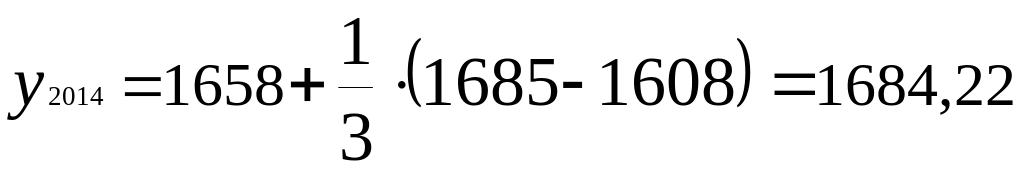
Точность прогноза рассчитывается по уже знакомой формуле.

%. Точность прогноза высокая.

Метод экспоненциального сглаживания наиболее эффективен при разработке среднесрочных прогнозов. Он приемлем при прогнозировании только на один период вперед. Его основные достоинства простота процедуры вычислений и возможность учета весов исходной информации. Рабочая формула метода экспоненциального сглаживания:

где t – период, предшествующий прогнозному;

t+1 – прогнозный период;

U_t+1 - прогнозируемый показатель;

α - параметр сглаживания;

y_t - фактическое значение исследуемого показателя за период, предшествующий прогнозному;

U_t - экспоненциально взвешенная средняя для периода, предшествующего прогнозному.

При прогнозировании данным методом возникает два затруднения:

• выбор значения параметра сглаживания α;

• определение начального значения U₀.

От величины α зависит, как быстро снижается вес влияния предшествующих наблюдений. Чем больше α, тем меньше сказывается влияние предшествующих лет. Если значение α близко к единице, то это приводит к учету при прогнозе в основном влияния лишь последних наблюдений. Если значение α близко к нулю, то веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения.

Таким образом, если есть уверенность, что начальные условия, на основании которых разрабатывается прогноз, достоверны, следует использовать небольшую величину параметра сглаживания (α→0). Когда параметр сглаживания мал, то исследуемая функция ведет себя как средняя из большого числа прошлых уровней. Если нет достаточной уверенности в начальных условиях прогнозирования, то следует использовать большую величину α, что приведет к учету при прогнозе в основном влияния последних наблюдений.

Точного метода для выбора оптимальной величины параметра сглаживания α нет. В отдельных случаях автор данного метода профессор Браун предлагал определять величину α, исходя из длины интервала сглаживания. При этом α вычисляется по формуле:

где n – число наблюдений, входящих в интервал сглаживания.

Задача выбора U₀ (экспоненциально взвешенного среднего начального) решается следующими способами:

• если есть данные о развитии явления в прошлом, то можно воспользоваться средней арифметической и приравнять к ней U₀;

• если таких сведений нет, то в качестве U₀ используют исходное первое значение базы прогноза y₁.

Также можно воспользоваться экспертными оценками.

Следует отметить, что в случае изучения небольших временных рядов (15-20 наблюдений) при высоких темпов роста метод экспоненциального сглаживания не в состоянии отразить все изменения.

Это обусловлено тем, что экономические временные ряды бывают слишком короткими (15-20 наблюдений), и в случае, когда темпы роста и прироста велики, данный метод не «успевает» отразить все изменения¹.

В качестве иллюстрации будет использован тот же пример с преступностью.

Прежде всего необходимо определить α, которое высчитывается по упомянутой выше формуле:

Далее следует определить U₀ двумя способами.

1 способ при U₀ = средней арифметической, т.е.

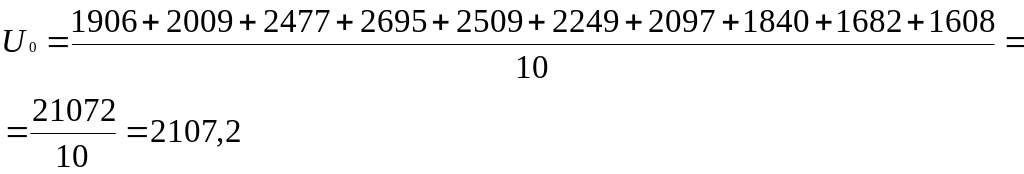
; и т.д.

;

;

2 способ при U₀= y₁,

и т.д.

Годы	Фактическое количество зарегистрированных преступлений на 100 000 человек .	Экспоненциально взвешенная среднее,		Относительная ошибка ε,%
		1 способ	2 способ	1 способ	2 способ
2003	1906	2107,2	1906	10,56	0
2004	2009	2070,98	1906,00	3,09	5,13
2005	2477	2059,83	1924,54	16,84	22,30
2006	2695	2134,92	2023,98	20,78	24,90
2007	2509	2235,73	2144,77	10,89	14,52
2008	2249	2284,92	2210,33	1,60	1,72
2009	2097	2278,46	2217,29	8,65	5,74
2010	1840	2245,79	2195,64	22,05	19,33
2011	1682	2172,75	2131,62	29,18	26,73
2012	1608	2084,42	2050,69	29,63	27,53
Итого				153,27	147,89

Относительная ошибка прогноза при первом способе %, а при втором %. Точность прогноза хорошая.

Если изобразить вычисления на графике, то можно увидеть нижеследующее.

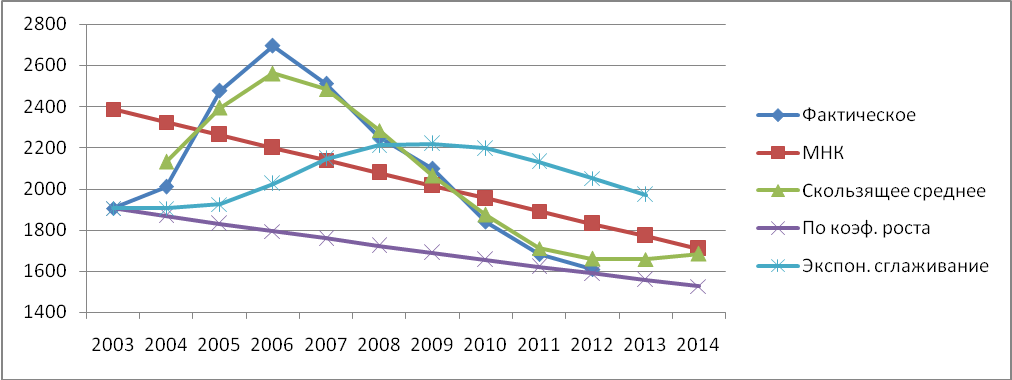
Нельзя сказать, что какой-то из описанных методов является самым точным при любых условиях. Выбор метода зависит от конкретной ситуации и вида прогнозирования. При краткосрочном прогнозировании в условиях быстрого изменения соответствующего показателя целесообразно рассчитать скользящее среднее. В условиях плавного повышения (снижения) – среднегодовой коэффициент роста (снижения). Метод проецирования тренда лучше применить тогда, когда разброс численных данных концентрируется возле прямой. Экспоненциальное сглаживание приемлемо в ходе среднесрочного прогнозирования, если отсутствуют резкие скачки кривой.