Ответы к заданиям варианта в – 2014 – 11

№ задания	ответ
В1	9
В2	570
В3	1
В4	219750
В5	9
В6	0,92
В7	84,5
В8	22
В9	8
В10	96
В11	- 1,5
В12	6
В13	6,75
В14	72
В15	3

Новые задания егэ

З а д а н и я В1

1. В доме, в котором живет Маша, 9 этажей и несколько подъездов. На каждом этаже находится по 4 квартиры. Маша живет в квартире № 130 . В каком подъезде живет Маша?

2. В розницу один номер еженедельного журнала стоит 24 рубля, а полугодовая подписка на этот журнал стоит 460 рублей. За полгода выходит 25 номеров журнала. Сколько рублей можно сэкономить за полгода, если не покупать каждый номер журнала отдельно, а получать журнал по подписке?

3. Установка двух счётчиков воды (холодной и горячей) стоит 3300 рублей. До установки счётчиков Александр платил за воду (холодную и горячую) ежемесячно 800 рублей. После установки счётчиков оказалось, что в среднем за месяц он расходует воды на 300 рублей при тех же тарифах на воду. За какое наименьшее количество месяцев при тех же тарифах на воду установка счётчиков окупится?

З а д а н и я В2

1. Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.

2. Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 37000 футов. Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.

3. Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

З а д а н и я В4

1. Керамическая плитка одной и той же торговой марки выпускается трёх разных размеров. Плитки упакованы в пачки. Пользуясь данными таблицы, определите, в каком случае цена одного квадратного метра плитки будет наименьшей.

Размер плитки  (см на см)	Количество плиток в пачке	Цена пачки
20 на 20	25	604 р.
20 на 30	16	595 р. 20 к.
30 на 30	11	594 р.

В ответ запишите найденную наименьшую цену квадратного метра в рублях.

2. В трёх салонах сотовой связи один и тот же телефон продаётся в кредит на разных условиях. Условия даны в таблице.

Салон	Цена телефона (руб.)	Первоначальный взнос (в % от цены)	Срок кредита (мес.)	Сумма ежемесячного платежа (руб.)
Эпсилон	20000	15	12	1620
Дельта	21000	10	6	3400
Омикрон	19000	20	12	1560

Определите, в каком из салонов покупка обойдётся дешевле всего (с учётом переплаты).

В ответ запишите эту сумму в рублях.

3. Рейтинговое агентство определяет рейтинг соотношения «цена-качество» электрических фенов для волос. Рейтинг вычисляется на основе средней цены P и оценок функциональности F , качества Q и дизайна D . Каждый отдельный показатель оценивается экспертами по пятибалльной шкале целыми числами от 0 до 4 . Итоговый рейтинг вычисляется по формуле

R = 3(F + Q) + D – 0,01 P . В таблице даны оценки каждого показателя для нескольких моделей фенов. Определите, какая модель имеет наименьший рейтинг. В ответ запишите значение этого рейтинга.

Модель фена	Средняя цена	Функциональность	Качество	Дизайн
А	1200	1	3	1
Б	3200	2	3	4
В	5500	3	0	0
Г	5700	3	2	3

З а д а н и я В5

1. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32 ?

2. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна  1 . Найдите площадь заштрихованной фигуры.

З а д а н и я В6

1. В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.

2. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10 , но не дойдя до отметки 1 час.

3. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

4. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

5. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

6. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.

7. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

З а д а н и я В12

1. Рейтинг R интернет-магазина вычисляется по формуле 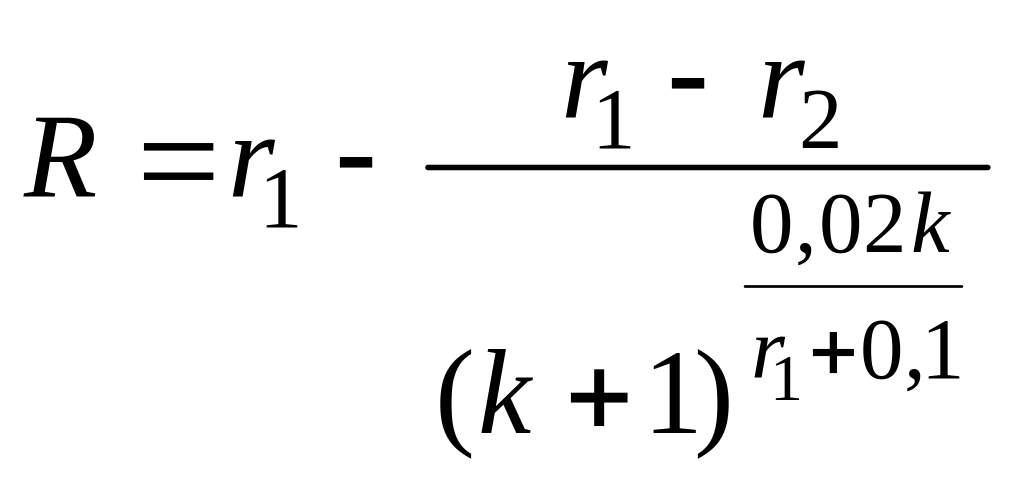, где r₁ – средняя оценка магазина покупателями ( от 0 до 1 ) , r₂ – оценка магазина экспертами (от 0 до 0,7 ) и k  – число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оставивших отзыв о магазине, равно 24 , их средняя оценка равна 0,86 , а оценка экспертов равна 0,11 .

2. Катер должен пересечь реку шириной L = 100 м и со скоростью течения u = 0,5 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением , где  – острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом (в градусах) нужно плыть, чтобы время в пути было не больше 200 секунд?

3. Небольшой мячик бросают под острым углом к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой , где = 20 м/с  – начальная скорость мячика, а g – ускорение свободного падения (считайте g = 10 м/с²). При каком наименьшем значении угла (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м ?

4. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле , где m = 1200 кг  – общая масса навеса и колонны, D  – диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с² , а , определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па . Ответ выразите в метрах.

5. При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где  = 5 м  – длина покоящейся ракеты,  км/с – скорость света, а v  – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м ? Ответ выразите в км/с .

З а д а н и я В13

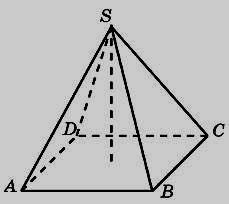
1. В правильной четырехугольной пирамиде высота равна 12 , объем равен 200 . Найдите боковое ребро этой пирамиды.

2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ ребро AB = 2 , ребро AD = , ребро AA₁ = 2 . Точка K – середина ребра BB₁ . Найдите площадь сечения, проходящего через точки A₁ , D₁ и K .

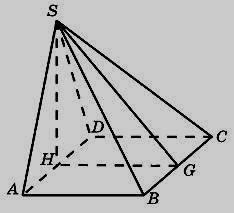
3. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен  , а высота равна 2 .

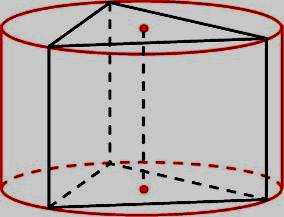
4. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60⁰ . Высота пирамиды равна 6 . Найдите объем пирамиды.

5. Диагональ прямоугольного параллелепипеда равна и образует углы 30⁰ , 30⁰ и 45⁰ с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

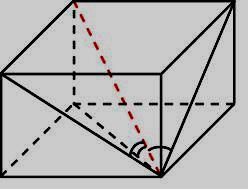
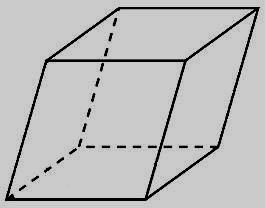
6. Гранью параллелепипеда является ромб со стороной 1 и острым углом 30⁰ . Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 30⁰ и равно 2 . Найдите объем параллелепипеда.

З а д а н и я В14

1. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут?

2. Клиент А. сделал вклад в банке в размере 7700  рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Еще ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 847  рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?

З а д а н и я В15

1. Найдите наибольшее значение функции на отрезке .

2. Найдите наименьшее значение функции на отрезке .

3. Найдите наибольшее значение функции .

О т в е т ы :

З а д а н и я В 1	1	2	3
	4	140	7

З а д а н и я В 2	1	2	3
	36	11285	163

З а д а н и я В 4	1	2	3
	600	22440	-46

З а д а н и я В 5	1	2
	96	3

З а д а н и я В 6	1	2	3	4	5	6	7
	0,498	0,25	0,20	0,8836	0,42	0,0296	0,0545

З а д а н и я В 12	1	2	3	4	5
	0,71	45	30	0,2	180000

З а д а н и я В 13	1	2	3	4	5	6
	13	5	36	48	4	0,5

З а д а н и я В 14	1	2
	108	10

З а д а н и я В 15	1	2	3
	48	-6	4