Регрессионный анализ статистических данных

Задачи регрессионного анализа:

• построение математической модели регрессии в виде зависимости среднего значения результативного признака от факторных признаков;

• оценка параметров модели регрессии и установление ее соответствия выборочным наблюдениям (оценка качества модели регрессии);

• определение точечных и интервальных прогнозов результативного признака.

Парный линейный регрессионный анализ

Уравнение регрессии выглядит следующим образом:

где - оценки параметров функции регрессии (параметры уравнения регрессии) или параметры модели регрессии.

Параметры модели регрессии должны быть подобраны таким образом, чтобы линия регрессии, построенная по уравнению , располагалась как можно ближе ко всем точкам корреляционного поля, т.е. проходила практически через его центр. Удобно определять значения параметров и оценивать качество модели регрессии с помощью инструмента Регрессия пакета анализа

Выходная информация представлена в следующей таблице:

В ячейках таблицы 11 приведена следующая информация:

• ячейка В4 – множественный коэффициент корреляции (в данном случае это коэффициент парной корреляции r₁₂y₂;

• ячейка В5 – коэффициент детерминации

• ячейка В5 – нормированный коэффициент детерминации, определяемый по формуле

где - объем выборки, - число неизвестных параметров уравнения регрессии. Коэффициент детерминации корректируется с учетом числа факторных признаков и объема выборки.

• ячейка В7 – стандартная ошибка ;

• ячейка В8 – объем выборки ;

• ячейка В12 – число степеней свободы 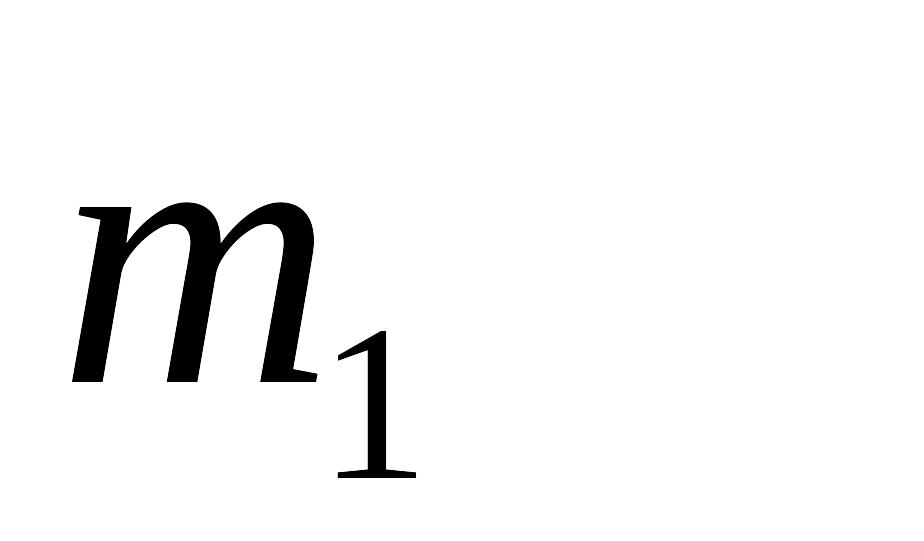для определения критического значения критерия Фишера;

• ячейка В13 – число степеней свободы для определения критического значения критерия Фишера;

• ячейка С12 – сумма квадратов разностей между расчетными значениями и средним значением результативного признака т.е. сумма квадратов, объясняемая регрессией ( );

• ячейка С13 – остаточная сумма квадратов, т.е. сумма квадратов отклонений ;

• ячейка D13 – остаточная дисперсия

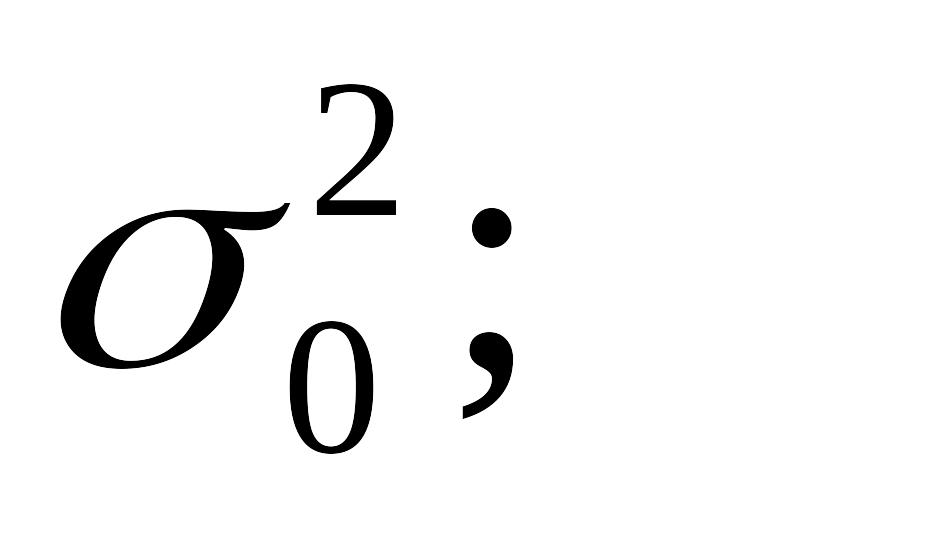
• ячейка Е12 – расчетное значение критерия Фишера;

• ячейка В17 – параметр уравнения регрессии;

• ячейка В18 - параметр уравнения регрессии;

• ячейка С17 – стандартная ошибка параметра ;

• ячейка С18 - стандартная ошибка параметра ;

• ячейка D17 – расчетное значение 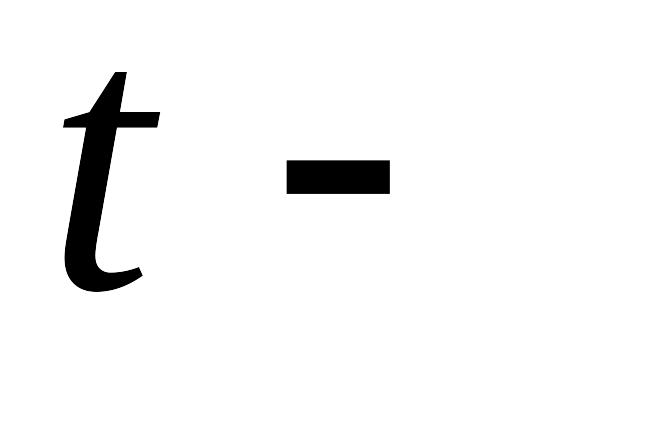статистики параметра ;

• ячейка D18 - расчетное значение статистики параметра ;

• ячейка Е17 - значение параметра ;

• ячейка Е18 - значение параметра ;

• ячейки F17:F18 – нижние границы доверительных интервалов соответствующих параметров уравнения регрессии;

• ячейки G17:G18 – верхние границы доверительных интервалов этих параметров.

Для оценки статистической значимости параметров модели регрессии удобно использовать метод значение ( value). Обозначив через уровень значимости, получают следующее правило принятия решения:

• принять нулевую гипотезу о том, что параметр модели регрессии может быть равен нулю, если

• отвергнуть нулевую гипотезу, если