Министерство образования и науки Украины

Приднепровская государственная академия

строительства и архитектуры

Кафедра прикладной математики

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

ДАННЫХ НАБЛЮДЕНИЙ

Вариант №14

Выполнила:студ. гр. ЭП-12 . Кравчук Н.Н.

Руководитель:ст.преп.

Кривенкова Л.Ю.

Днепропетровск – 2014 г. Задание

Выполнить корреляционно-регрессионный анализ следующих показателей производственно-хозяйственной деятельности предприятий машиностроения:

- индекс снижения себестоимости продукции;

- трудоемкость единицы продукции;

- фондовооруженность труда, грн.;

- среднегодовая численность ППП, чел.;

Определить прогнозируемые значения индекса снижения себестоимости на основе уравнений регрессии и методов оптимизации.

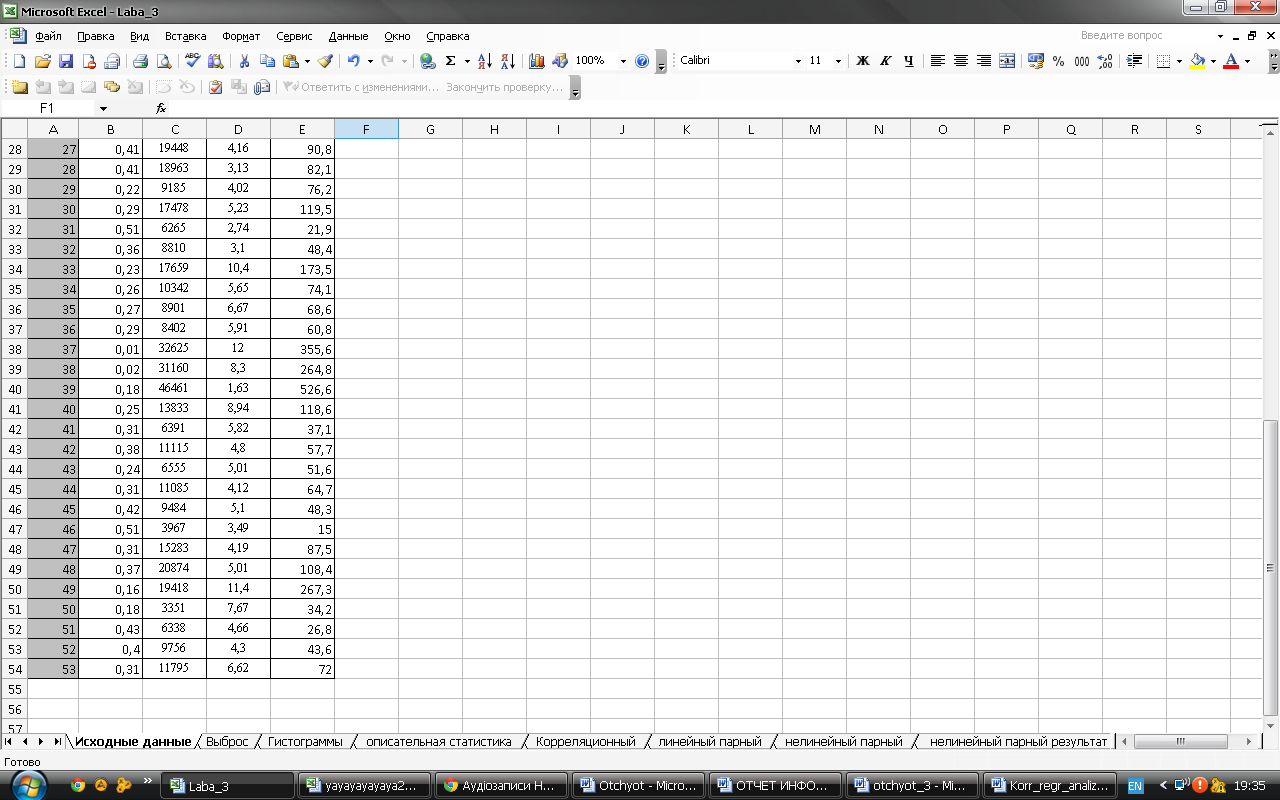
Рис 1. Размещение исходной информации на рабочем листе.

Краткие сведения из теории и компьютерной технологии

Суть корреляционно-регрессионного метода состоит в том, что на основе имеющейся информации, полученной в результате статистических наблюдений за прошлое время, составляются уравнения регрессии, представляющие собой математические модели. Они могут быть линейными и нелинейными. По математическим моделям регрессии можно прогнозировать, т.е. находить прогнозные значения результативного признака при увеличении (уменьшении) значений входящих в модель регрессии факторных признаков на 10-15%.

Уравнения регрессии в отличие от функциональных уравнений устанавливают зависимости между случайными переменными.

Во время статистических наблюдений для каждого объекта часто можно измерить (получить) значения нескольких признаков. В итоге получается многомерная выборка.

Смысл обработки многомерных выборок заключается в установлении связи между признаками. Для этого их делят на факторные и результативные. Факторный признак вызывает изменение других, связанных с ним, признаков. Результативный признак изменяется под действием факторных признаков.

Связь может быть функциональной, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Если зависимость проявляется не в каждом отдельном случае, а в среднем при большом числе наблюдений, то она называется статистической (стохастической). В этом случае в расчетах используют среднее значение признака. Частным случаем статистической связи является корреляционная связь, при которой исследуется зависимость среднего значения результативного признака от факторных признаков.

Контроль исходной информации на наличие грубых ошибок и выбросов

Для проверки исходной информации на наличие выбросов используют в зависимости от объема выборки критерий:

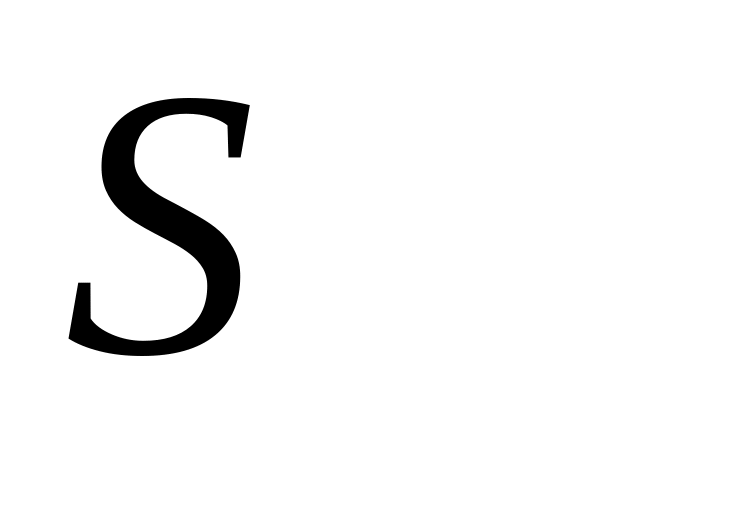• - критерий для выборки, содержащей более 25 элементов;

По заданию объем выборки , следовательно, экстремальные значения должны быть проверены по критерию . Расчетное значение критерия определяется по формуле:

(1)

где - выборочное среднее и - стандартное отклонение, для признака, в котором обнаружено экстремальное значение; - экстремальное значение (предполагаемый выброс). Критическое значение критерия берется по таблице 1.

Т а б л и ц а 1

Критические значения критерия

Объем выборки	Уровень значимости
	=0,05	=0,01
30	2,929	3,402
50	3,082	3,539
100	3,283	3,718
1000	3,884	4,264

Если то экстремальное значение с вероятностью не является выбросом, т.е. его нельзя исключать из выборки. В этом случае экстремальное значение объясняется проявлением изменчивости, характерной для данной генеральной совокупности.

При из многомерной выборки исключается строка с экстремальным значением.

Выстраиваем значения признака в порядке уменьшения. В среде ЭТ с помощью мастера функций определяем для массива У₂ выборочное среднее(x̅), стандартное отклонение(σ) и по формуле (1) считаем расчетное значение - критерия.

В отдельную ячейку заносим критическое значение этого критерия( в нашем случае критическое значение критерия S_крит= 3,082)

Расчётные формулы для определения выбросов

Делаем проверку для каждого значения от большего к меньшему, пока не дойдём до вывода «не выброс»

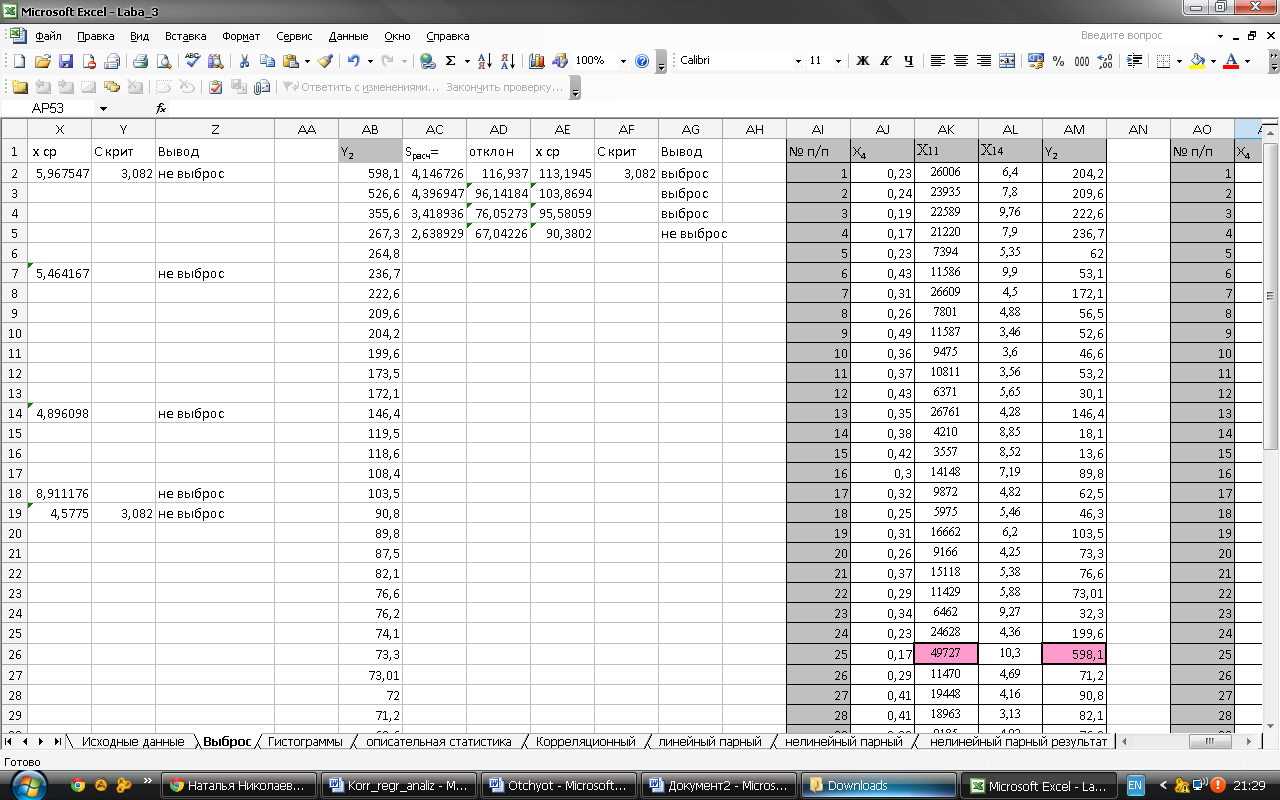
Проверка на выброса результативного признака У₂ (от большего к меньшему)

То же самое делаем для значений от меньшего к большему

Проверка на выброса результативного признака У₂ (от меньшего к большему)

Такую же проверку проводим для значений факторных признаков и получаем следующие результаты:

Проверка на выброса факторного признака Х₄ (от большего к меньшему)

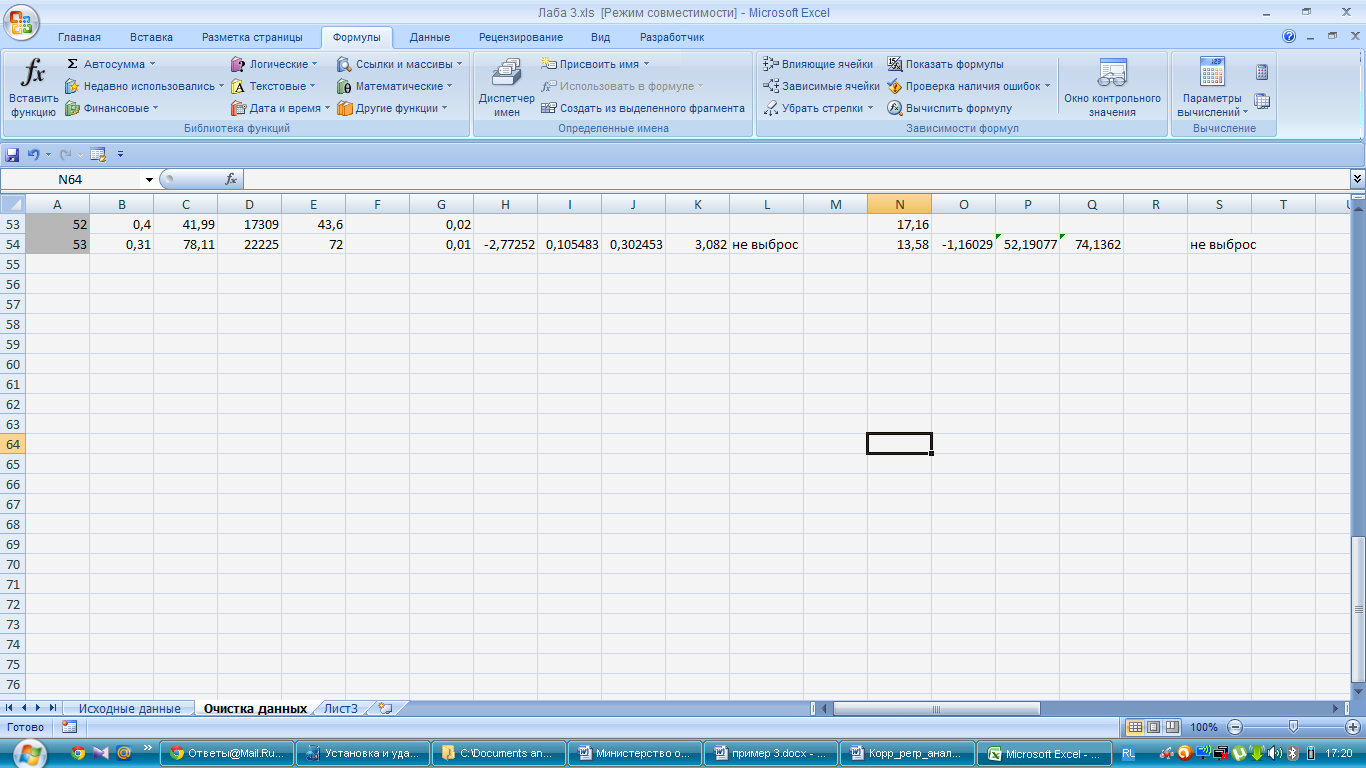
Проверка на выброс значений факторного признака Х₄ (от меньшего к большему)

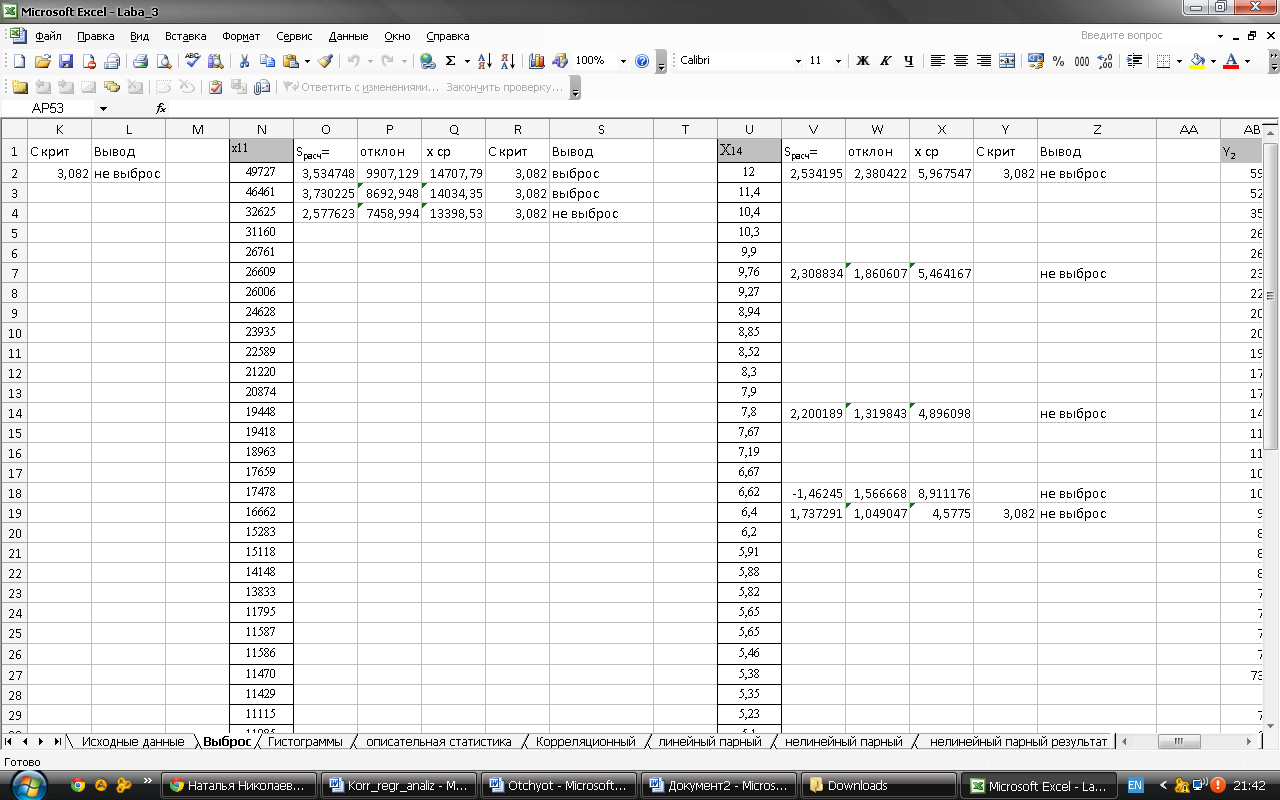
. Проверка на выброса факторного признака Х₁₁

Проверка на выброса факторного признака Х₁₄

Далее отмечаем значения, которые подлежат выбросу.

Выбросу подлежит вся строка, где есть 1 и больше значений «выброса».

Таким образом мы получаем таблицу:

Таблица с отметкой значений, подлежащих выбросу

Таким образом выбросу из выборки подлежат предприятия значения признаков которых находятся под порядковыми номерами 25,37,39.Так, как эти строки содержат сомнительную информацию. Возможно, что специалисты разных предприятий используют различные формулы для расчета показателей производственно-хозяйственной деятельности. Кроме того, могут быть просто описки, которые тоже являются грубыми ошибками. Но в любом случае включать их в корреляционно-регрессионный анализ нельзя.