
- •5.Диагональ матрица
- •1. Матрицалардың санға көбейтіндісі.
- •11. Екінші ретті анақтауыштың анықтамасы және есептелінілуі?Екінші ретті матрицаның анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады:
- •14. Элементінің алгебралық толықтауышы дегеніміз не? элементінің алгебралық толықтауышы деп мынадай санды айтады:
- •18.Кері матрица? Кері матрицаның анықтамасы
- •24. Вектордың ұзындығының формуласы.
- •26. Коллинеар векторлар.
- •28. Векторларға қолданылатын сызықтық амалдар. Векторларға қолданылатын сызықтық амалдар
- •29. Векторлардың коллинеарлығының қажетті және жеткілікті шарттары.
- •30. Сызықтық тәуелді және тәуелсіз векторлар.Векторлардың сызықтық тәуелділігі. Базис
- •34. Координаттарымен берілген векторларға амалдар қолдану. Координаттарымен берілген векторларға амалдар қолдану
- •36. Кесіндінің ортасын табу формуласы.
- •40. Жазықтықтағы түзулердің әртүрлі теңдеулері. Жазықтықтағы түзудің теңдеулері
- •1. Берілген нүктеден берілген векторға перпендикуляр өтетін түзудің теңдеуі
- •2. Түзудің жалпы теңдеуі
- •6. Берілген нүктеден өтетін түзудің теңдеуі
- •43. Нүктеден түзуге дейінгі қашықтық. 6. Нүктеден түзуге дейінгі қашықтық
- •44. Жазықтықтың әртүрлі теңдеулері. 1. Берілген нүкте арқылы, берілген векторға перпендикуляр өтетін жазықтықтың теңдеуі
- •2. Жазықтықтың жалпы теңдеуі
- •4. Жазықтықтың кесінділік теңдеуі
- •46. Екі жазықтықтың параллельдік және перпендикулярлық шарттары.
- •47. Нүктеден жазықтыққа дейінгі қашықтық.
- •48. Кеңістіктегі түзудің әртүрлі теңдеулері.Екі нуктенін ара қашықтығы
- •55. Аралықта өсетін және кемитін функциялар. 2. Аралықта өсетін және кемитін функциялар
- •56. Жұп және тақ функциялар. 3. Жұп және тақ функциялар.
- •61. Функцияның нүктедегі шегі.Анықтама.
- •62. Функцияның ақырсыздықтағы шегі.Ақырсыз аз және ақырсыз үлкен функциялар
- •1) Болса -ға қарағанда жоғары ретті ақырсыз аз деп;
- •2) Болса мен бірдей ретті ақырсыз аз деп;
- •3) Болса мен эквивалентті ақырсыз аз деп
- •64. Шектер туралы негізгі теоремалар.Шек ұғымы, біржақты шектер
- •79. Анықталған интегралдың қолданылуы.Жазық фигураның ауданын табу.
- •3. Қисық доғасының ұзындығы
34. Координаттарымен берілген векторларға амалдар қолдану. Координаттарымен берілген векторларға амалдар қолдану
![]() ,
,
![]() болса,
болса,
![]()
![]()
35.
Кесіндіні берілген қатынаста бөлу
формулалары.
Кесіндіні берілген қатынаста бөлу.
![]() және
және
![]() нүктелері арқылы өтетін кесінді
берілсін. Осы кесіндіні
қатынасындай етіп бөлетін
нүктелері арқылы өтетін кесінді
берілсін. Осы кесіндіні
қатынасындай етіп бөлетін
![]() нүктесінің координаттары:
нүктесінің координаттары:
![]() ,
,
![]() ,
,
![]() - кесіндіні
берілген қатынаста бөлу формулаларымен
анықталады.
Егер
- кесіндіні
берілген қатынаста бөлу формулаларымен
анықталады.
Егер
![]() болса, яғни
болса, яғни
![]() онда
онда
![]() ,
,
![]() ,
,
![]() - кесіндінің
ортасын табу формуласы.
- кесіндінің
ортасын табу формуласы.
36. Кесіндінің ортасын табу формуласы.
Жазықтықта
 және
және
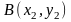 екі нүкте берілсін. АВ
кесіндісін АМ:МВ=
болатындай қатынаспен бөлетін
М(х,у)
нүктесінің координаталары мынадай
формуламен есептелінеді:
екі нүкте берілсін. АВ
кесіндісін АМ:МВ=
болатындай қатынаспен бөлетін
М(х,у)
нүктесінің координаталары мынадай
формуламен есептелінеді:
 ,
,
 .
Дербес жағдайда, АВ кесіндісін тең
екіге бөлу керек болса, яғни
=1:1=1,
формула
былай түрленеді:
.
Дербес жағдайда, АВ кесіндісін тең
екіге бөлу керек болса, яғни
=1:1=1,
формула
былай түрленеді:
 ,
,
 .Егер1болса,
яғни AN
NB
онда
.Егер1болса,
яғни AN
NB
онда
;
 ;
;
 -кесіндінің
ортасын табу формуласы.
-кесіндінің
ортасын табу формуласы.
37.
Векторлардың скалярлық көбейтіндісі.Екі
вектордың скаляр
көбейтіндісі
деп осы векторлардың ұзындықтары мен
олардың арасындағы бұрыштың косинусына
көбейтіндісіне тең шаманы айтады:
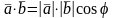 .
.
Т ік
бұрышты декарт координаталар жүйесінде
векторының басы мен соңының координаталары
белгілі болсын
ік
бұрышты декарт координаталар жүйесінде
векторының басы мен соңының координаталары
белгілі болсын
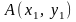 және
және
 .
Сонда
векторын координаталары арқылы былай
жазуға болады:
=
.
Сонда
векторын координаталары арқылы былай
жазуға болады:
=
 векторының басы координаталар басымен
беттесетіндей етіп өз-өзіне параллель
көшірсек, онда
векторының координатасы вектордың
соңының координаталарымен бірдей
болатынын аңғару қиын емес. Жазықтықта
вектордың координатасын екі сан
анықтаса, айталық
векторының басы координаталар басымен
беттесетіндей етіп өз-өзіне параллель
көшірсек, онда
векторының координатасы вектордың
соңының координаталарымен бірдей
болатынын аңғару қиын емес. Жазықтықта
вектордың координатасын екі сан
анықтаса, айталық
 ,
кеңістікте үш сан анытайды,
.
,
кеңістікте үш сан анытайды,
.
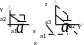
Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең: . және векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады: .Ал векторын санға көбейту мынадай түрде анықталады: . және векторларының скаляр көбейтіндісі мынадай:
Анықтама.
Екі
![]() және
және![]() векторларының
скалярлық
көбейтіндісі
деп
векторларының
скалярлық
көбейтіндісі
деп
![]() санын айтады. Скаляр көбейтінді
санын айтады. Скаляр көбейтінді
![]() ,
,
![]() ,
,
![]() символдармен белгіленеді. Мұндағы
символдармен белгіленеді. Мұндағы
![]()
![]() (
),
болғандықтан
(
),
болғандықтан
![]() деп жазуға болады.
деп жазуға болады.
4-мысал.
Егер
![]() ,
,
![]() ,
,
![]() ,
онда
,
онда
![]()
Теорема.![]() базисінде
векторының координаталары
базисінде
векторының координаталары
![]() ,
ал
векторының координаталары
,
ал
векторының координаталары
![]() болсын. Онда
болсын. Онда
![]() .
.
5-мысал.
Егер
,
![]() болса, онда
болса, онда
![]()
Скалярлық көбейтіндінің қолданылуы
1.
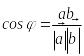 немесе
немесе
![]()
2.
![]()
![]()
![]()
3.
 (
(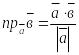 )
немесе
)
немесе
![]()
38.
Векторлардың векторлық
көбейтіндісі.
Анықтама.
және
векторларының векторлық
көбейтіндісі
деп, келесі үш шартты қанағаттандыратын
![]() векторын
айтады:
векторын
айтады:
1)
![]() ;
;
2)
![]() векторының
ұзындығы
және
векторларына тұрғызылған параллелограммның
ауданына тең, яғни
векторының
ұзындығы
және
векторларына тұрғызылған параллелограммның
ауданына тең, яғни
![]() ,
мұндағы
;
,
мұндағы
;
3)
![]() векторлары оң үштік құрайды.
векторлары оң үштік құрайды.
Векторлық
көбейтінді
![]() немесе
немесе
![]() деп белгіленеді.
деп белгіленеді.
Векторлық
көбейтіндінің анықтамасынан
![]() ,
,
![]() ,
,
![]() болады
болады
Векторлық көбейтіндінің қолданылуы
1.
![]() ,
,
![]()
2.
Егер
||
болса, онда
![]() (және
керісінше)
(және
керісінше)
39.
Векторлардың аралас көбейтіндісі.
Анықтама.
векторларының аралас көбейтіндісі
деп,
және
векторларының векторлық көбейтіндісі
мен
![]() векторының
скаляр көбейтіндісін айтады.
векторының
скаляр көбейтіндісін айтады.![]()
Аралас
көбейтінді
![]() не
не
![]() немесе
немесе
![]() түрінде жазылады. Аралас көбейтіндінің
нәтижесі санға тең.
түрінде жазылады. Аралас көбейтіндінің
нәтижесі санға тең.
Аралас көбейтіндінің қасиеттері:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
Егер векторлар
компланар болса, онда
![]() .
.
Теорема.
базисінде
![]() ,
,
![]() ,
,
![]() векторлары берілсін, онда олардың
аралас көбейтіндіні анықтауыш түрінде
жазуға болады.
векторлары берілсін, онда олардың
аралас көбейтіндіні анықтауыш түрінде
жазуға болады.
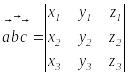
Аралас көбейтіндінің қолданылуы
Егер
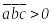 болса, онда
-оң
үштік; егер
болса, онда
-оң
үштік; егер
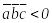 болса, онда
-
сол үштік құрайды.
болса, онда
-
сол үштік құрайды.
векторлары компланар.
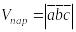 ,
,
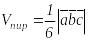 .
.
