26. Коллинеар векторлар.

Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды немесе , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( = , , а). векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады, = және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады. және векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

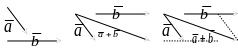
және векторларының - айырымы деп -ға қосқанда векторы алынатын = - векторын айтады.

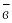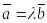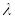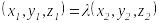
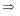
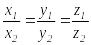• || болғандықтан оны деп жазуға болады, мұндағы - қайсыбір сан. Осыдан -екі вектордың коллинеарлығының белгісі.

27. Компланар векторлар.Векторлардың компланарлық шарты а, в, с векторлардың бас нүктелерін бір нүктеге түйістіргенде олар бір жазықтықта орналасса онда ол векторлар компланар болады. Белгісі: а = в + с. Егер векторлар координаталарымен берілсе, яғни а (х1, у1, Z1), в (х2, у2, Z2), с (х3, у3, Z3) болса, онда олардың компланарлық белгісі:

х1 у1 Z1

х2 у2 Z2 = 0

х3 у3 Z3

Мысалдар: 1) а = i – j + 2, в= 3i +j,

c= mi + 2kвекторлары компланар болатындай m мәнін тап.

1 - 1 2

3 1 0 = 2 - 2m + 6 = 0 = m = 4, = а = gв + pс орындала ма, тексерейік; а (1; -1, 2) = g (3,

M0 2 1, 0) + р (4, 0, 2) = 1 = 3g + 4р

-1 = g + 0 =

2 = 0 + 2р

= g = -1 = а = -в + с, яғни векторлар компланар.

р = 1

Үш вектордың компланар бояу шарты

 

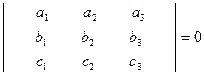 (42)

 

формуламен, ал   векторлар қыры болатын параллепипед көлемi.

 

 (43)

 

формуламен, ал бiр төбеден шығатын қырлары   болатын тетраэдрдiң көлемi.

 

 (44)

формуламен табылады.

28. Векторларға қолданылатын сызықтық амалдар. Векторларға қолданылатын сызықтық амалдар

Сызықтық амалдар деп, векторларды қосу және алу, векторды санға көбейту амалдарын айтады.Екі вектордың қосындысын екі жолмен табуға болады: бірі параллелограмм әдісі, екіншісі үшбұрыштар әдісі.

Параллелограмм әдісі. және векторларының қосындысы деп, және векторларының ортақ бас нүктесінен шығатын, параллелограммның диагоналіне сәйкес келетін векторды айтады.

Үшбұрыштар әдісі.Егер векторының басы векторының ұшына орналасса, онда және векторларының қосындысы деп, векторының басы мен векторының ұшын қосатын векторды айтады.

Бір нүктеден шығатын және векторларының айырымы деп векторының ұшын векторының ұшымен қосатын векторды айтады.

векторының санына көбейтіндісі деп ұзындығы -ға тең, векторына коллинеар, егер болса векторымен бағыттас және болса, векторына қарама-қарсы бағытталған векторын айтады. және векторларының коллинеарлығының қажетті және жеткілікті шарты: