47. Нүктеден жазықтыққа дейінгі қашықтық.

Нүктеден түзуге дейінгі қашықтық. нүктесінен түзуіне дейінгі қашықтықтың формуласы:

(4.9)

2-мысал. нұктесінен тұзуіне дейінгі қашықтықты табу керек.

48. Кеңістіктегі түзудің әртүрлі теңдеулері.Екі нуктенін ара қашықтығы

Жазықтықта және екі нүкте берілсін. Осы екі нүкте арақашықтығын, немесе АВ кесіндісінің ұзындығын, мына формуламен есептейді:

.

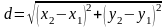Түзудің жалпы теңдеуі

(4.1) теңдеуінде жақшаларды ашып, деп белгілесек, түзудің жалпы теңдеуі шығады

(4.2)

Егер А=0 болса, онда түзу Ох өсіне параллель өтеді; егер В=0 болса, онда түзу Оу өсіне параллель өтеді; егер С=0 болса, онда түзу жүйенің бас нүктесі арқылы өтеді.

Нүктеден түзуге дейінгі қашықтық. нүктесінен түзуіне дейінгі қашықтықтың формуласы:

(4.9)

2-мысал. нұктесінен тұзуіне дейінгі қашықтықты табу керек.

Екі нүкте арқылы өтетін түзудің теңдеуі. Түзу және нүктелерінен өтсін. Түзудің бойынан кез келген нүктесін аламыз. Сонда бұл түзудің теңдеуі төмендегідей болады:

Екі түзудің арасындағы бұрыш. және түзулерінің арасындағы бұрыштың формуласы:

(4.7)

Осыдан егер түзулер параллель болса, онда , ал түзулер перпендикуляр болса, онда болады. Түзулер және теңдеулерімен берілсе, онда , болғандықтан түзулердің арасындағы бұрыш осы екі нормальдің арасындағы бұрышқа тең:

(4.8)

Осыдан егер түзулер параллель болса, онда , ал перпендикуляр болса, онда болады.

_{49. Түзу мен жазықтықтың өзара орналасуы.}Кеңістіктегі түзудің орны осы түзуде жататын бір   нүктесі және осы түзуге параллель   векторы арқылы анықталады. Кеңістіктегі осы түзудің теңдеуін қорытып шығарамыз. Түзудің теңдеуін құру үшін түзудің бойынан кез келген ағымдағы координаталарымен   нүктесін аламыз да М₀ және М нүктелерін координаталарымен   саламыз да М₀ және М нүктелерін координаталар басымен қосамыз және координаталарын табамыз:

 болатыны суерттен көрініп тұр. Егер М нүктесі түзу бойынд жататын болса, онда   және   векторлары коллинеарт болады. Ендеше, бұл векторлар   коллинеарлық шартын қанағаттандырады, мұндағы t - параметр.

Векторлардың коллинеарлық шартын   (1) түрінде жазамыз, бұл түзудің векторлық теңдеуі.

(1) түзудің векторлық теңдеуі,   нүктесі мен бағыттаушы   векторының координаталары берілсін.

(1) теңдеудің сол жағын векторлық түрде жазамыз

және бағыттаушы вектор

Сонда (1) теңдеу мына түрге келеді:

Теңдіктің оң және сол бөліктеріндегі бірлік векторлардың сәйкес коэффициенттерін теңестіріп, түзудің параметрлік теңдеуін аламыз.

 немесе   (2)

(2)- параметрлік теңдеу.

(2) теңдеудегі t параметрінен құтылып, түзудің канондық теңдеуін аламыз:

 (3)

Мысал.   нүктесінен өтетін және   векторына параллель түзудің канондық және параметрлік теңдеуін құру керек.

(3): 

(2): 

Кеңістіктегі түзудің жалпы теңдеуі. Кеңістікте түзу екі жазықтықтың қиылысуымен анықталатын болғандықтан, онда оның кеңістіктегі жалпы теңдеуі

(4)

жүйесі түрінде өрнектеледі, мұндағы бірінші және екіні теңдеулер сәйкес жазықтықтар теңдеулері.

50. Эллипстің канондық теңдеуі.. Эллипс

Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды.

Анықтама бойынша , мұндағы және - фокустар деп аталатын берілген нүктелер, -эллипстің бойындағы кез келген нүкте, -тұрақты шама.

Егер десек, онда , . Енді осы мәндерді теңдеуіне қойып, түрлендіріп, эллипстің канондық теңдеуін аламыз:

(6.3)

мұндағы эллипстің үлкен жарты өсі, оның кіші жарты өсі болады. ны табу үшін эллипстің бойынан нүктесін аламыз. болғандықтан немесе болады. Пифагор теоремасы бойынша . Осыдан деп белгілейміз. қатынасын эллипстің эксцентриситеті деп атайды. болғандықтан . эллипстің директрисаларының теңдеуі. Ол эллипстің сыртында жатады.

51. Гиперболаның канондық теңдеуі.Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырмасының абсолюттік шамасы тұрақты 2а-ға тең болатын жазықтықтағы нүктелердің геометриялық орындарын гипербола деп атайды.

Гиперболаның канондық теңдеуі былай жазылады:

(6.4)

Мұндағы , - гиперболаның нақты жарты өсі, жорымал жарты өсі, гиперболаның эксцентриситеті, болғандықтан . Егер гиперболаның нүктесі шексіздікке ұмтылғанда нүктесінен түзуге дейінгі қашықтық нөлге ұмтылса, онда мұндай түзуді гиперболаның асиптотасы дейді. Гиперболаның асимптоталарының теңдеулері: және , мұндағы және гиперболаның жарты өстері. гиперболаның директрисаларының теңдеуі. Гиперболаның директрисалары оның төбелерінің арасында жатады

52. Параболаның канондық теңдеуі.. Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды.

Анықтама бойынша , мұндағы және - фокустар деп аталатын берілген нүктелер, -эллипстің бойындағы кез келген нүкте, -тұрақты шама.

Егер десек, онда , . Енді осы мәндерді теңдеуіне қойып, түрлендіріп, эллипстің канондық теңдеуін аламыз:

(6.3)

мұндағы эллипстің үлкен жарты өсі, оның кіші жарты өсі болады. ны табу үшін эллипстің бойынан нүктесін аламыз. болғандықтан немесе болады. Пифагор теоремасы бойынша . Осыдан деп белгілейміз. қатынасын эллипстің эксцентриситеті деп атайды. болғандықтан . эллипстің директрисаларының теңдеуі. Ол эллипстің сыртында жатады.

53. Екінші ретті беттердің канондық теңдеулері.Екінші ретті беттер деп, координаталар жүйесінде екінші дәрежелі теңдеулермен берілетін беттерді айтады.

Екінші ретті беттердің қасиеттері техникада, құрылыс негіздерінің конструкцияларында сонымен бірге күн сәулесінің қуатын от қуатына айналдыру мақсатында қолданылады.

Мысалы, шағылыстыру айналары, түрлі прожекторлар параболоидтың қасиеттеріне, ал бір қуысты гиперболоидтың түзу сызықты жасаушылары болу қасиеттерін құрылыста қолданады. Ал сфералық айналарды қолданып, өмірдің түрлі қажетіне пайдаланады.

1. Сфера. Бекрілген нүктеден бірдей қашықтықта орналасқан

кеңістіктегі нүктелердің геометриялық орындарын сфералық немесе шар беті деп атайды .Егер сфераның центрі С(a,b,c) нүктесі және оның бетіндегі кез келген нүкте жылжымалы нүктесі M(x,y,z) болса, онда анықтама бойынша CM=R , R-сфераның радиусы.

Кеңістіктегі екі нүктенің арасындағы қашықтықтың формуласы бойынша

немесе - сфераның канондық теңдеуі.

2.Цилиндр. Цилиндр перпендикулчрлық қимасындағы сызықтың түріне қарай төрт түрге бөлінеді: дөңгелек, эллипстік, гиперболалық, және парболалық цилиндр болып, осыған сәйкес цилиндр тік бұрышты координаталар жүйесінде төрт түрлі теңдеумен анықталады:Бұл төрт теңдеу жазықтықта шеңберді, эллипсті, гиперболаны және паболаны кескіндейді, ал кеңістікте дөңгелек, эллипстік, гиперболалық және параболалық цилиндрлейді кескіндейді.Сонымен цилиндр (цилиндрлік бет) дегеніміз шеңбер, элллипс, гипербола, параболалардың бойымен олардың жазықтықтарына перпендикуляр болып өтетін түзу сызықтардың үздіксіз қозғалысынан шығатын екінші ретті беттер.Осы шеңбер, эллипс, гипербола, және парабола цилиндрлердің бағыттаушылары, ал цилиндрдің беттерінде жатқан түзулер олардың жасаушылары деп аталады.

3.Конус. Конус деп берілген нүктеден өтетін және бағыттаушы қисықтың бойымен жылжитын жасаушы түзудің үздіксіз қозғалысынан шығатын бетті айтады.

Конустың бағыттаушысы эллипс, ал жасаушы түзуі координаталардың бас нүктесінен өтсін. Сонда конустың теңдеуі:

болады.Мұндағы z=c конусты XOY жазықтығына параллель қиып өтетін жазықтық. Ал егер a=b болса, онда конустың перпендикулярлық қимасы шеңбер болады:

- айнымалы концстың теңдеуі. Төбесі координаталардың бас нүктесінде апликата осіне симметриялы екінші ретті конустық беттің теңдеуі.4.Айналу беттері. Егер кеңістікте бір сызық берілген осьті айналса, оның айналуынан бет п.б.Айналушы сызықтың формасына байланысты бет әр түрлі болады. Мысалы, егершеңберөзініңдиаметрібойыншаайналса, сфералық бет шығады, ал координаталарбасынанөтетінтүзу OZ осінайналса, дөңгелек конус п.б. Сызықтыңайналатыносінайналуосі, ал пайдаболғанбеттіайналубетідепатайды.Бізге YOZ жазықтығындажатқан L сызығытеңдеуіменберілсін. Осы сызықтың OY осінайналғандапайдаболғанбеттіңтеңдеуін табу үшінсолсызықтыңтеңдеудегі y – тіөзгертпей, z – тіөрнегіменалмастырукерек. Сонда айналубетініңтеңдеуімынандайболады:Басқаосьтердіайналғандапайдаболғанбеттердің де теңдеулеріосығанұқсастабылады. Яғни, егерберілгенсызық OZ осіненайналса, ондаайналубетініңтеңдеуіболады.

5. Айналу эллипсоиды.Үшосьті эллипсоид. YOZ жазықтығындатеңдеулеріменберілгенэллипсті OZ осіменайналдырғаннаншыққанбеттіайналу эллипсоид депатайды.6. Бірқуысты гиперболоид. Бізге YOZ жазықтығындаорналасқан гипербола теңдеуіменберілсін.

Осы гиперболаны OZ осіненайналдырсақбірқуысты гиперболоид депаталатынайналубетішығады. Оныңтеңдеуі

болады.

Осы айналугиперболоидындеформацияласақ, яғни

десек, ондамынатүргекеледі:

Осы теңдеуменанықталатынбеттібірқуысты гиперболоид депатайды. Айнымалыбірқуыстыгиперболоидтыңбірқуыстыгиперболоидтанайырмашылығыоның XOZ жазықтығына параллель жазықтықпенқимасы эллипс емесшеңберболады.

Екінші ретті қисықтың жалпы теңдеуі

Теорема. (6.6) теңдеуі әрқашан не шеңберді (егер ), не эллипсті (егер ), не гиперболаны (егер ), не параболаны (егер ) анықтайды. Бұл жағдайларда эллипс (шеңбер) нүктеге немесе жорымал эллипске (шеңберге), гипербола қиылысатын түзулердің жұбына, парабола параллель түзулердің жұбына айналуы мүмкін.

1-мысал. теңдеуін канондық түрге келтіру керек.

эллипстің теңдеуі.

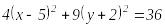
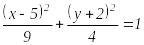• Осыдан 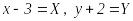деп белгілесек 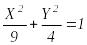эллипстің канондық теңдеуі, Бұл жүйенің басы 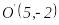нүктесінде орналасқан.

54. Функцияның анықтамасы.Функция немесе функциялық тәуелділік ұғымы түрлі шамалар, экономикалық көрсеткіштер арасындағы байланыстарды моделдейтін математиканың маңызды ұғымы.

Анықтама. Х жиынының әрбір х элементіне ( ) белгілі бір заң немесе ереже бойынша У жиынының у элементі сәйкес қойылса, онда Х жиынында функция берілген деп атайды. хжәнеушамаларының арасындағы функциялық тәуелділікті y=f(x) деп белгілейді, мұндағы х - аргумент(тәуелсіз айнымалы), у – функция(тәуелді айнымалы), f – ереже немесе заң.

Берілген функция анықталатын х аргументтерінің жиынын функцияның анықталу облысы деп, ал сәйкес у айнымалылардың жиынын функцияның мәндер жиыны деп атайды. Әдетте анықталу облысын D(f) деп, ал мәндер жиынын E(f) деп белгілейді.

Функция түрлі тәсілдермен берілуі мүмкін. Ең көп және маңызды берілу түрлері: аналитикалық(формула түрінде), кестелік және графиктік. Мысал ретінде заттың бағасы (р) мен сол затқа деген сұраныс (q) арасындағы байланысты қарастырайық:

р (теңге)	100	150	200	250	300	...
q (мың дана)	18	15	12	9	6	...

Кестеден көрініп тұрғандай, заттың бағасы артқан сайын, оған деген сұраныс төмендейді екен. Бұл байланысты графиктік түрде де беруге болады.

Заттың бағасы мен сұраныс арасында түзу сызықты p=kq+b байланыс байқалады. Берілген мәндерді пайдаланып бұл байланысты табу қиын емес: .

Кестенің төменгі жолындағы сұраныстың мәндерін q орнына қойсақ жоғары жолдағы бағаның сәйкес мәндері шығып отырады. Сонымен, функцияның аналитикалық берілуінен оның кестелік және графиктік түрлерін оңай алуға болады екен.