
- •5.Диагональ матрица
- •1. Матрицалардың санға көбейтіндісі.
- •11. Екінші ретті анақтауыштың анықтамасы және есептелінілуі?Екінші ретті матрицаның анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады:
- •14. Элементінің алгебралық толықтауышы дегеніміз не? элементінің алгебралық толықтауышы деп мынадай санды айтады:
- •18.Кері матрица? Кері матрицаның анықтамасы
- •24. Вектордың ұзындығының формуласы.
- •26. Коллинеар векторлар.
- •28. Векторларға қолданылатын сызықтық амалдар. Векторларға қолданылатын сызықтық амалдар
- •29. Векторлардың коллинеарлығының қажетті және жеткілікті шарттары.
- •30. Сызықтық тәуелді және тәуелсіз векторлар.Векторлардың сызықтық тәуелділігі. Базис
- •34. Координаттарымен берілген векторларға амалдар қолдану. Координаттарымен берілген векторларға амалдар қолдану
- •36. Кесіндінің ортасын табу формуласы.
- •40. Жазықтықтағы түзулердің әртүрлі теңдеулері. Жазықтықтағы түзудің теңдеулері
- •1. Берілген нүктеден берілген векторға перпендикуляр өтетін түзудің теңдеуі
- •2. Түзудің жалпы теңдеуі
- •6. Берілген нүктеден өтетін түзудің теңдеуі
- •43. Нүктеден түзуге дейінгі қашықтық. 6. Нүктеден түзуге дейінгі қашықтық
- •44. Жазықтықтың әртүрлі теңдеулері. 1. Берілген нүкте арқылы, берілген векторға перпендикуляр өтетін жазықтықтың теңдеуі
- •2. Жазықтықтың жалпы теңдеуі
- •4. Жазықтықтың кесінділік теңдеуі
- •46. Екі жазықтықтың параллельдік және перпендикулярлық шарттары.
- •47. Нүктеден жазықтыққа дейінгі қашықтық.
- •48. Кеңістіктегі түзудің әртүрлі теңдеулері.Екі нуктенін ара қашықтығы
- •55. Аралықта өсетін және кемитін функциялар. 2. Аралықта өсетін және кемитін функциялар
- •56. Жұп және тақ функциялар. 3. Жұп және тақ функциялар.
- •61. Функцияның нүктедегі шегі.Анықтама.
- •62. Функцияның ақырсыздықтағы шегі.Ақырсыз аз және ақырсыз үлкен функциялар
- •1) Болса -ға қарағанда жоғары ретті ақырсыз аз деп;
- •2) Болса мен бірдей ретті ақырсыз аз деп;
- •3) Болса мен эквивалентті ақырсыз аз деп
- •64. Шектер туралы негізгі теоремалар.Шек ұғымы, біржақты шектер
- •79. Анықталған интегралдың қолданылуы.Жазық фигураның ауданын табу.
- •3. Қисық доғасының ұзындығы
1.Матрицаның анықтамасы? Матрицадеп, m- жол және n- бағаннан тұратын сандар немесе әріптерден құрылған тік бұрышты кестені айтады.
Анықтама. m жатық n тік жолдан құрылған кестені mxn өлшемді матрица деп атайды.
Матрицаны құрайтын сандар матрица элементтері деп аталады. Әдетте матрица латын алфавитінің бас әріптерімен, ал элементтері сәйкес кіші әріптермен белгіленеді:
Қысқаша
жазылуы:
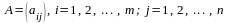
Матрица
элементінің бірінші индексі жатық жол
нөмірі, ал екінші индексі тік жол
(бағана) нөмірін көрсетеді. Мысалы,
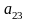 элементі екінші жатық жол мен үшінші
тік жол қиылысында орналасқан. Бір ғана
жатық жолдан құралған матрицаны
жол-матрица,
ал бір
ғана тік жолдан құралған матрицаны
бағана-матрица
депатайды:
элементі екінші жатық жол мен үшінші
тік жол қиылысында орналасқан. Бір ғана
жатық жолдан құралған матрицаны
жол-матрица,
ал бір
ғана тік жолдан құралған матрицаны
бағана-матрица
депатайды:
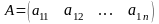 - жол-матрица;
- жол-матрица;
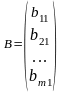 -
бағана матрица.
-
бағана матрица.
Жол матрица мен бағана матрицаны кейде вектор деп те айтады.. Жатық жолдар саны мен тік жолдар саны тең болатын матрица квадрат матрица деп аталады,

Квадрат
матрицаның
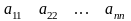 элементтері диагоналдық
элементтер деп
аталады да, матрицаның негізгі
диагоналін құрайды.
Ал
элементтері диагоналдық
элементтер деп
аталады да, матрицаның негізгі
диагоналін құрайды.
Ал
 элементтері
қосымша
диагоналдық элементтер деп
аталады да, матрицаның қосымша
диагоналін құрайды.
Квадрат матрицаның негізгі диагоналінің
астындағы немесе үстіндегі элементтері
нолге тең болса, матрица үшбұрышты
матрица
деп аталады,
элементтері
қосымша
диагоналдық элементтер деп
аталады да, матрицаның қосымша
диагоналін құрайды.
Квадрат матрицаның негізгі диагоналінің
астындағы немесе үстіндегі элементтері
нолге тең болса, матрица үшбұрышты
матрица
деп аталады,
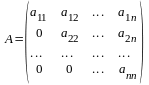 ,
,
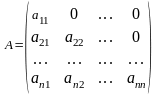
Диагоналды емес элементтерінің бәрі нолге тең болатын квадрат матрица диагоналды матрица деп аталады,
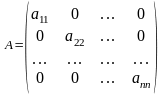 .
.
Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,
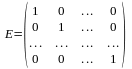 .
Барлық
элементтері нолге тең матрица нолдік
матрицадеп
аталады.
.
Барлық
элементтері нолге тең матрица нолдік
матрицадеп
аталады.
2. Жол матрица дегеніміз не?Бір ғана жатық жолдан құралған матрицаны жол-матрица, ал бір ғана тік жолдан құралған матрицаны бағана-матрица деп атайды: - жол-матрица;
3.Баған матрица? - бағана матрица.
Бір бағаннан тұратын матрицаны баған-матрица дейді.
4.Квадрат
матрица?Егер
матрицаның жолдарының саны бағандарының
санына тең болса, ондай матрицаны
квадрат
матрицадейді.
Оның өлшемі
![]() болады.
болады.
Квадрат матрицаның элементтері диагоналдық элементтер деп аталады да, матрицаның негізгі диагоналін құрайды. Ал элементтері қосымша диагоналдық элементтер деп аталады да, матрицаның қосымша диагоналін құрайды.
5.Диагональ матрица
Егер квадрат матрицаның бас диагональдан тыс элементтері нөлге тең болса, онда ондай матрицаны диагональ матрица дейді.
6.Бірлік матрица?Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,
. Барлық элементтері нолге тең матрица нолдік матрица деп аталады.
7.Үшбұрышты матрица дегеніміз не? Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,
, 8.Матрицаларға қолданылатын амалдар?Матрицаны санға көбейту. 1. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
Мысалы,
 матрицасын
матрицасын
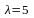 санына көбейтейік: .
санына көбейтейік: .
Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
2.Матрицаларды
қосу және алу.
2.
Матрицаларды қосу және алу.
Өлшемдері бірдей матрицаларды ғана
қосуға болады.
А және В матрицаларының қосындысы деп
элементтері осы матрицалардың сәйкес
элементтерінің қосындысы болатын, А +
В матрицаны айтамыз: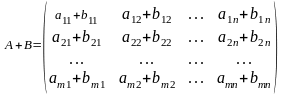 .
.
А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті:A – B = A+(-1)B немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады. Мысалы А матрицасынан В матрицасын алайық:
3.Матрицаларды көбейту. 3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі mxk болатын А матрицасы мен өлшемі kxn болатын В матриасы берілсін:
Осы екі матрицаны көбейткенде өлшемі mxn болатын көбейтінді С матрица аламыз:
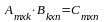
С
матрицасының
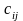 элементі А
матрицаның
элементі А
матрицаның
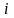 –жатық
жол элементтерін В
матрицаның
–жатық
жол элементтерін В
матрицаның
 –тік
жолының сәйкес элементтеріне көбейтіп
қосқанға тең болады:
–тік
жолының сәйкес элементтеріне көбейтіп
қосқанға тең болады:
 ,
,
 .
(1) Мысалы,
.
(1) Мысалы,
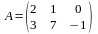 матрицасы мен
матрицасы мен
 матрицасын көбейтейік. Бірінші матрица
үш тік жолдан, ал екінші матрица үш
жатық жолдан тұрғандықтан бұл матрицаларды
көбейтуге болады. Көбейтінді матрицаның
өлшемін анықтайық:
матрицасын көбейтейік. Бірінші матрица
үш тік жолдан, ал екінші матрица үш
жатық жолдан тұрғандықтан бұл матрицаларды
көбейтуге болады. Көбейтінді матрицаның
өлшемін анықтайық:
 ,
яғни,
,
яғни,
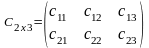 .
k=3
болғандықтан (1) формуланы қолданғанда
үш қосылғыш болады:
.
k=3
болғандықтан (1) формуланы қолданғанда
үш қосылғыш болады:
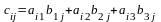 ,
,
 .
.
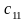 элементін табу үшін формуладағы i=1,
j=1 деп
аламыз, сонда
элементін табу үшін формуладағы i=1,
j=1 деп
аламыз, сонда
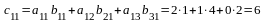 ,
яғни А
матрицаның 1-жатық жол элементтерін В
матрицаның 1-тік жолының сәйкес
элементтеріне көбейтіп қостық. Осылай
С матрицаның барлық элементтері
табылады:
,
яғни А
матрицаның 1-жатық жол элементтерін В
матрицаның 1-тік жолының сәйкес
элементтеріне көбейтіп қостық. Осылай
С матрицаның барлық элементтері
табылады:
C=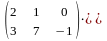
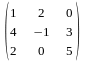 =
=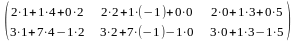 =
=
=
= .
.
Қосу және көбейту амалдарының мынадай қасиеттері бар:
1) A+B=B+A |
5) (A+B)C=AC+BC |
2) (A+B)+C=A+(B+C) |
6)
|
3) (A+B)= A+ B |
7) A(BC)=(AB)C |
4) A(B+C)=AB+AC |
|
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық.
8)
Біріншіден, екі матрицаның АВ
көбейтіндісі болғанмен ВА
көбейтіндісі болмауы мүмкін. Мысалы,
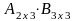 көбейтіндісі бар, бірақ
көбейтіндісі бар, бірақ
 көбейтіндісі жоқ, себебі бірінші
матрицаның тік жолдар саны екінші
матрицаның жатық жолдар санына тең
емес;
көбейтіндісі жоқ, себебі бірінші
матрицаның тік жолдар саны екінші
матрицаның жатық жолдар санына тең
емес;
екіншіден,
АВ
және ВАкөбейтінділері
бар болғанмен, олардың өлшемдері әртүрлі
болуы мүмкін. Мысалы,
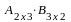 және
және
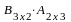 көбейтінділер бар, бірақ өлшемдері
әртүрлі:
көбейтінділер бар, бірақ өлшемдері
әртүрлі:
 ,
,
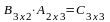 ;
үшіншіден, АВ
және ВАкөбетінділер
бар және олардың өлшемдері бірдей
болғанмен, жалпы жағыдайда, көбейтудің
коммутативті заңы орындалмайды, яғни
АВ
;
үшіншіден, АВ
және ВАкөбетінділер
бар және олардың өлшемдері бірдей
болғанмен, жалпы жағыдайда, көбейтудің
коммутативті заңы орындалмайды, яғни
АВ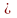 BA.
BA.
Мыс: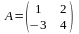 мен
мен
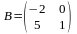 матрицалары берілген. АВ
және ВАкөбейтінділерін
табау керек. Шешуі. Берілген матрицалар
өлшемдері 2х2
квадрат матрицалар, оларды көбейтуге
болады:
матрицалары берілген. АВ
және ВАкөбейтінділерін
табау керек. Шешуі. Берілген матрицалар
өлшемдері 2х2
квадрат матрицалар, оларды көбейтуге
болады:
 .
.
 .
.
Көріп отырғанымыздай АВ BA.
9) А-квадрат матрица болса, онда мына теңдік орындалады: АЕ = ЕА = А.
9.Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері?Өлшемдері бірдей матрицаларды ғана қосуға болады. А және В матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз:
Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
Мысалы, матрицасын санына көбейтейік:Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.

 (AB)=(
A)B=A(
B)
(AB)=(
A)B=A(
B)