53. Екінші ретті беттердің канондық теңдеулері. Екінші ретті қисықтың жалпы теңдеуі

Теорема. (6.6) теңдеуі әрқашан не шеңберді (егер ), не эллипсті (егер ), не гиперболаны (егер ), не параболаны (егер ) анықтайды. Бұл жағдайларда эллипс (шеңбер) нүктеге немесе жорымал эллипске (шеңберге), гипербола қиылысатын түзулердің жұбына, парабола параллель түзулердің жұбына айналуы мүмкін.

1-мысал. теңдеуін канондық түрге келтіру керек.

эллипстің теңдеуі.

. Осыдан деп белгілесек -эллипстің канондық теңдеуі, Бұл жүйенің басы нүктесінде орналасқан.

54. Функцияның анықтамасы. Анықтама. және бос емес сандар жиындары болсын. Егер 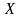жиынының кез келген элементіне белгілі бір заңдылықпен 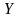жиынының бір 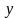элементі сәйкес келетін болса, онда жиынында функциясы берілді дейді. Мұндай жағдайда 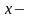ті тәуелсіз шама (аргумент), ал ті тәуелді шама деп атайды. әрпі пен жиындарының арасында сәйкестік заңдылықты береді. жиыны функцияның анықталу облысы, ал жиыны функция мәндерінің жиыны деп аталады.

Функцияның үш түрлі жолмен беріледі:

а)Аналитикалық тәсілмен;

б) Таблицалық, яғни мәндер тәсілімен;

в) Графиктік тәсілмен

Функцияның негізгі қасиеттері

1. Анықтама. Егер аралығында жатқан барлық нүктелері үшін теңсіздігі орындалатындай 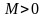саны табылса, онда 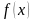функциясы аралығында шектелген функция деп аталады. Дербес жағдайда, болғанда шарты айнымалысының шектеулігін көрсетеді.

55. Аралықта өсетін және кемитін функциялар. 2. Аралықта өсетін және кемитін функциялар

Анықтама. сегментінде (аралығында) анықталған функциясы үшін , болғанда теңсіздігі орындалса, онда осы аралықта өспелі (кемімелі) функция деп аталады.

Функция аралықта өспелі немесе кемімелі болса, онда бұл аралық монотондық аралық, ал функциясы осы аралықта монотонды деп аталады.

Мысал. функциясы аралығында монотонды және: интервалында кемімелі, ал интервалында өспелі.

56. Жұп және тақ функциялар. 3. Жұп және тақ функциялар.

а) болса, - жұп функция;

б) болса, - тақ функция.

57. Периодты функциялар. Периодты функциялар. облысында анықталған фукциясы үшін саны табылып, , , теңдігі орындалса, онда периодты функция деп аталады.

58. Күрделі функция. 4. 5. Kүрделі функция . 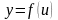функциясының анықталу облысы 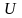, мәндер жиыны болсын, ал 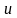айнымалысы жиынында анықталған ке тәуелді, мәндер жиыны болатын функция болсын: 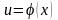. Сонда жиынында берілген, мәндер жиыны болатын функциясы күрделі функция деп аталады.

Мысалы, 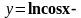күрделі функция, өйткені оны былай жазуға болады: .

59. Кері функция. . Kері функция. функциясының анықталу облысы , ал мәндер жиыны болсын. Әрбір мәніне 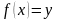теңдігі орындалатындай бір мәнін сәйкес қойсақ, онда жиынында анықталған, ал мәндер жиыны болатын 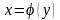функциясы анықталады. Осы функция 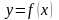функциясының кері функциясы деп аталады және ол түрінде жазылады. және функциялары өзара кері функциялар деп аталады

60. Айқындалмаған функция. 7. Белгісіз функция анық түрде берілмей, түрінде берілсе, онда тәуелділігі айқындалмаған функция деп аталады.

8. Функцияның параметрлік түрде берілуі. Егер функциясы үшін кері функция табылса, онда түрдегі тің ке тәуелді функциясын аламыз.