
- •1. Матрицалардың санға көбейтіндісі.
- •12. Үшінші ретті анақтауыштың анықтамасы және есептелінілуі? а матрицасының анықтауышы немесе 3-ші ретті анықтауышы деп, төменгі формуламен есептелінетін санды айтады:
- •20. Қандай жүйе үйлесімді деп аталады?
- •21. Қандай жүйе үйлесімсіз деп аталады?
- •24. Вектордың ұзындығының формуласы.
- •25. Вектордың орты.
- •26. Коллинеар векторлар.
- •28. Векторларға қолданылатын сызықтық амалдар. Векторларға қолданылатын сызықтық амалдар
- •29. Векторлардың коллинеарлығының қажетті және жеткілікті шарттары.
- •30. Сызықтық тәуелді және тәуелсіз векторлар. Векторлардың сызықтық тәуелділігі. Базис
- •34. Координаттарымен берілген векторларға амалдар қолдану. Координаттарымен берілген векторларға амалдар қолдану
- •36. Кесіндінің ортасын табу формуласы.
- •40. Жазықтықтағы түзулердің әртүрлі теңдеулері. Жазықтықтағы түзудің теңдеулері
- •1. Берілген нүктеден берілген векторға перпендикуляр өтетін түзудің теңдеуі
- •2. Түзудің жалпы теңдеуі
- •6. Берілген нүктеден өтетін түзудің теңдеуі
- •4. Жазықтықтың кесінділік теңдеуі
- •46. Екі жазықтықтың параллельдік және перпендикулярлық шарттары.
- •47. Нүктеден жазықтыққа дейінгі қашықтық.
- •2. Түзудің канондық теңдеуі
- •53. Екінші ретті беттердің канондық теңдеулері. Екінші ретті қисықтың жалпы теңдеуі
- •55. Аралықта өсетін және кемитін функциялар. 2. Аралықта өсетін және кемитін функциялар
- •56. Жұп және тақ функциялар. 3. Жұп және тақ функциялар.
- •61. Функцияның нүктедегі шегі. Функцияның нүктедегі шегі
- •62. Функцияның ақырсыздықтағы шегі.
- •Екінші тамаша шек:
- •79. Анықталған интегралдың қолданылуы. Жазық фигураның ауданын табу.
- •3. Қисық доғасының ұзындығы
1.Матрицаның
анықтамасы? Матрица
деп,
m- жол және n- бағаннан тұратын сандар
немесе әріптерден құрылған тік бұрышты
кестені айтады. Матрица латынның үлкен
әріптерімен белгіленеді A,B,C,…
және былай жазылады: немесе
қысқаша
немесе
қысқаша
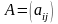 ,
мұндағы
,
мұндағы
 (яғни
(яғни
![]() )
– жолдың нөмірі,
)
– жолдың нөмірі,
![]() (яғни
(яғни
![]() )
– бағанның нөмірі.
)
– бағанның нөмірі.
А
матрицасын
![]() өлшемді матрица дейді және оны
өлшемді матрица дейді және оны
![]() деп жазады. Матрицаны құрайтын
деп жазады. Матрицаны құрайтын
![]() сандарын сол матрицаның элементтері
дейді.
сандарын сол матрицаның элементтері
дейді.
![]() элементтері бас диагоналді құрайды.
элементтері бас диагоналді құрайды.![]() -
-
![]() -
өлшемді матрица.
2.
Жол матрица дегеніміз не?
Бір ғана жатық жолдан құралған матрицаны
жол-матрица, ал бір ғана тік жолдан
құралған матрицаны бағана-матрица деп
атайды:
-
өлшемді матрица.
2.
Жол матрица дегеніміз не?
Бір ғана жатық жолдан құралған матрицаны
жол-матрица, ал бір ғана тік жолдан
құралған матрицаны бағана-матрица деп
атайды:
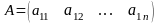 - жол-матрица;
- жол-матрица;
3.Баған
матрица?
 -
бағана матрица.
-
бағана матрица.
Бір
бағаннан тұратын матрицаны баған-матрица
дейді.
4.Квадрат
матрица?
Егер матрицаның жолдарының саны
бағандарының санына тең болса, ондай
матрицаны квадрат
матрица
дейді.
Оның өлшемі
![]() болады.
болады.
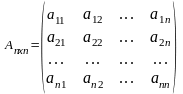 .
.
Квадрат
матрицаның
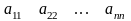 элементтері диагоналдық элементтер
деп аталады да, матрицаның негізгі
диагоналін құрайды. Ал
элементтері диагоналдық элементтер
деп аталады да, матрицаның негізгі
диагоналін құрайды. Ал
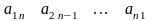 элементтері қосымша диагоналдық
элементтер деп аталады да, матрицаның
қосымша диагоналін құрайды.
элементтері қосымша диагоналдық
элементтер деп аталады да, матрицаның
қосымша диагоналін құрайды.
 5.Диагональ
матрица?
Егер квадрат матрицаның бас диагональдан
тыс элементтері нөлге тең болса, онда
ондай матрицаны диагональ
матрица
дейді.
5.Диагональ
матрица?
Егер квадрат матрицаның бас диагональдан
тыс элементтері нөлге тең болса, онда
ондай матрицаны диагональ
матрица
дейді.
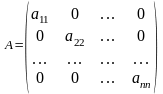 .
.
6.Бірлік матрица? Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,
 .
Барлық элементтері нолге тең матрица
нолдік матрица деп аталады.
.
Барлық элементтері нолге тең матрица
нолдік матрица деп аталады.
7.Үшбұрышты матрица дегеніміз не? Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,
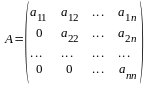 ,
,
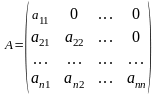
8.Матрицаларға қолданылатын амалдар? Матрицаны санға көбейту. 1. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
Мысалы,
 матрицасын
матрицасын
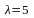 санына көбейтейік: .
санына көбейтейік: .
Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
2.Матрицаларды
қосу және алу.
2.
Матрицаларды қосу және алу.
Өлшемдері бірдей матрицаларды ғана
қосуға болады.
А және В матрицаларының қосындысы деп
элементтері осы матрицалардың сәйкес
элементтерінің қосындысы болатын, А +
В матрицаны айтамыз: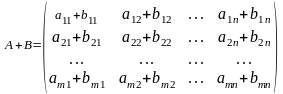 .
.
А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті: A – B = A+(-1)B немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады. Мысалы А матрицасынан В матрицасын алайық:
3.Матрицаларды көбейту. 3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі mxk болатын А матрицасы мен өлшемі kxn болатын В матриасы берілсін:
Осы екі матрицаны көбейткенде өлшемі mxn болатын көбейтінді С матрица аламыз:

С
матрицасының
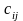 элементі А
матрицаның
элементі А
матрицаның
 –жатық
жол элементтерін В
матрицаның
–жатық
жол элементтерін В
матрицаның
 –тік
жолының сәйкес элементтеріне көбейтіп
қосқанға тең болады:
–тік
жолының сәйкес элементтеріне көбейтіп
қосқанға тең болады:
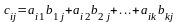 ,
,
 .
(1) Мысалы,
.
(1) Мысалы,
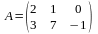 матрицасы мен
матрицасы мен
 матрицасын көбейтейік. Бірінші матрица
үш тік жолдан, ал екінші матрица үш
жатық жолдан тұрғандықтан бұл матрицаларды
көбейтуге болады. Көбейтінді матрицаның
өлшемін анықтайық:
матрицасын көбейтейік. Бірінші матрица
үш тік жолдан, ал екінші матрица үш
жатық жолдан тұрғандықтан бұл матрицаларды
көбейтуге болады. Көбейтінді матрицаның
өлшемін анықтайық:
 ,
яғни,
,
яғни,
 .
k=3
болғандықтан (1) формуланы қолданғанда
үш қосылғыш болады:
.
k=3
болғандықтан (1) формуланы қолданғанда
үш қосылғыш болады:
 ,
,
 .
.
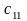 элементін табу үшін формуладағы i=1,
j=1 деп
аламыз, сонда
элементін табу үшін формуладағы i=1,
j=1 деп
аламыз, сонда
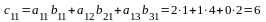 ,
яғни А
матрицаның 1-жатық жол элементтерін В
матрицаның 1-тік жолының сәйкес
элементтеріне көбейтіп қостық. Осылай
С матрицаның барлық элементтері
табылады:
,
яғни А
матрицаның 1-жатық жол элементтерін В
матрицаның 1-тік жолының сәйкес
элементтеріне көбейтіп қостық. Осылай
С матрицаның барлық элементтері
табылады:
C=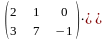
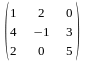 =
=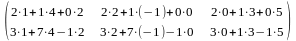 =
=
=
= .
.
Қосу және көбейту амалдарының мынадай қасиеттері бар:
1) A+B=B+A |
5) (A+B)C=AC+BC |
2) (A+B)+C=A+(B+C) |
6)
|
3) (A+B)= A+ B |
7) A(BC)=(AB)C |
4) A(B+C)=AB+AC |
|
|
|
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық.
8)
Біріншіден, екі матрицаның АВ
көбейтіндісі болғанмен ВА
көбейтіндісі болмауы мүмкін. Мысалы,
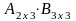 көбейтіндісі бар, бірақ
көбейтіндісі бар, бірақ
 көбейтіндісі жоқ, себебі бірінші
матрицаның тік жолдар саны екінші
матрицаның жатық жолдар санына тең
емес;
көбейтіндісі жоқ, себебі бірінші
матрицаның тік жолдар саны екінші
матрицаның жатық жолдар санына тең
емес;
екіншіден,
АВ
және ВА
көбейтінділері бар болғанмен, олардың
өлшемдері әртүрлі болуы мүмкін. Мысалы,
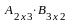 және
және
 көбейтінділер бар, бірақ өлшемдері
әртүрлі:
көбейтінділер бар, бірақ өлшемдері
әртүрлі:
 ,
,
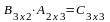 ;
үшіншіден, АВ
және ВА
көбетінділер бар және олардың өлшемдері
бірдей болғанмен, жалпы жағыдайда,
көбейтудің коммутативті заңы орындалмайды,
яғни АВ
;
үшіншіден, АВ
және ВА
көбетінділер бар және олардың өлшемдері
бірдей болғанмен, жалпы жағыдайда,
көбейтудің коммутативті заңы орындалмайды,
яғни АВ BA.
BA.
Мыс:
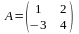 мен
мен
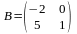 матрицалары берілген. АВ
және ВА
көбейтінділерін табау керек. Шешуі.
Берілген матрицалар өлшемдері 2х2
квадрат матрицалар, оларды көбейтуге
болады:
матрицалары берілген. АВ
және ВА
көбейтінділерін табау керек. Шешуі.
Берілген матрицалар өлшемдері 2х2
квадрат матрицалар, оларды көбейтуге
болады:
 .
.
 .
.
Көріп отырғанымыздай АВ BA.
9) А-квадрат матрица болса, онда мына теңдік орындалады: АЕ = ЕА = А.
9.Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері? Өлшемдері бірдей матрицаларды ғана қосуға болады. А және В матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз:
Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
Мысалы, матрицасын санына көбейтейік:Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
1. Матрицалардың санға көбейтіндісі.
Әрбір матрицаны санға көбейтуге болады. Ол үшін матрицаның әр элементін сол санға көбейту керек.
Мысалы ![]()
10. Матрицаларды көбейту амалының қасиеттері? Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі mxk болатын А матрицасы мен өлшемі kxn болатын В матриасы берілсін: Осы екі матрицаны көбейткенде өлшемі mxn болатын көбейтінді С матрица аламыз:
С матрицасының элементі А матрицаның –жатық жол элементтерін В матрицаның –тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады: , . (1) Мыс: матрицасы мен матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші матрица үш жатық жолдан тұрғандықтан бұл матрицаларды көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:
, яғни, . k=3 болғандықтан (1) формуланы қолданғанда үш қосылғыш болады: , . элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда , яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік жолының сәйкес элементтеріне көбейтіп қостық. Осылай С матрицаның барлық элементтері табылады:
C= = = = .
Қосу және көбейту амалдарының мынадай қасиеттері бар:
1) A+B=B+A |
5) (A+B)C=AC+BC |
2) (A+B)+C=A+(B+C) |
6) (AB)=( A)B=A( B) |
3) (A+B)= A+ B |
7) A(BC)=(AB)C |
4) A(B+C)=AB+AC |
|
|
|
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық8) Біріншіден, екі матрицаның АВ көбейтіндісі болғанмен ВА көбейтіндісі болмауы мүмкін. Мысалы, көбейтіндісі бар, бірақ көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес;
екіншіден, АВ және ВА көбейтінділері бар болғанмен, олардың өлшемдері әртүрлі болуы мүмкін. Мысалы, және көбейтінділер бар, бірақ өлшемдері әртүрлі: , ; үшіншіден, АВ және ВА көбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ BA.
Мыс: мен матрицалары берілген. АВ және ВА көбейтінділерін табау керек. Шешуі. Берілген матрицалар өлшемдері 2х2 квадрат матрицалар, оларды көбейтуге болады:
.
.Көріп отырғанымыздай АВ BA.
9) А-квадрат матрица болса, онда мына теңдік орындалады: АЕ = ЕА = А.
11.
Екінші ретті анақтауыштың анықтамасы
және есептелінілуі?
Екінші
ретті матрицаның
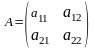 анықтауышы немесе екінші ретті анықтауыш
деп мынадай санды айтады:
анықтауышы немесе екінші ретті анықтауыш
деп мынадай санды айтады: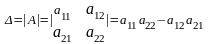
12. Үшінші ретті анақтауыштың анықтамасы және есептелінілуі? а матрицасының анықтауышы немесе 3-ші ретті анықтауышы деп, төменгі формуламен есептелінетін санды айтады:
![]()
![]()
![]() .
.
Үшінші ретті квадрат-матрицаға сәйкесті үшінші ретті анықтауыш деп
.
санын атап, мына символ арқылы белгілейді: Сонымен анықтама бойынша:
.
-формуламен анықталған үшінші ретті анықтауыш, оның мүшелері деп аталатын 3!=6 қосылғыштың алгебралық қосындысы болып табылады. Анықтауыштың әрбір мүшіесі оң немес теріс таңбаларымен алынған және сәйкес үш ретті квадрат матрицаның әрбір жатық жолы әрбір тік жолдарында бір-бірден орналасқан үш элементтер көбейтіндісі болып табылады. Енді анықтауыш мүшелерін құрудың мынадай қарапайым ережесін келтірейік. Бірінші мүшесі анықтауыштың бас диагоналінің бойында жаткан элементтерінің көбейтіндісі болады. Екінші және үшінші мүшелері- бас диагоналге параллельдің бойында жаткан екі элемент пен анықтауыштың қарама-қарсы бұрышында жатқан үшінші элементінің көбейтіндісіне тең.
Анықтауыштың бұл үш мүшесі оң таңбамен алынады(а). Осылайша анықтауыштың теріс таңбалы мүшелері құралады. Мұнда анықтауыштың бас диагоналінің орнына жанама диагоналі алынады (б). Бұл ереже үшбұрыш ережесі деп аталады.
Үшінші
ретті анықтауыштың қасиеттері.
1. Анықтауштың жатық жолдарын оның
сәйкес тік жолдарымен орын алмастырғаннан
ол анықтауыштың сан мәні өзгермейді.
Анықтауыштың жатық жолдары мен тік
жолдарының орын алмастыру амалы оны
транспозициялау деп аталады.
2. Егер
анықтауыштың қандай болса да бір жатық
жолының барлық элементтері нөлге тең
болса, онда анықтауышнөлге тең болады.
3.
Егер анықтауыштың екі жатық жолын бірі
мен бірін орныдарынан алмастырсақ,
онда анықтауыш таңбасы қарама-қарсы
таңбаға ауады.
4. Егер анықтауыштың кез келген екі
жатық жолы өзара тең болса, онда ол
нөлге тең болады.
5. Егер анықтауыштың
қандай болса да бір жатық жолының барлық
элементтерін бір ғана
 санына көбейтсек, онда анықтауыштың
өзі осы γ санына көбетіледі.
6. Егер
анықтауыштың екі жатық жолының
элементтері пропорционал болса, онда
мұндай анықтауыш нөлге тең болады.
Егер анықтауыштың
і-ші жатық
жолының элементтері екі қосылғыш арқылы
берілген болса, яғни
санына көбейтсек, онда анықтауыштың
өзі осы γ санына көбетіледі.
6. Егер
анықтауыштың екі жатық жолының
элементтері пропорционал болса, онда
мұндай анықтауыш нөлге тең болады.
Егер анықтауыштың
і-ші жатық
жолының элементтері екі қосылғыш арқылы
берілген болса, яғни
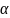 іj
=
іj
= іj
+
іj
+
 ,
ij=1,2,3 онда
анықтауыш екі анықтауыштың қосындысына
тең болады. Егер анықтауыштың қандай
болса да бір жатық жолының элементтерін
бір ғана
санына
көбейтіп, басқа бір жатық жолының сәйкес
элементтеріне қоссақ, онда бұдан
анықтауыш шамасы өзгермейді.
13.
Элементінің
миноры дегеніміз не? 4)
,
ij=1,2,3 онда
анықтауыш екі анықтауыштың қосындысына
тең болады. Егер анықтауыштың қандай
болса да бір жатық жолының элементтерін
бір ғана
санына
көбейтіп, басқа бір жатық жолының сәйкес
элементтеріне қоссақ, онда бұдан
анықтауыш шамасы өзгермейді.
13.
Элементінің
миноры дегеніміз не? 4)
![]() квадрат
матрицасының
элементінің
миноры
деп, осы элемент орналасқан жол мен
бағанды сызып тастағаннан шығатын 3-ші
ретті анықтауышты айтады және оны
квадрат
матрицасының
элементінің
миноры
деп, осы элемент орналасқан жол мен
бағанды сызып тастағаннан шығатын 3-ші
ретті анықтауышты айтады және оны
![]() деп белгілейді.
14.
Элементінің алгебралық толықтауышы
дегеніміз не?
Ал
деп белгілейді.
14.
Элементінің алгебралық толықтауышы
дегеніміз не?
Ал
![]() саны
элементінің
алгебралық
толықтауышы
деп аталады.
15.Анықтауыштың
қасиеттері?
Анықтауыш
Қасиеттері
саны
элементінің
алгебралық
толықтауышы
деп аталады.
15.Анықтауыштың
қасиеттері?
Анықтауыш
Қасиеттері
1-қасиет. Анықтауыштың жатық жолдарын сәкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен, анықтауыш мәні өзгермейді:
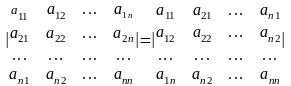 .
.
Теңдіктің дұрыстығын анықтауыштарды есептеу арқылы тексеруге болады.
2-қасиет. Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. Үшінші ретті анықтауыштың екінші жолындағы ортақ көбейткішті анықтауыш алдына шығарамыз:

 .
.
Теңдіктің дұрыстығына берілген матрицаны екінші жол бойынша жіктеп тексеруге болады.
3-қасиет. Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. Үшінші ретті анықтауыштың бірінші және екінші жолдарын алмастырайық:
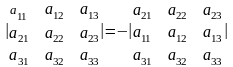
Теңдіктің дұрыстығын екінші анықтауышты бірінші жол бойынша жіктеп тексеруге болады.
4-қасиет. Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нолге тең. Үшінші ретті анықтауыштың бірінші және екінші жолдары бірдей болсын:
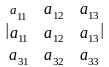 =0.
=0.
Теңдіктің дұрыстығын осы екі жолдың орндарын алмастырып 3-қасиетті қолданып тек. болады.
5-қасиет. Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді. Үшінші ретті анықтауыштың бірінші жолын -ға көбейтіп екінші жолға қосайық:
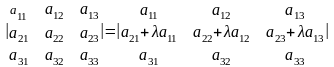 .
.
Теңдіктің дүрыстығын екінші анықтауышты мынадай
+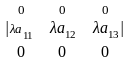
анықтауыштардың қосындысы түрінде жазайық. Сонда бірінші қосылғыш берілген анықтауыш болады да, екінші анықтауыш нолге тең.
6-қасиет. Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісіне тең:
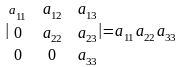 .
.
Теңдіктің дұрыстығын анықтауышты бірінші тік немесе үшінші жатық жол бойынша жіктеп тексеруге болады.
Осы қасиеттер көмегімен жоғары ретті анықтауыштар есептеуді көп жеңілдетуге болады. Анықтауышты қандай да бір жолында неғұрлым көп ноль болатындай етіп түрлендіріп, сол жол бойынша жіктеп анықтауыш реті төмендетіледі. Мысалы мынадай төртінші ретті
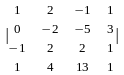 анықтауышты
есептейік.
анықтауышты
есептейік.
Анықтауышты
үшбұрышты түрге келтіреміз. Алдымен
5-қасиет бойынша анықтауыштың бірінші
жолын 1-ге көбейтіп үшінші жолға, (-1)-ге
көбейтіп төртінші жолға қосайық (есепте
көрсетілген). Сонда анықтауыштың бірінші
тік жолында
 элементтен басқасы нолге айналады.
элементтен басқасы нолге айналады.
Енді
осы қасиетті пайдаланып
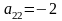 элементінің астында тұрған сандарды
нолге айналдырамыз. Соңында
элементінің астында тұрған сандарды
нолге айналдырамыз. Соңында
 элементінің астында тұрған сандарды
нолге айналдырамыз. Анықтауыш үшбұрышты
түрге келді. 6-қасиет бойынша анықтауыш
мәнін диагональдік элементтерді
көбейтіп табамыз.
элементінің астында тұрған сандарды
нолге айналдырамыз. Анықтауыш үшбұрышты
түрге келді. 6-қасиет бойынша анықтауыш
мәнін диагональдік элементтерді
көбейтіп табамыз.
 =
=
 =
=

 =
=
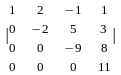 =
= .
.
Анықтауыштың қасиеттері:
1. Анықтауыштың жолдарын сәйкес бағандармен алмастырғаннан анықтауыштың мәні өзгермейді.
2. Егер анықтауыштың қандай да бір жолы (бағаны) тек нөлден тұрса, онда анықтауыш нөлге тең.
3.Егер анықтауыштың екі жолы (бағаны) пропорционал болса, онда анықтауыш нөлге тең.
4. Жолдың (бағанның) ортақ көбейткішін анықтауыштың алдына шығарып жазуға болады.
5.Егер анықтауыштың екі жолын (бағанын) алмастырса, онда анықтауыштың таңбасы өзгереді.
6. Егер қандай да бір жолдың (бағанның) элементтеріне кез келген санға көбейтілген басқа жолдың сәйкес элементтерін қосқаннан анықтауыш өзгермейді. 16. Матрицаның рангі? Матрицанің рангісі
mxn
өлшемді А матрицаның бірнеше жатық
және тік жолдарын сызып тастап k
өлшеміді,
k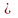 min(m,n),
квадрат матрица алуға болады. Осы
квадрат матрица анықтауышы берілген
матрицаның k өлшемді миноры деп аталады.
min(m,n),
квадрат матрица алуға болады. Осы
квадрат матрица анықтауышы берілген
матрицаның k өлшемді миноры деп аталады.
 матрицаның
k-өлшемді
минорлар саны
матрицаның
k-өлшемді
минорлар саны
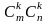 болады. Анықтама. Матрицаның
нолге тең емес минорларының ең үлкен
реті матрица
рангісі
деп аталады:
r=r(A)=
rangA
.
болады. Анықтама. Матрицаның
нолге тең емес минорларының ең үлкен
реті матрица
рангісі
деп аталады:
r=r(A)=
rangA
.
1. матрицасының рангісі оның өлшемдерінің кішісінен артпайды: r(A) min(m,n).
2. Барлық элементтері ноль болғанда ғана (нолдік матрица) матрица рангісі ноль болады.
3. n–ретті квадрат матрица ерекше емес болғанда матрица рангісі n–ге тең болады.
Мысал.
 матрицаның рангісін есептейік.
матрицаның рангісін есептейік.
Шешуі. Матрица өлшемі 3х4 болғандықтан, оның рангісі 3-тен артпайды, r(A) min(3,4). Егер үшінші ретті минорлардың ең болмағанда біреуі нолден өзгеше болса, онда матрица рангісі 3-ке тең болады. Үшінші ретті минорлар матрицаның бір тік жолын сызып тастағанда пайда болады:
 ,
,
 ,
,
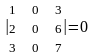 ,
,
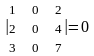 .
.
Үшінші
ретті минорлардың бәрі нолге тең
болғандықтан, ранг 3-ке тең бола алмайды.
Енді екінші ретті минорлардың ішінен
(олардың саны
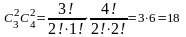 )
ең болмағанда бір нолге тең емес минор
тапсақ, матрица рангісі 2-ге тең болады.
Екінші ретті минорлар матрицаның бір
жатық, екі тік жолын сызып тастағанда
пайда болады. Айталық бірінші жатық
жол мен бірінші және екінші тік жолдарды
сызып тастағанда пайда болатын мына
минор:
)
ең болмағанда бір нолге тең емес минор
тапсақ, матрица рангісі 2-ге тең болады.
Екінші ретті минорлар матрицаның бір
жатық, екі тік жолын сызып тастағанда
пайда болады. Айталық бірінші жатық
жол мен бірінші және екінші тік жолдарды
сызып тастағанда пайда болатын мына
минор:
 ,
сондықтан r(A)=2.
,
сондықтан r(A)=2.
Матрица өлшемі артқан сайын оның рангісін барлық нолден өзге минорларды есептеу жолымен анықтау қиындайды. Матрица рангісін элементар түрлендірулер әдісімен табу ондай қиындықтардан құтқарады.
Теорема. Элементар түрлендірулер матрица рангісін өзгертпейді.
Дәлелдеуі. Матрицаға элементар түрлендірулер жүргізгенде оның анықтауышы не өзгермей сақталады, не нолге тең емес санға көбейтіледі. Яғни, оның реті өзгермейді деген сөз. Олай болса, нолден өзгеше минорлардың немесе матрица рангісінің реті де өзгермейді.
Осы
теореманы ескеріп, элементар түрлендірулер
жасап, берілген матрицаны барлық
диагоналдік элементтері нолден өзгеше
болатындай етіп сатылы түрге келтіреміз: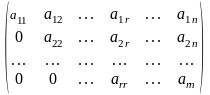 ,
,
мұндағы r п. Осы шарттың орындалуын матрицаны транстонерлеу арқылы қамтамасыз етуге болады. Сонда матрицаның r–ретті нолден өзге миноры
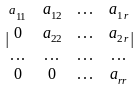 бар
болады да, матрица рангісі r-ге
тең болады, яғни r(A)=r.
бар
болады да, матрица рангісі r-ге
тең болады, яғни r(A)=r.
Матрицаның рангы деп
нольге тең емес минордың ең жоғарғы
ретін айтады. Матрицаның рангі өзгермейді
матрицасының
рангiн табайық.
Шешуi.
![]() бесінші
жолдың элементтерiн 2-ге бөлейiк:
~
бесінші
жолдың элементтерiн 2-ге бөлейiк:
~ ![]() бірінші
жолдың элементтерiн бесінші жолдың
сәйкес элементтерiне қосамыз:
~
бірінші
жолдың элементтерiн бесінші жолдың
сәйкес элементтерiне қосамыз:
~ ![]() екінші
жолдың элементтерiн 2-ге көбейтiп,
төртінші жолдан аламыз:
~
екінші
жолдың элементтерiн 2-ге көбейтiп,
төртінші жолдан аламыз:
~ ![]() ~
бірінші
жолды төртінші жолға қосамыз:
~
~
бірінші
жолды төртінші жолға қосамыз:
~ ![]() ~
үшінші
жолдан екінші жолды аламыз:
~
~
үшінші
жолдан екінші жолды аламыз:
~ ![]() ~
үшінші
жолдан бірінші жолды аламыз:
~
~
үшінші
жолдан бірінші жолды аламыз:
~ ![]() ~
~ ![]() Бұл
матрицаның рангi r=2, себебi:
Бұл
матрицаның рангi r=2, себебi:
![]() Демек
берiлген матрицаның рангi 2-ге тең болады
екен.
Матрицаның
рангiн табуға мына теореманы пайдаланған
жөн болады.
Егер
mxn өлшемдi матрицаның элементтерiнен
жасалған r реттi бiр миноры нөлге тең
емес, ал ол минордың ретiн бiрге арттырудан
шығатын минордың (яғни жиектелiп шыққан
минорлар) барлығы нөл болса, онда
берiлген матрицаның рангi r-ге тең
болады.
17.
Матрицаны түрлендіру?
18.Кері
матрица? Кері
матрицаның анықтамасы
Демек
берiлген матрицаның рангi 2-ге тең болады
екен.
Матрицаның
рангiн табуға мына теореманы пайдаланған
жөн болады.
Егер
mxn өлшемдi матрицаның элементтерiнен
жасалған r реттi бiр миноры нөлге тең
емес, ал ол минордың ретiн бiрге арттырудан
шығатын минордың (яғни жиектелiп шыққан
минорлар) барлығы нөл болса, онда
берiлген матрицаның рангi r-ге тең
болады.
17.
Матрицаны түрлендіру?
18.Кері
матрица? Кері
матрицаның анықтамасы
Кез
келген
 сан үшін мына
сан үшін мына
 теңдігін қанағаттандыратындай кері
сан табылады. Квадрат матрица үшін де
осындай ұғым енгіземіз. Анықтама.
А
квадрат
матрица үшін мына
теңдігін қанағаттандыратындай кері
сан табылады. Квадрат матрица үшін де
осындай ұғым енгіземіз. Анықтама.
А
квадрат
матрица үшін мына
 теңдікті
қанағаттандыратын
теңдікті
қанағаттандыратын
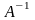 матрица А
матрицаның
кері матрицасы деп
аталады.
Кері
матрицаны мына формуламен табады:
матрица А
матрицаның
кері матрицасы деп
аталады.
Кері
матрицаны мына формуламен табады:
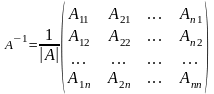 ,
мұндағы
,
мұндағы
 -матрица
анықтауышы, ал
-матрица
анықтауышы, ал
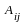 -берілген
матрицаның
-берілген
матрицаның
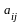 элементтерінің алгебралық толықтауыштары,
i=1,2,…,n;
j=1,2,…,n.
элементтерінің алгебралық толықтауыштары,
i=1,2,…,n;
j=1,2,…,n.
Кез
келген квадрат матрицаның кері матрицасы
бола бермейді. Теорема(кері
матрица болуының қажетті және жеткілікті
шарты). Матрицаның
кері матрицасы болуы үшін ол ерекше
емес ( )
матрица болуы қажетті және жеткілікті.
)
матрица болуы қажетті және жеткілікті.
Мысал.
 матрицасының кері матрицасын табу
керек. Шешуі.
Алдымен анықтауышын есептейік.
матрицасының кері матрицасын табу
керек. Шешуі.
Алдымен анықтауышын есептейік.
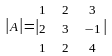
 =
=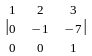 =
=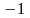 .
.
 ,
яғни кері матрица бар. Енді элементтердің
алгебралық толықтауыштарын есептейік.
,
яғни кері матрица бар. Енді элементтердің
алгебралық толықтауыштарын есептейік.
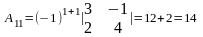 ,
,
 ,
,
 ,
,
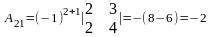 ,
,
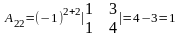 ,
,
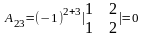 ,
,
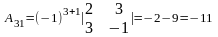 ,
,
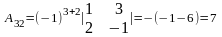 ,
,
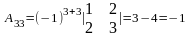 .
.
Табылған мәндерді формулаға қойып кері матрицаны табамыз.
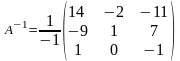
 .
Кері матрицаның дұрыс табылғандығын
.
Кері матрицаның дұрыс табылғандығын
 теңдігін тексеру арқылы көз жеткізуге
болады:
теңдігін тексеру арқылы көз жеткізуге
болады:
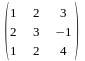

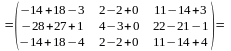
 19. Жүйенің шешімі дегеніміз
не?
19. Жүйенің шешімі дегеніміз
не?

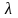 (AB)=(
A)B=A(
B)
(AB)=(
A)B=A(
B)