- •2 Негізгі таратылатын материалдар мазмұны
- •2.1 Курстың тақырыптық жоспары
- •1Бөлім Механика
- •1 Кинематика
- •Материялық нүкте қозғалысының кинематикалық сипаттамалары
- •1.2 Траектория, жол ұзындығы, орын ауыстыру векторы
- •1.3 Жылдамдық
- •1.4 Үдеу және оның құраушылары
- •1.5 Қатты дененің ілгерілмелі қозғалысы
- •1.6 Айналмалы қозғалыс кинематикасы
- •Қатты дененің ілгерілмелі қозғалысының және материялық нүктенің динамикасы
- •2.1 Ньютонның бірінші заңы – инерция заңы
- •2.2 Күш. Масса
- •2.3 Ньютонның екінші заңы– материялық нүкте динамикасының негізгі заңы
- •2.4 Ньютонның үшінші заңы
- •2.5 Қатты дененің ілгерілмелі қозғалыс динамикасының негізгі заңы
- •2.6 Импульстің сақталу заңы
- •2.7 Механикалық жүйенің массалар центрі және оның қозғалыс заңдары
- •2.8 Механикадағы күш түрлері
- •2.9 Энергия, күш жұмысы, қуат
- •2.10 Денелер жүйесінің механикалық энергиясы
- •2.11 Механикалық энергияның сақталу заңы
- •3 Қатты дененің айналмалы қозғалыс динамикасы
- •3.1 Күш моменті
- •3.2 Дененің инерция моменті
- •4.1 Айналмалы қозғалыстағы дененің жұмысы және кинетикалық энергиясы
- •4.2 Қатты дененің айналмалы қозғалыс динамикасының негізгі теңдеуі
- •4.3 Импульс моменті және оның сақталу заңы
- •4.3 Импульс моментінің сақталу заңын дәлелдеу
- •Арнайы салыстырмалы теорияның элементтері
- •Релятивистік динамика элементтері
- •5 Тұтас орта механикасының элементтері
- •5.1 Ағынның үздіксіздік теңдеуі
- •5.2 Бернулли теңдеуі
- •5.2.1 Сұйықтықтың горизонталь ағуы
- •5.2.2 Сұйықтықтың тесіктен ағуы
- •5.3 Тұтқырлық
- •5.4 Сұйық ағынының екі түрі
- •Тербелістер мен толқындар
- •6.1 Механикалық гармониялық тербелістер және олардың сипаттамалары
- •6.2 Гармониялық тербелістегі материялық нүкте энергиясы
- •6.3 Гармониялық осцилляторлар
- •6.3 Өшетін тербелістер
- •6.4 Еріксіз тербелістер
- •6.5 Механикалық гармониялық толқындар
- •6.6 Жазық қума толқынның теңдеуі
- •6.7 Тұрғын толқындар
- •II бөлім . Молекулалық физика және термодинамика
- •7 Термодинамикалық жүйелер мен олардың параметрлері
- •7.1 Термодинамикалық параметрлер мен процестер
- •7.2 Идеал газдың күй теңдеуі
- •7.3 Идеал газдардың молекула-кинетикалық теориясы
- •7.4 Газ молекулаларының ілгерілемелі қозғалысының орташа кинетикалық энергиясы
- •7.5 Статистикалық таралу
- •7.5.1 Энергияның еркіндік дәрежелер бойынша бірқалыпты таралу заңы
- •7.5.2 Сыртқы күш өрісіндегі бөлшектер үшін Больцман таралуы
- •7.5.3 Газ молекулаларының жылдамдықтар бойынша таралу заңы (Максвелл заңы)
- •7.6 Термодинамикалық тепе-теңдіксіз жүйелердегі тасымалдау құбылыстары
- •7.6.1 Диффузия
- •7.6.2 Ішкі кедергі
- •Термодинамикның бірінші бастамасы
- •8.1 Жүйенің ішкі энергиясы
- •8.2 Жұмыс және жылу
- •8 Термодинамиканың бірінші заңы
- •8.4 Термодинамикалық процестер мен жұмыстың графиктері
- •8.5 Заттың жылусыйымдылығы
- •8.6 Термодинамиканың бірінші бастамасын идеал газдардағы изопроцестерге қолдану
- •8.6.1 Изохоралық процесс ( )
- •8.6.2 Изобаралық процесс ( )
- •8.6.3 Изотермиялық процесс ( )
- •8.6.4 Адиабаталық процесс ( )
- •8.6.5 Политроптық процесс ( )
- •Термодинамиканың екінші бастамасы
- •9.1 Қайтымды және қайтымсыз процестер
- •9.2 Дөңгелек процестер
- •9.3 Карноның идеал жылулық машинасы
- •9.4 Карно теоремасы
- •9.5 Клаузиус теңсіздігі
- •9.6 Энтропия
- •9.6.1 Энтропияның қасиеттері
- •9.7 Термодинамиканың екінші бастамасы
- •Нақты газдар мен булар
- •10.1 Молекула көлемін ескеру
- •10.2 Молекулалардың тартылыс күшін ескеру
- •10.4 Заттың критикалық күйі. Фазалық ауысулар
- •– Газдың универсал тұрақтысы. Сонымен, Ван-дер-Ваальс теңдеуі газ күйін, газдың сұйықтыққа айналу процесін және сұйықтықтың сығылуын сипаттай алады.
- •10.5 Нақты газдың ішкі энергиясы
- •III бөлім. Электр өрісі
- •Кулон заңы
- •Электрстатикалық өріс кернеулігі
- •Гаусс теоремасы
- •Электрстатикалық өрістердің қасиеттері
- •Электр өрісіндегі өткізгіштер
- •Электрлік сыйымдылық. Оқшауланған өткізгіштің электрлік сыйымдылығы
- •Өзара сыйымдылық. Конденсаторлар.
- •Электрстатикалық өрістегі диэлектриктер. Диэлектриктердің түрлері.
- •Диэлектриктердің поляризациясы. Поляризациялану.
- •Поляризациялық зарядтар
- •Электрлік ығысу векторы
- •Электр зарядтарының энергиясы
- •Зарядталған конденсатордың энергиясы
- •Өзара әсерлесуші зарядтардың энергиясы
- •Зарядталған өткізгіштің энергиясы
- •Ток күші және ток тығыздығы
- •Тармақталған тізбектерге арналған Кирхгоф ережелері
- •Газдардың электрөткізгіштігі
10.1 Молекула көлемін ескеру
Бөлшектер қатты жақындағанда олардың тебу күштері арта бастайды. Молекулалар бір-біріне кеңістіктегі алып тұрған орындарынан жақын орналаса алмайды. Сондықтан, газдың көлемі молекулалардың санына пропорционал b шамаға кем болу керек. Бір моль газдың көлемі келесі шамаға тең болады:
(![]() ).
(10.1)
).
(10.1)
Шар
тәрізді молекулаларды барынша тығыз
орналастырса да, олардың арасында
қуыстар қалады. Олай болса,
![]() тұрақтысы бір моль газдағы барлық
молекулалардың көлемдерінің қосындысынан
әрқашан
артық
болады.
тұрақтысы бір моль газдағы барлық
молекулалардың көлемдерінің қосындысынан
әрқашан
артық
болады.
10.2 Молекулалардың тартылыс күшін ескеру
Молекуалардың
өзара тартылыс күші газ ішінде ішкі
қысым
деп аталатын қосымша қысым тудырады.
Сондықтан күй теңдеуіндегі р
қысымды (p+p1)
шамасымен ауыстыру керек. Ван-дер-Ваальстің
зерттеулері ішкі қысым молекулалар
концентрациясының квадратына тура,
мольдік көлем (![]() )
квадратына кері пропорционал болатынын
көрсетті:
)
квадратына кері пропорционал болатынын
көрсетті:
![]() ,
(10.2)
,
(10.2)
мұндағы а – газдың табиғатына тәуелді болатын тұрақты шама. Осы екі түзетуді Клапейрон теңдеуіне енгізсек, нақты газдың бір молі үшін күй теңдеуін аламыз (Ван-дер-Ваальс теңдеуі):
![]() .
(10.3)
.
(10.3)
Газдың
кез-келген мөлшеріне (![]() )
арналған күй теңдеуінің түрі:
)
арналған күй теңдеуінің түрі:
![]() ,
(10.4)
,
(10.4)
мұндағы
![]() мен
– эксперимент арқылы анықталатын
тұрақты шамалар;
мен
– эксперимент арқылы анықталатын
тұрақты шамалар;
![]() – газ алып тұрған көлем. Ван-дер-Ваальс
теңдеуін шығарарда бірқатар оңайлатулар
енгізілгендіктен, бұл теңдеу нақты газ
күйін жуықтап сипаттайды. Нақты газ
күйін сипаттайтын басқа да теңдеулер
бар. Бірақ олар күрделі болғандықтан
мұнда қарастырылмайды.
– газ алып тұрған көлем. Ван-дер-Ваальс
теңдеуін шығарарда бірқатар оңайлатулар
енгізілгендіктен, бұл теңдеу нақты газ
күйін жуықтап сипаттайды. Нақты газ
күйін сипаттайтын басқа да теңдеулер
бар. Бірақ олар күрделі болғандықтан
мұнда қарастырылмайды.
10.3 Ван-дер-Ваальс изотермаларын талдау
Ван-дер-Ваальс
теңдеуі
![]() көлем
бойынша үшінші дәрежелі теңдеу. Сондықтан
p қысым мен T температураның берілген
мәні үшін бұл теңдеудің үш түбірі болады.
Түбірлердің екеуі комплекстік болуы
мүмкін. Көлем нақты шама болғандықтан,
р мен Т – ның кез-келген берілген мәнінде
V бір немесе үш мәнге ие болуы мүмкін.
Ван-дер-Ваальс теңдеулерін
талдау үшін оның
көлем
бойынша үшінші дәрежелі теңдеу. Сондықтан
p қысым мен T температураның берілген
мәні үшін бұл теңдеудің үш түбірі болады.
Түбірлердің екеуі комплекстік болуы
мүмкін. Көлем нақты шама болғандықтан,
р мен Т – ның кез-келген берілген мәнінде
V бір немесе үш мәнге ие болуы мүмкін.
Ван-дер-Ваальс теңдеулерін
талдау үшін оның
![]() температуралар үшін
изотермаларын салайық
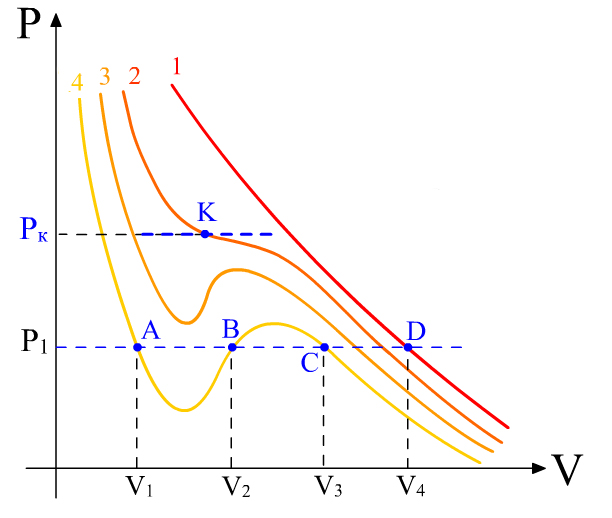
(10.1–cуреттегі 1,2,3,4 изотермалар).
Графиктерді зерттеу арқылы келесі үш
қорытынды жасауға болады:
температуралар үшін
изотермаларын салайық
(10.1–cуреттегі 1,2,3,4 изотермалар).
Графиктерді зерттеу арқылы келесі үш
қорытынды жасауға болады:
1.
Температура
( 2. Температуралар (Т2, Т3 және Т4) төмендеу болса, изотермаларда бүгілістер пайда болады. изобара мен 4 изотерма үш нүктеде (А,В,С) қиылысады. Бұл |
10.1 – cурет. Ван-дер-Ваальс изотермалары. |
нүктелер көлемнің р1 қысым мен Т4 температурадағы үш нақты мәндеріне (V1, V2, V3) сәйкес келеді.
3.
Температура өсіп 4 изотермадан 3 және 2
изотермаларға ауысқан сайын қисықтардағы
бүгіліс түзеле береді. А
және С
нүктелерінің ара қашықтығы азайып, 2
изотермада бір нүктеге – К
бүгіліс нүктесіне бірігіп кетеді. Бұл
нүктеден өтетін изобара
![]() изотермаға
жанама болады. Изотермасында бүгіліс
нүктесі бар Т2
температура
(сындық)
критикалық температура
деп аталады.
изотермаға
жанама болады. Изотермасында бүгіліс
нүктесі бар Т2
температура
(сындық)
критикалық температура
деп аталады.