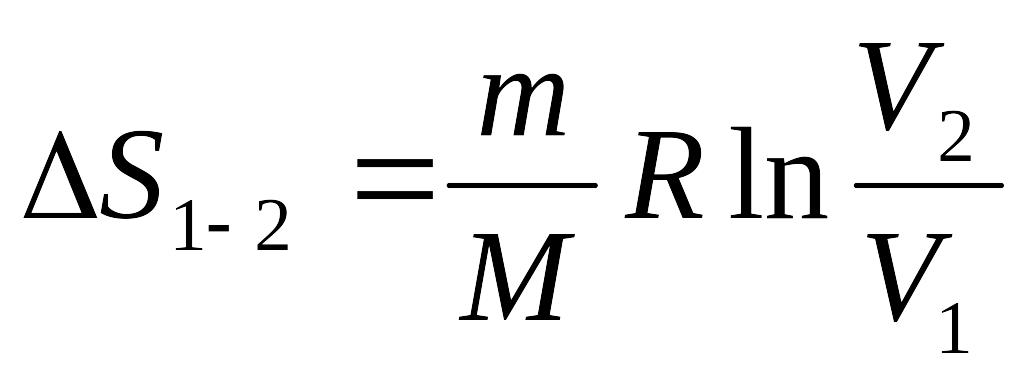- •2 Негізгі таратылатын материалдар мазмұны
- •2.1 Курстың тақырыптық жоспары
- •1Бөлім Механика
- •1 Кинематика
- •Материялық нүкте қозғалысының кинематикалық сипаттамалары
- •1.2 Траектория, жол ұзындығы, орын ауыстыру векторы
- •1.3 Жылдамдық
- •1.4 Үдеу және оның құраушылары
- •1.5 Қатты дененің ілгерілмелі қозғалысы
- •1.6 Айналмалы қозғалыс кинематикасы
- •Қатты дененің ілгерілмелі қозғалысының және материялық нүктенің динамикасы
- •2.1 Ньютонның бірінші заңы – инерция заңы
- •2.2 Күш. Масса
- •2.3 Ньютонның екінші заңы– материялық нүкте динамикасының негізгі заңы
- •2.4 Ньютонның үшінші заңы
- •2.5 Қатты дененің ілгерілмелі қозғалыс динамикасының негізгі заңы
- •2.6 Импульстің сақталу заңы
- •2.7 Механикалық жүйенің массалар центрі және оның қозғалыс заңдары
- •2.8 Механикадағы күш түрлері
- •2.9 Энергия, күш жұмысы, қуат
- •2.10 Денелер жүйесінің механикалық энергиясы
- •2.11 Механикалық энергияның сақталу заңы
- •3 Қатты дененің айналмалы қозғалыс динамикасы
- •3.1 Күш моменті
- •3.2 Дененің инерция моменті
- •4.1 Айналмалы қозғалыстағы дененің жұмысы және кинетикалық энергиясы
- •4.2 Қатты дененің айналмалы қозғалыс динамикасының негізгі теңдеуі
- •4.3 Импульс моменті және оның сақталу заңы
- •4.3 Импульс моментінің сақталу заңын дәлелдеу
- •Арнайы салыстырмалы теорияның элементтері
- •Релятивистік динамика элементтері
- •5 Тұтас орта механикасының элементтері
- •5.1 Ағынның үздіксіздік теңдеуі
- •5.2 Бернулли теңдеуі
- •5.2.1 Сұйықтықтың горизонталь ағуы
- •5.2.2 Сұйықтықтың тесіктен ағуы
- •5.3 Тұтқырлық
- •5.4 Сұйық ағынының екі түрі
- •Тербелістер мен толқындар
- •6.1 Механикалық гармониялық тербелістер және олардың сипаттамалары
- •6.2 Гармониялық тербелістегі материялық нүкте энергиясы
- •6.3 Гармониялық осцилляторлар
- •6.3 Өшетін тербелістер
- •6.4 Еріксіз тербелістер
- •6.5 Механикалық гармониялық толқындар
- •6.6 Жазық қума толқынның теңдеуі
- •6.7 Тұрғын толқындар
- •II бөлім . Молекулалық физика және термодинамика
- •7 Термодинамикалық жүйелер мен олардың параметрлері
- •7.1 Термодинамикалық параметрлер мен процестер
- •7.2 Идеал газдың күй теңдеуі
- •7.3 Идеал газдардың молекула-кинетикалық теориясы
- •7.4 Газ молекулаларының ілгерілемелі қозғалысының орташа кинетикалық энергиясы
- •7.5 Статистикалық таралу
- •7.5.1 Энергияның еркіндік дәрежелер бойынша бірқалыпты таралу заңы
- •7.5.2 Сыртқы күш өрісіндегі бөлшектер үшін Больцман таралуы
- •7.5.3 Газ молекулаларының жылдамдықтар бойынша таралу заңы (Максвелл заңы)
- •7.6 Термодинамикалық тепе-теңдіксіз жүйелердегі тасымалдау құбылыстары
- •7.6.1 Диффузия
- •7.6.2 Ішкі кедергі
- •Термодинамикның бірінші бастамасы
- •8.1 Жүйенің ішкі энергиясы
- •8.2 Жұмыс және жылу
- •8 Термодинамиканың бірінші заңы
- •8.4 Термодинамикалық процестер мен жұмыстың графиктері
- •8.5 Заттың жылусыйымдылығы
- •8.6 Термодинамиканың бірінші бастамасын идеал газдардағы изопроцестерге қолдану
- •8.6.1 Изохоралық процесс ( )
- •8.6.2 Изобаралық процесс ( )
- •8.6.3 Изотермиялық процесс ( )
- •8.6.4 Адиабаталық процесс ( )
- •8.6.5 Политроптық процесс ( )
- •Термодинамиканың екінші бастамасы
- •9.1 Қайтымды және қайтымсыз процестер
- •9.2 Дөңгелек процестер
- •9.3 Карноның идеал жылулық машинасы
- •9.4 Карно теоремасы
- •9.5 Клаузиус теңсіздігі
- •9.6 Энтропия
- •9.6.1 Энтропияның қасиеттері
- •9.7 Термодинамиканың екінші бастамасы
- •Нақты газдар мен булар
- •10.1 Молекула көлемін ескеру
- •10.2 Молекулалардың тартылыс күшін ескеру
- •10.4 Заттың критикалық күйі. Фазалық ауысулар
- •– Газдың универсал тұрақтысы. Сонымен, Ван-дер-Ваальс теңдеуі газ күйін, газдың сұйықтыққа айналу процесін және сұйықтықтың сығылуын сипаттай алады.
- •10.5 Нақты газдың ішкі энергиясы
- •III бөлім. Электр өрісі
- •Кулон заңы
- •Электрстатикалық өріс кернеулігі
- •Гаусс теоремасы
- •Электрстатикалық өрістердің қасиеттері
- •Электр өрісіндегі өткізгіштер
- •Электрлік сыйымдылық. Оқшауланған өткізгіштің электрлік сыйымдылығы
- •Өзара сыйымдылық. Конденсаторлар.
- •Электрстатикалық өрістегі диэлектриктер. Диэлектриктердің түрлері.
- •Диэлектриктердің поляризациясы. Поляризациялану.
- •Поляризациялық зарядтар
- •Электрлік ығысу векторы
- •Электр зарядтарының энергиясы
- •Зарядталған конденсатордың энергиясы
- •Өзара әсерлесуші зарядтардың энергиясы
- •Зарядталған өткізгіштің энергиясы
- •Ток күші және ток тығыздығы
- •Тармақталған тізбектерге арналған Кирхгоф ережелері
- •Газдардың электрөткізгіштігі
9.5 Клаузиус теңсіздігі
Карно теоремасына бойынша:
немесе ![]() .
.
Олай болса,
 немесе
немесе
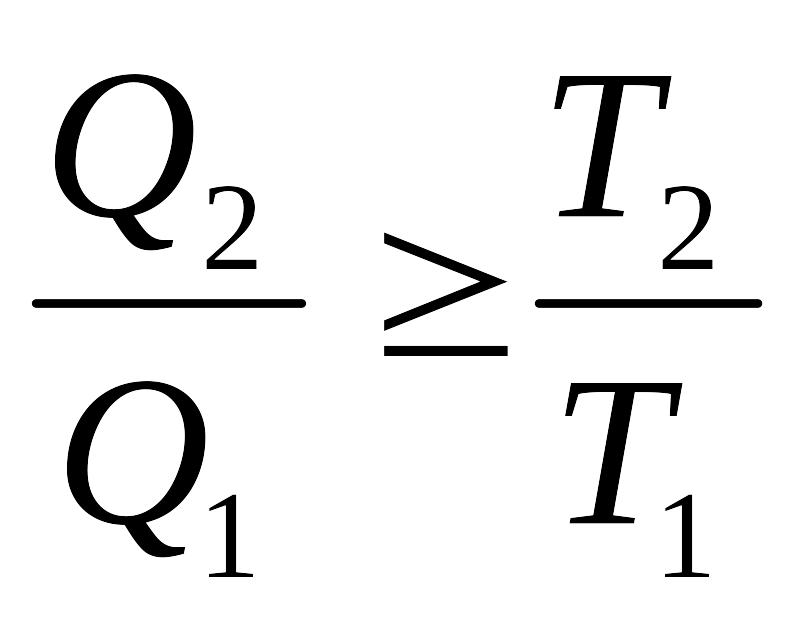 .
.
Теңсіздіктің
екі жағын
![]() бөлшегіне көбейтсек, келесі өрнектерді
аламыз
бөлшегіне көбейтсек, келесі өрнектерді
аламыз
![]() немесе
немесе
![]()
![]() немесе
немесе
![]()
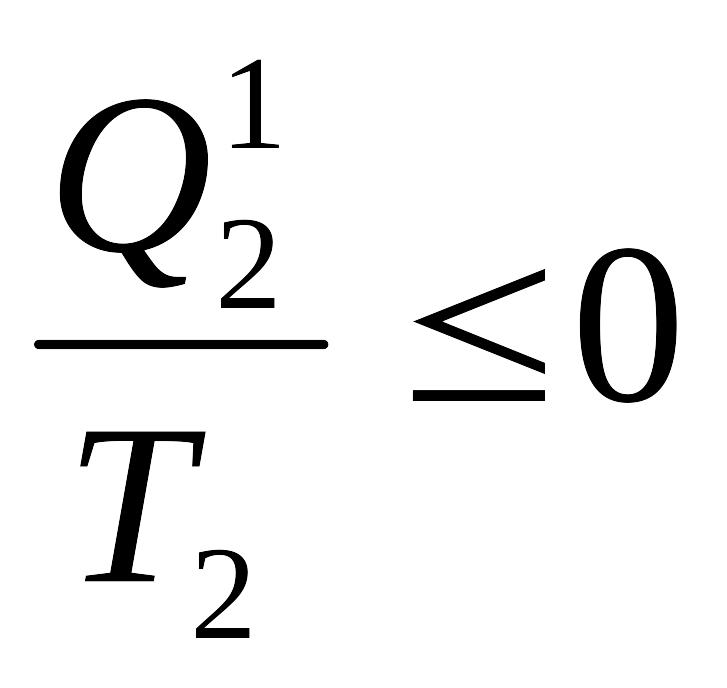 ,
,
Мұндағы
– суытқышқа берілген жылу мөлшері;
![]() – жұмыс денесінің суытқыштан қабылдаған.
Жүйенің қандай да бір денеден алған
жылу мөлшерінің сол дененің температурасына
қатынасын
– жұмыс денесінің суытқыштан қабылдаған.
Жүйенің қандай да бір денеден алған
жылу мөлшерінің сол дененің температурасына
қатынасын
![]() ,
Клаузиус, келірілген
жылу мөлшері
деп атады.
,
Клаузиус, келірілген
жылу мөлшері
деп атады.
Соңғы теңсіздік Клаузиус теңсіздігі деп аталады. Оның физикалық мағынасы: жүйенің циклде сырттан алған келтірілген жылуының элементар мөлшерлерінің қосындысы қайтымды циклдер үшін нөлге тең, ал қайтымсыз циклдер үшін нөлден кіші болады:
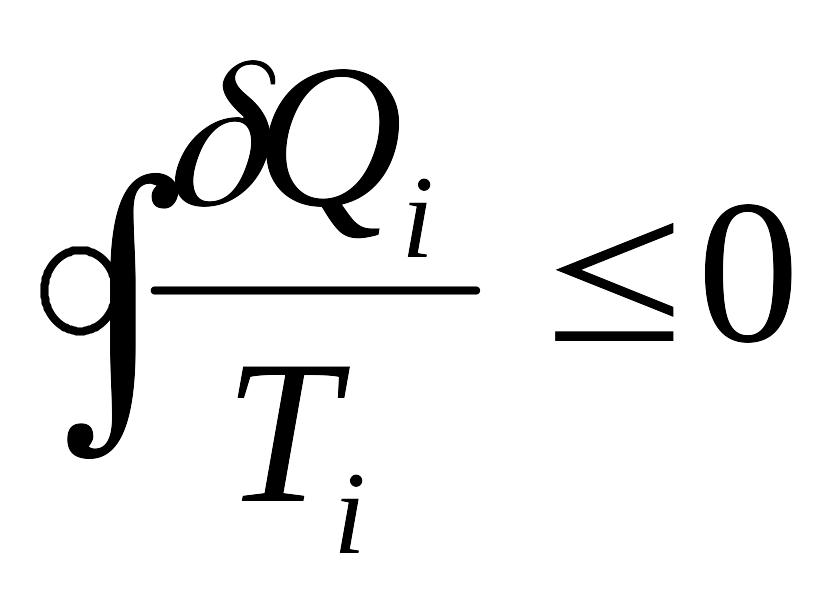 .
(9.6)
.
(9.6)
9.6 Энтропия
Жүйенің күйін аз шамаға өзгерту үшін оған қыздырғыштан берілетін элементар жылу мөлшері , ал қыздырғыштың температурасы Т болсын. Егер жүйедегі процесс қайтымды болу үшін, оның температурасы да Т болу керек. Қайтымды процесс кезіндегі келтірілген жылудың элементар мөлшерін dS арқылы белгілейік:
![]() ,
(9.7)
,
(9.7)
мұндағы S – энтропия. Жылу мөлшері Q процесс функциясы. Ал, энтропия S күй функциясы болады.
9.6.1 Энтропияның қасиеттері
1)
Энтропияның
өзгеру сипаты бойынша жылуалмасу
процесінің бағытын анықтауға болады.
(9.7) өрнектен
пен
таңбалары бірдей болатынын көреміз.
Олай болса, жүйеге жылу берілгенде (
)
оның энтропиясы өседі (![]() );
жүйеден жылу алынғанда (
)
оның энтропиясы кемиді (
);
жүйеден жылу алынғанда (
)
оның энтропиясы кемиді (![]() ).
).
2) Оқшауланған жүйенің энтропиясы қайтымсыз процестер кезінде тек қана өседі, қайтымды процестер кезінде тұрақты болып қалады. Олай болса, оқшауланған термодинамикалық жүйенің энтропиясы ешқашан кемімейді:
![]() .
(9.8)
.
(9.8)
3) Қайтымды адиабаталық процестер изоэнтропты (мұндай процестерде энтропия өзгермейді) болады.
Карно
циклі екі изотерма мен екі адиабатадан
(изоэнтроптан) тұрады. Бұл процестің
T-S
диаграммасы (9.5
– сурет)
қабырғалары координат өстеріне параллель
тік төртбұрыш болады.
![]() формуласы
бойынша,
қыздырғыштан
алынған
жылу
есебінен
өтетеін
1 – 2 изотермиялық
процесс
кезінде
жүйеге
берілетін
жылу
мөлшері
Q1
тең
болады:
формуласы
бойынша,
қыздырғыштан
алынған
жылу
есебінен
өтетеін
1 – 2 изотермиялық
процесс
кезінде
жүйеге
берілетін
жылу
мөлшері
Q1
тең
болады:
![]() ,
(9.9)
,
(9.9)
мұндағы S1 – жүйенің процесс басталар алдындағы энтропиясы, S2 – процесс соңындағы энтропия.
|
Изотермиялық 3 – 4 процесс кезінде суытқышқа берілетін Q2 жылу мөлшері тең болады:
Жүйенің бір циклде алатын жылу мөлшері
|
4) 9.1-кестеде идеал газдың әртүрлі процестерде 1 күйден 2 күйге өтулері үшін энтропияның өзгеру өрнектері келтірілген
9.1- кесте
Изохоралық ( |
Изобаралық ( ) |
Изотермиялық ( |
Адиабаталық ( |
|
|
|
|
Бұл өрнектер
 ,
(9.12)
,
(9.12)
формуладан шығады. Соңғы өрнек тепе-теңдікте процестердегі энтропия өзгерісін сипатайтын келесі формуладан алынған:
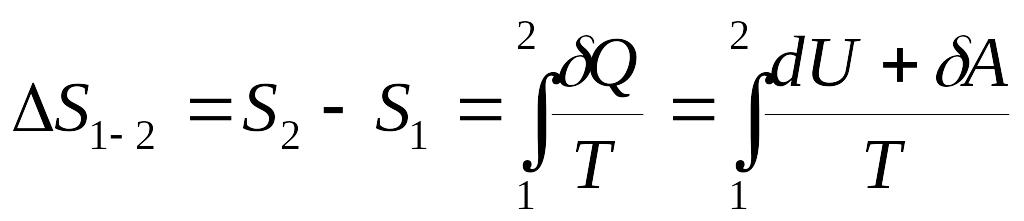 ,
,
мұндағы
![]() ,
,
![]() .
.
Өрнекті
алу үшін
![]() және
және
![]() қатынастары қоланылды.
қатынастары қоланылды.
5) Жүйенің байланысқан энергиясы.
Қайтымды
изотермиялық процесс кезінде жүйе
жұмысты
![]() еркін энергия есебінен атқарады:
еркін энергия есебінен атқарады:
![]()
немесе
![]() ,
(9.13)
,
(9.13)
мұндағы
![]() – жүйенің
еркін энергиясы
(Гельмгольц
энергиясы).
Мұндағы TS
ішкі энергияның қайтымды изотермиялық
процесс кезінде жұмысқа айнала алмайтын
бөлігі. Ішкі энергияның бұл бөлігін
байланысқан
энергия
деп атайды. Егер температура тұрақты
болса, онда жүйенің энтропиясы артқан
сайын оның байланысқан энергиясы да
арта береді.
– жүйенің
еркін энергиясы
(Гельмгольц
энергиясы).
Мұндағы TS
ішкі энергияның қайтымды изотермиялық
процесс кезінде жұмысқа айнала алмайтын
бөлігі. Ішкі энергияның бұл бөлігін
байланысқан
энергия
деп атайды. Егер температура тұрақты
болса, онда жүйенің энтропиясы артқан
сайын оның байланысқан энергиясы да
арта береді.
6) Энтропия – термодинамикалық жүйедегі күйлер ықтималдылығының өлшемі .
Жүйе
күйлерінің термодинамикалық ықтималдылығы
![]() осы күйдің жүзеге асырылу әдістерінің
санымен анықталады. Басқаша айтқанда,
белгілі макрокүй ықтималдылығы жүйенің
осы күйін тудыратын барлық мүмкін
микрокүйлер санына (микробөлшектердің
жылдамдықтар мен координаталар бойынша
жүйенің осы күйіне сәйкес келетін
таралуы) тең. Термодинамикалық
ықтималдылық W≥1,
сондықтан
ол бірден кіші болатын математикадағы
ықтималдылықтан өзгеше.
осы күйдің жүзеге асырылу әдістерінің
санымен анықталады. Басқаша айтқанда,
белгілі макрокүй ықтималдылығы жүйенің
осы күйін тудыратын барлық мүмкін
микрокүйлер санына (микробөлшектердің
жылдамдықтар мен координаталар бойынша
жүйенің осы күйіне сәйкес келетін
таралуы) тең. Термодинамикалық
ықтималдылық W≥1,
сондықтан
ол бірден кіші болатын математикадағы
ықтималдылықтан өзгеше.
Больцман
жүйенің термодинамикалық
ықтималдылығы
мен
энтропиясы
![]() арасында келесі тәуелділік бар екенін
дәлелдеді:
арасында келесі тәуелділік бар екенін
дәлелдеді:
![]() .
(9.14)
.
(9.14)
Бұл Больцман формуласы. Жүйенің қандай-да бір күйініің энтропиясы осы күйді тудыратын микрокүйлер санының логарифмімен анықталады.

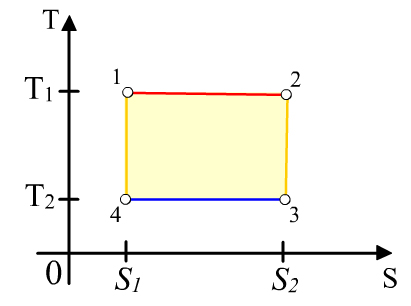 9.5
– сурет. Карно цикліндегі жұмыс
9.5
– сурет. Карно цикліндегі жұмыс