4.3 Импульс моментінің сақталу заңын дәлелдеу

Өз осі бойынша шеңбердің қозғалысын қарастырайық. Кір көтерген адам қолын екі жаққа керіп жылдамдықпен айналдырып отыр. Адамның инерция моменті тең. Адам жүкті айналу осьіне жақындатқанда инерция моменті азаяды. Бұл бұрыштық жылдамдықтың артуына әкеліп соғады, яғни (4.13) теңдігі бойынша , және .

4.1-кестеде дененің ілгерілемелі және айналмалы қозғалысының негізгі теңдеулері келтірілген.

4.1-кесте

Ілгерілемелі қозғалыс		Айналмалы қозғалыс
Масса		Инерция моменті
Күш		Күш моменті	; ;
Импульс		Импульс моменті	;
Динамиканың негізгі теңдігі		Динамиканың негізгі теңдіктері
Жұмыс		Жұмыс
Кинетикалық энергия		Кинетикалық энергия

Арнайы салыстырмалы теорияның элементтері

Классикалық механика заңдарын жарық жылдамдығына жақын жылдамдықпен қозғалатын денелер үшін қолдануға болмайды. Жылдамдығы жоғары денелердің қозғалысы арнайы салыстырмалылықтың теория механикасымен сипатталады. Арнайы салыстырмалылықтың теорияның негізін Эйнштейн тұжырымдаған екі постулат құрайды.

1. Табиғаттың барлық заңдары бір инерциалды санақ жүйесінен екінші инерциалды санақ жүйесіне өтуіне қатысты өзгермейді (инвариант болады).

2. Жарықтың вакуумдағы жылдамдығы барлық инерциалды санақ жүйелерінде бірдей және жарық көзі мен қабылдағыштың қозғалу жылдамдығына тәуелсіз.

Бұл постулаттардан төмендегі өте маңызды салдарлар келіп шығады:

1. Ұзындықтың қысқаруы

,

2. Массаның артуы

,

3. Уақыттың баяулауы

,

4. Жылдамдықтарды қосу ережесі

,

5) Дененің толық энергиясы

,

мұндағы индексінде «0» бар физикалық шамалардың мәндері тыныштық күйдегі санақ жүйесіне сәйкес келеді. Бұл постулаттар мен одан шыққан салдарлардың тәжірибеде дәлелдеу салыстырмалылық теориясына негізделген.

Эйнштейн постулаттарынан уақыт мерзімінің салыстырмалы қасиетке ие екендігі көрінеді, яғни әр түрлі инерциал санақ жүйелерінде уақыттың өтуі әр түрлі болады (жылдам немесе баяу). Эйнштейн бір санақ жүйесінен екінші санақ жүйесіне өтудегі түрлендіруді зерттей отырып, оның постулаттарының Лоренц түрлендірулеріне толық сәйкес екендігін дәлелдеді. Лоренц түрлендірулері мына түрде анықталған:

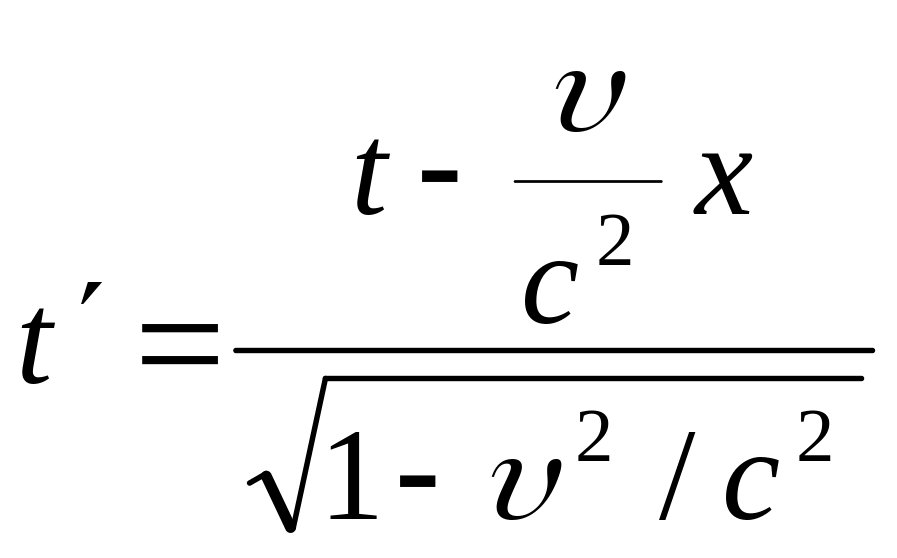, , , . (4.14)

Лоренц түрлендірулері аз жылдамдықтар кезінде Галилей түрлендірулеріне өтеді. Шындығында да егер болса (4.14) мына өрнекке айналады.

, , , . (4.15)

Сондықтан кезіндегі Галилей түрлендірулері Лоренц түрлендірулерінің шекті жағдайы болып табылады. Лоренц түрлендірулері К және К жүйелеріндегі координаттар мен уақыттың тәуелділігін өрнектейді. Бұл түрлендірулерді К жүйесіндегі координаттар мен уақытты штрихталған санақ жүйесіндегі координат мен уақыт арқылы жазуға болады.

, , , . (4.16)