Определение средней величины и квадратических отклонений
Средние величины (Х) находят по формуле:
,
где ∑ - символ суммы; х1, х2…- значение отдельных измерений; п - общее число случаев.
Получение средней величины рассмотрим на примере: У девушек (10 человек) и юношей (10 человек) определяли массу тела (табл.1).
Таблица 1
Масса тела (в кг) у девушек (а) и юношей (б)
№ п/п |
А |
Б |
№ п/п |
А |
Б |
1 2 3 4 5 |
58 53 56 55 57 |
65 68 60 64 71 |
6 7 8 9 10 |
52 49 54 56 50 |
67 66 72 74 63 |
Подставляем в формулу отдельные значения и получаем средние величины ХА и ХБ :
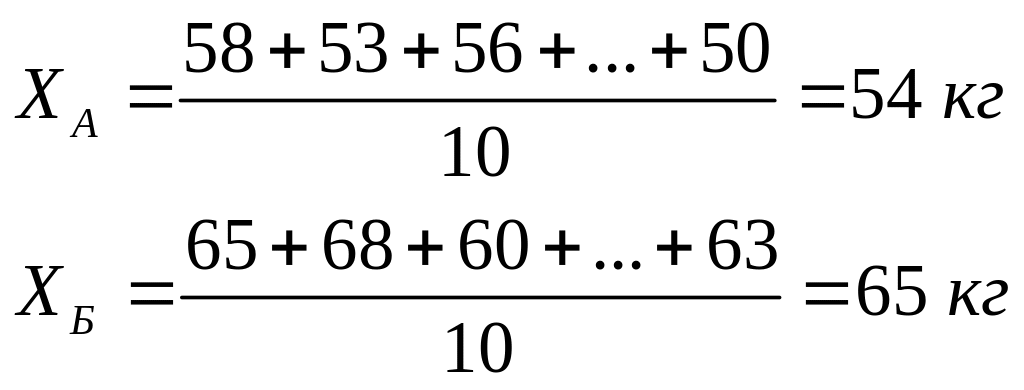
Средняя арифметическая величина является важной характеристикой признака. Однако при одной и той же средней величине наблюдаемые от нее отклонения могут варьировать в разной степени. Поэтому необходимо ввести показатель вариабельности признака. Таким показателем является среднее квадратическое отклонение (σ), которое находят по формуле
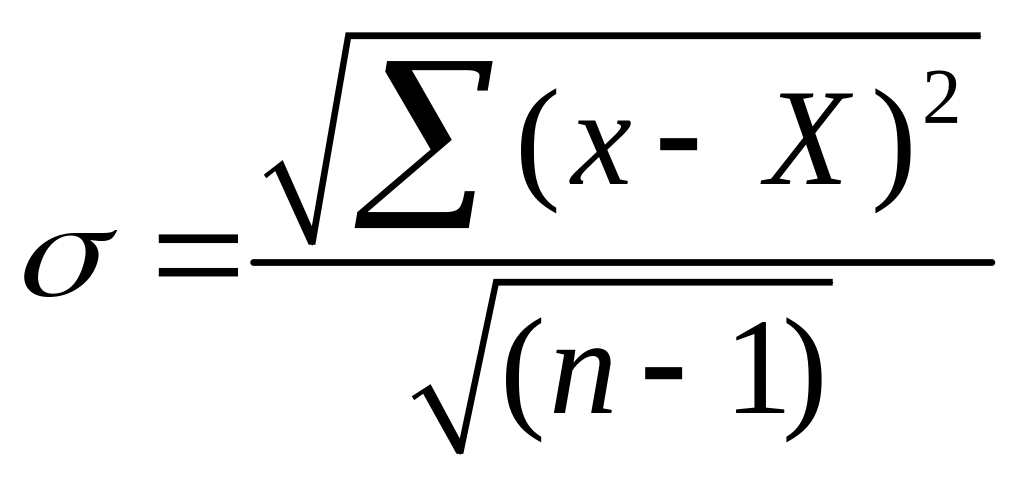
В числителе извлекается квадратный корень из суммы квадратов отклонений значений от средней арифметической; в знаменателе извлекается квадратный корень из разности (п-1), где (п-1) – число степеней свободы, равное числу наблюдений без одного.
Произведем соответствующие расчеты (таблице 2).
Таблица 2
Расчеты средних квадратических отклонений для групп
девушек (А) и юношей (Б)
Группа А |
Группа Б |
||
х-ХА |
(х-ХА)2 |
х-ХБ |
(х-ХБ)2 |
58-54=+4 53-54=-1 56-54=+2 55-54=+1 57-54-+3 52-54=-2 49-54=-5 54-54=0 56-54=+2 50-54=-4 |
16 1 4 1 9 4 25 0 4 16 |
65-67=-2 68-67=+1 60-67=-7 64-67=-3 71-67=+4 67-67=0 66-67=-1 72-67=+5 63-67=-4 74-67=+7 |
4 1 49 9 16 0 1 25 49 16 |
Итого: |
80 |
Итого: |
170 |
Из наших расчетов мы получили:
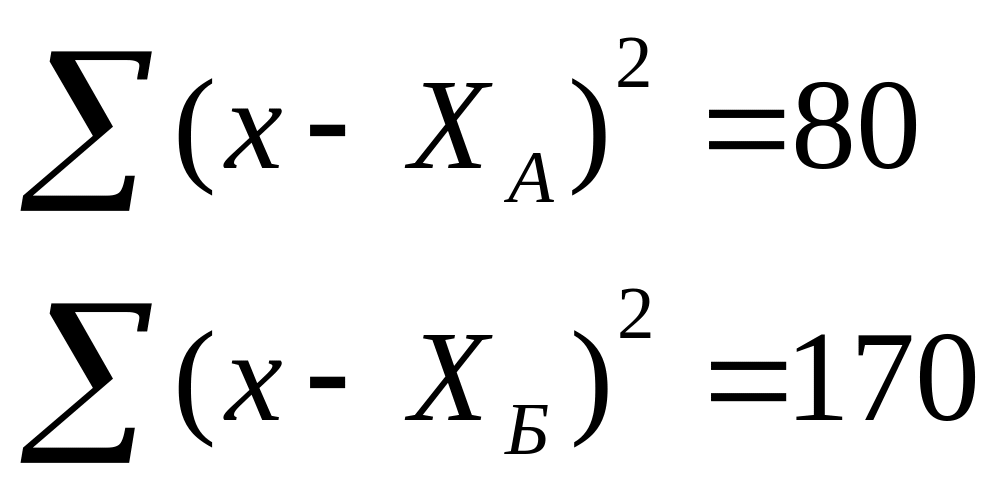
Следовательно,
Таким образом, мы получили данные о том, что масса тела у девушек в среднем равна 54+2,98 кг, а у юношей – 67+4,3кг.
Определение достоверности различий по критерию t-Стьюдента
Получив средние величины и квадратические отклонения, можно определить достоверность различий между двумя обследованными группами по критерию t-Стьюдента.
С этой целью можно применить формулу
,
где: Х-средняя величина;
m – ошибка средней, которую рассчитывают по формуле:
Если в нашем случае мы разделим σА (полученную для группы А) на квадратный корень из 10 (количество обследованных), то получим ошибку средней для группы А:
Ошибка средней для группы Б:
Получив значения ошибки средней для двух групп, подставляем их в формулу критерия t-Стьюдента:
В большинстве биологических исследований достоверность считается доказанной при 95%-ном уровне значимости. Это свидетельствует о том, что различия средних величин (в нашем случае – массы тела) возникли в результате недостатка числа наблюдений, составляющих меньше 5%. В таких случаях говорят, что вероятность ошибки p меньше 5%, т. е. p < 0,05.
Для того чтобы определить достоверность различий, необходимо обратиться к специальной таблице, в которой представлены граничные значения критерия t-Стьюдента для 5%-ного уровня значимости в зависимости от числа степеней свободы (табл. 3).
В нашем примере критерий t-Стьюдента равен 7,97, а число степеней свободы n=(nА+nБ)–2, т. е. (10+10) –2=18.
Из таблицы 3 видно, что граничным значением для 18 является 2,1. Наша цифра значительно превосходит эту величину, следовательно, обнаруженные нами различия в массе тела девушек и юношей достоверны.
Таблица 3
Граничные значения критерия Стьюдента для 5%-ного уровня значимости
n |
0,05 |
n |
0,05 |
n |
0,05 |
2 |
4,30 |
18 |
2,10 |
50 |
2,01 |
4 |
2,78 |
20 |
2,09 |
60 |
2,00 |
6 |
2,45 |
22 |
2,07 |
70 |
2,00 |
8 |
2,31 |
24 |
2,06 |
80 |
1,99 |
10 |
2,23 |
26 |
2,06 |
90 |
1,99 |
12 |
2,18 |
28 |
2,05 |
100 |
1,98 |
14 |
2,15 |
30 |
2,04 |
120 |
1,98 |
16 |
2,12 |
40 |
2,02 |
200 |
1,97 |