§4. Үздіксіз бөлшектер арқылы айқындалған теңдеудің

бір пар түбірлерін шығару

Үздіксіз бөлшектер ережесі арқылы біз

(4.1)

түрдегі көмескі теңдеудің бір пар түбірін шығаруға еріктеміз. Мысалы, бізде

(4.2)

теңдеуі бар екен. Оны шешпестен бұрын біз бөлшегін үздіксіз түрге мінгізелік. Ал

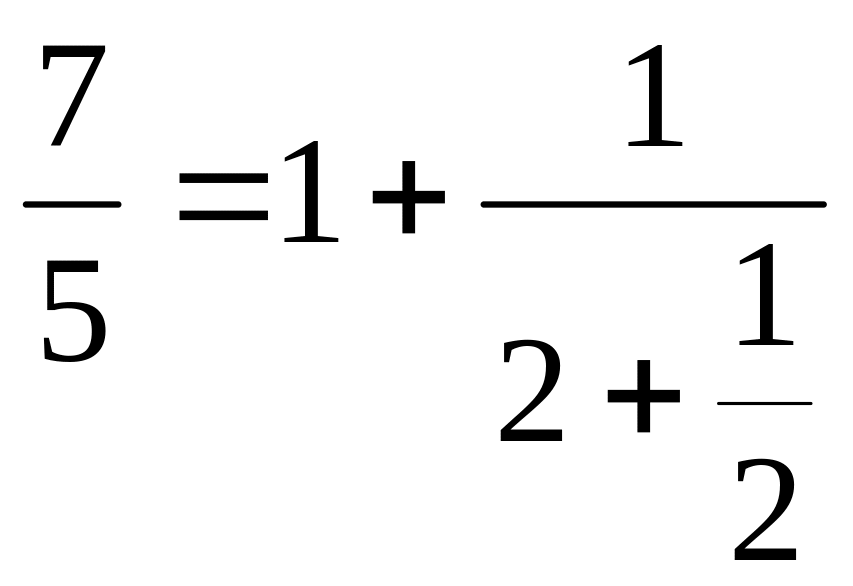_(4.3)

түрінде болатындығы мәлім нәрсе. Енді соңғы үздіксіз бөлшектің аяғынан екінші жуықтас бөлшегін табалық (аяғынан бірінші жуықтас бөлшек берілген -нің өзі болатындығы белгілі). Ол шамасында болатындығы айқын. Табылған жуықтас бөлшегі жұп орында тұрғандағы үшін оның шамасы берілген ден артығырақ болып, арасындағы айырма шамасында болатын еді. Сондықтан

_(4.4)

өрнегі жасалады. (4.4)- ші теңдікті берілген көмескі теңдеуге ұқсас қылу үшін соңғы теңдіктің бар мүшелерін 13-ке өсіріп, мына түрде жазалық , яки

(4.5)

Енді (4.5)-ші теңдік пен берілген теңдеуді салыстырсақ, тің орнына , тің орнына 39 алсақ, олар өзара дәл шығып отыр. Олай болса, теңдеуінің бір пар түбірі табылды, ол: . Сондықтан енді теңдеуінің бар түбірлерін табуға мүмкін.

Олар

тізімдері арқылы табылмақшы. санында шарт мәні болмайтындығы үшін, жоғарғы тізімде теңдеуін шарт қылсақ, түбір тізімдері мына сияқты қолайлы түрге мінбекші:

2-мысал: Бізде теңдеуі бар екен. ні үздіксіз бөлшекке аударалық. Онда

болмақ. Аяқтан екінші жуықтас бөлшекті табалық, ол екен. Алған жуықтасымыз тақ орында тұрғандығы үшін оның маңызы ден кем болмақ. Сондықтан

Бұдан дәлдігі жасалады. Соңғы дәлдіктің мүшелерін 5-ке өсірсек өрнегі арқылы берілген теңдеудің бір пар түбірі табылады. Олар

Сондықтан берілген теңдеудің бар түбірлерінің мәні

тізімдерінен табылмақ.

саны шартты мәнге ие болатындығы үшін ні мен ауыстырсақ, алдыңғы тізімдер

түрлеріне мінеді.

ІІ бөлім

§1. Үздіксіз бөлшек және күнтізбе

Барлығымыз білетіндей 1жыл=365 күн 5 сағат 48 минут 46сеунд=365,242199...күн. Күн тәулігімен өлшенген, күн жылының бөлшектері оның ұзындығына сәйкес келеді. 365, 242199…=365;4,7,1,3,5,…- күндік күнтізбе жасауға мүмкіндік береді.

Б ірінші жуықтас бөлшек 36514 юлиандық күнтізбеге сәйкес келеді, әр төрт жыл сайын кібісе(високосный) жыл болады. Төмендегілердің арасындағы айырмашылықтарын анықталық,

365,25-365,242199=0,007801тәулік=0,187224сағат=11,23344минут=11минут 14секунд, яғни жылдың орташа ұзындығы қазіргіден 11 минут 14 секндқа артық. Үшінші жуықтас бөлшек 365;4,7,1=365833 парсы күнтізбенің негізі болды. Бұны 1079 жылы математик, астроном және ақын Омар Хайям ұсынды. Бұл жердегі 365833-365,242199=0,000225242тәулік=0,005406сағат=0,324348минут=19,5секунд арасындағы айырмашылығын тапсақ, яғни бір жылда 19секундқа қателесеміз, бірақ жылдарды 33-жылдық циклге шақсақ, әрбір төрт жылдан кейінгі кібісе(високосный) жылдың ішіндегі цикл жеті рет саналады, ал сегізінші, бесіншіде ыңғайлы емес. Яғни ІІІ-ІІІ-ІІІ-ІІІ-ІІІ-ІІІ-ІІІ-ІІІ-ІІІ-ІІІ-ІІІ(Бұл жердегі таяқшаларжылдарды білдіреді, ал сызылғандары кібісе жылдарды білдіреді).

1864 жылы орыс астрономы Иоганн Генрих Медлердің айтуынша төртінші жуықтас бөлшек 365, 24199…=36531128 тағы да бір күнтізбені береді. Медлер осыны ХХ ғасырда Россияда ұсынды. Бұл үшін әрбір 128 жыл сайын 1 кібісе жылды өткізу керек болды, себебі юлиандық күнтізбе бойынша әрбір 128 жылға 32 кібісе жыл келді. Бұл күнтізбе қабылданбады, өйткені 128 саны дөңгелек емес (не круглое) Бұл жердегі қателігіміз неде?

36531128-365,242199=-0,0000115 тәулік = -0,000276 сағат = -0,01656 минут = -0,99 секунд = -1секунд!

Яғни бұл күнтізбе жылдық қате 1 секундты құрайды.

1582 жылы ХІІІ папа Григорий юлиан күнтізбесінің дәлсіздігін түзетіп реформа енгізді. Сонымен қоса жай және кібісе(високосный) жылдардың кезектесуі өзгермеді, егер де нөмір екі нөлмен аяқталса, ал сан төртке бөлінсе, бұл жай жыл. Мысалы, 1500 жай жыл, ал 1600 кібісе жыл.

Христов жаңа жылынан бастап қате 10 күн жиналды(1700, 1800, 1900жылдар). Юлиан күнтізбесімен 13 күн сәйкес келмейді. Енді григориан жылының ұзақтығын есептейміз. Юлиан күнтізбесі бойынша 400 жылдың 100 жылы кібісе, ал григориан бойынша 97, сондықтан григориан жылының орташа ұзақтығы 36597400 тәулік = 365,2425 тәулік = 365 тәулік 5сағат 49минут 12секунд, ол қазіргіден 26секундқа артық. Оңтүстік – Шығыс Азия, Иран, Израиль елдерінде ай – күнтізбесінің бірнеше түрі бар.