§3. Үздіксіз бөлшектердің кейбір қолданулары

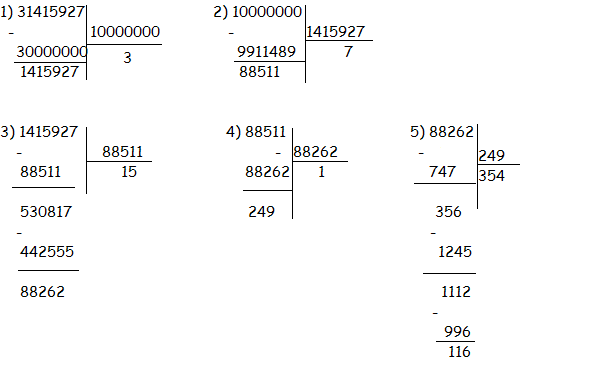
Егер берілген бөлшектің бөлгіші мен жарнағы аса үлкен сандар болса, кей мезгілде оның шын маңызына жуықтас болған жеңіл санды бөлшектерді алу қолайлырақ болады. Бұл үшін берілген бөлшекті үздіксіз бөлшекпен ауыстырып, оның орнына ішіндегі қалаған жуықтас бөлшектің бірінің шамасын қолдануға керек. Мысалы, бізге шеңбер мен оның диаметрінің арасындағы шын шамасы 3,1415926 мен мен 3,1415927 бөлшектерінің аралығында болса және ізделген еселікті π (яки басқаша пи) –мен белгілесек жазуға жеңіл және шын шамасына жуықтас болған π—дің мәндерін табу үшін біз әуелі алдыңғы бөлшектерді үздіксіз бөлшек түріне аударалық

Олай болса, берілген бөлшектер

түріне ауады. Соңғы табылған екі үздіксіз бөлшектердің өзара ортақ еселіктерін ғана алсақ, π—дің

бөлшегімен тең екендігін табамыз. Онда π—дің ең алғаш жуықтас бөлшектері мынау болар еді.

		15	1
3	22	333	355
1	7	106	113

бөлшектері екен.

π—дің мәнді жуықтас шамасын тапқан Архимед деген ғалым, π—дің орнына оны алғандағы істейтін қатеміз ден кемірек болмақ. π—дің орнына алғандағы істейтін қатеміз:

бөлшегінен гөрі кем болмақшы.

Архимед пен Мешийдің алған жуықтак бөлшектері жұп, орындарда тұрғандығы үшін екеуінің шамасы шынында . π—ден артығырақ.

Квадрат түбір шығару

Бізге 13-тен шаршы түбір шығару мәселесі берілсін. Бұл үшін біз төмендегі жобаны қолданалық: 1) 13-тің ішіне кіретін ең үлкен шаршылық түбір 3 болмақ, өйткені 4-ті алсақ, болып, оның шаршылық дәрежесі берілген саннан артып кетер еді.

1. Енді біз

(3.1)

теңдігі орынды болсын делік. Олай болса,

_(3.2)

өрнегі арқылы

_(3.3)

теңдігі орынды болады екен.

_{(3.3)-ші теңдіктің шамасы бір бөлшекті қосумен тең болатындығы үшін}

_(3.4)

_{теңдігін жасауға еріктіміз, онда}

_{өрнегі арқылы}

_(3.5)

теңдігі жасалмақ. Енді (5)-ші теңдіктің маңызын 1-ге бір бөлшек қосқанда тең болатындығып абайлап:

_(3.6)

өрнегін жасалық. Онда

_(3.7)

өрнегі арқылы

_(3.8)

теңдігі шықпақ. (3.8)-ші теңдікті жоғарғы жобамен

_(3.9)

түріне аударсақ, онда

болып

өрнегі табылады. Соңғы теңдікті

түріне аударып, онан

_(3.10)

теңдігін табамыз. Соңғы теңдікте

_(3.11)

өрнегі орындалмақ. (3.11)-ші өрнекті тағы да

_(3.12)

түріне мінгізсек, одан

_(3.13)

теңдігі табылмақшы. (3.13)-ші теңдік пен (3.2)-ші теңдікті салыстырсақ яки екендігін білеміз. Олай болса, (3.1), (3.4), (3.6), (3.8), (3.9), (3.12) теңдіктері арқылы біз

_(3.14)

бөлшегін жазуға еріктіміз. Мұнан енді - тің шаршы түбірі қиырсыз және қайталама үздіксіз бөлшектің түріне мініп отыр. Мұнда(1,1,1,1,6) еселігі қиырсыз қайталанып отырады екен. (3.14)-ші үздіксіз бөлшектің әрбәр жуықтас бөлшектері әрине - тің де жуықтас түбірлері болып отырмақшы. Олар:

			1	1	1	1	6	1
	3	4	7	11	18	24	192	221
	1	1	2	3	5	8	53	61

түрінде болмақ.