3 Классификация

Классификацияның теориялық негіздері

Классификация дәндердің еркін немесе қысымды құлауы кезінде жүзеге асады. Еркін құлау ортадағы дәндердің бір – бірінен өзара әсерлесуін болдырмайтын бірлік дәндерінің қозғалысынан тұрады. Қысымды құлау нәтижесінде дәндер қозғалысына айналасындағы дәндердің динамикалық әсері болатын гравитационды күш пен ортаның кедергі күші әсерінен көптеген дәндердің массаларымен түсіндіріледі.

Дәндердің еркін құлауының жылдамдығы ауырлық күштері, көтеру (Архимедті) күштері мен дәндер қозғалысының режиміне қатысты ортаның кедергі күштері қатынасымен анықталады.

Ламинарлы режим кезінде дене аз жылдамдықпен қозғалады, ортаның ағыны оны жуып тазалайды. Кедергі Р_в ортаның жабысқыштығымен μ анықталады және сандық түрде Стокс заңымен сипатталады.:

Рв = 3 πμνd (1)

мұндағы ν – дәндердің қозғалыс жылдамдығы; d – дәндер диаметрі.

Турбулентті режим қозғалыстың жоғарғы жылдамдығымен сипатталады және дене бетіндегі және оның соңдарында вихрладың пайда болуымен шығарылады. Денелердің орын ауыстыруымен болатын ортаның динамикалық және инерционды кедергі бұл жағдайда Ньютон – Риттингердің заңымен өзгереді:

мұндағы k – коэффициент (1/2 – ге тең, Риттингер бойынша); F – денелер проекциясының ауданы (шар үшін πd² – қа тең); Δ – ортаның тығыздығы.

Шынайы жағдайда қозғалмалы дәндер бір уақытта жабысқақтықтан кедергіні Р_в және динамикалық кедергіні Р_д сезеді. Р_в, Р_д кедергілерінің күштерінің қатынастарының сипатына, кезекті түрде ортадағы минералды дәндердің режиміне Рейнольдстың өлшемсіз параметрлері (Re) жатады:

бұдан жалпы түрде:

Re < 1 болған кезде, өлшемдері 0,1 мм – ден аспайтын бөлшек қозғалыстарының ламинарлы режимі байқалады. Re > 1 және бөлшектер өлшемдері 2 мм - ден көп болған кезде, қозғалыстың турбулентті режимі байқалады. Қозғалыстың ламинардан турбулентті режиміне өту ауданына Re шамасы 1 – ден 1000 – ға дейін, ал бөлшектер ірілігі 0,1 – ден 2 мм – ге дейін жатады. Бұл облыс үшін ортаның кедергісін Аллен формуласымен есептеуге болады:

Егер μ шамасын (3) формуладан (1) теңдеуге қоятын болсақ,

және Р_д теңдеуі үшін [(2) формуласы], Р_а үшін [(4) формуласы], Р_в үшін [(5) формуласы] салыстыратын болсақ, онда дәндердің қозғалысына ортаның кедергісінің заңы былайша жазылады:

мұндағы φ=f(Re) – кедергі коэффициенті. Логарифмдік координаттарда φ=f(Re) – ның графикалық бейнеленуі Рейлей диаграммасы деп аталады (5 – сурет, φ қисығы), қозғалыстың ламинарлыдан турбулентті режимге өтуінің тұрақтылығын көрсетеді. Дәндердің құлауын туғызатын гравитационды күш G ортадағы дененіңсалмағымен анықталады. Архимед заңына қатысты көлемі болатын шар тәрізді денелерде:

мұндағы δ – дәннің тығыздығы; g – ауырлық күшінің жылдамдауы.

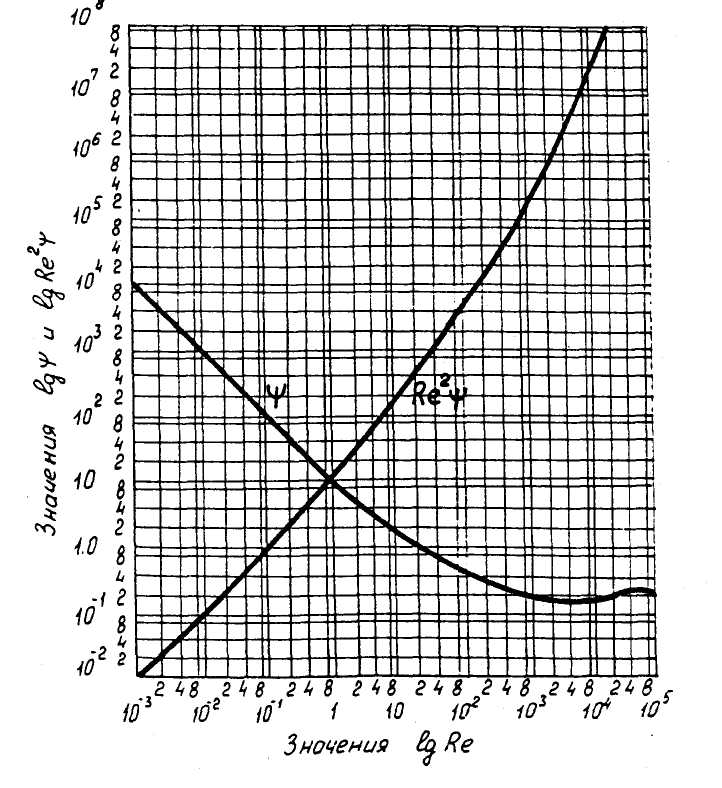
2.5 – сурет – Кедергі коэффициентінің Ψ және параметрінің Re ² Ψ Рейнольдс санынан Re тәуелділігі

Ортада дәндердің жылдамдығын арттыратын қорытынды күш Р₁ гравитационды күшпен G және кедергі күшінің Р арсындағы айырмашылықпен анықталады [(7) формуласы]:

Бастапқы кездегі гравитационды күш әсерінен бөлшектердің қозғалысының жылдамдығының артуы ортаның кедергісінің жоғарлауын тудырады және доли секунд арасында бөлшектер тұрақты жылдамдықпен ν₀ құлай бастайды.Бұл жағдайда

бұдан (жалпы жағдай үшін):

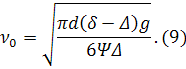
Ламинарлы режимде, (1) және (8) теңдеулердің негізінде:

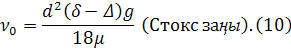
Ауыспалы режим кезінде, (4) және (8) теңдеулер негізінде:

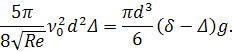
Re үшінгі теңдеуді есептегенде:

Турбулентті режимде, формулалардың негізінде:

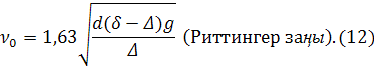
Кез келген ірілікті, тығыздықты, формалы дәндердің қозғалысының жылдамдығының соңғысын анықтауға арналған универсалды әдісті П. В. Лященко ұсынды. Ол (3) және (6) формулаларын ескере отырып, теңдеулер жүйесін құрды:

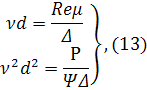
ортақ есептеу нәтижесінде Re²Ψ параметрі үшін теңдеу аламыз:

Р = G орнатылған қозғалысы болған кезде, (3.18) формуласындағы Р орнына (3.11) формуласынан G арналған теңдеуді табамыз:

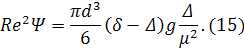
Дәндер мен ортаның белгілі параметрлері негізінде (15) теңдеу көмегімен Re²Ψ параметрінің шамасын анықтауға болады және оны 1 – суретте көрсетілген Рейлей диаграммасының Ψ=f(Re) негізінде құрылған Re²Ψ=f(Re) диаграммасы бойынша Рейнольдстің параметрлерін анықтау үшін қолданады. Бұдан соң бөлшектердің құлауының соңғы жылдамдығын анықтауға болады немесе Re – алынған шамасын 3 формулаға қою арқылы немесе Рейлей диаграммасындағы Re шамасымен табылған Ψ шамасын (9) формулаға қою арқылы анықтауға болады (1 – суретті қара, Ψ қисығы).

Ұсынылған әдебиеттер:

1. Кендерді байытуға арналған справочник; М., Недра, 1983.

2. А. А. Абрамов, С. Б. Леонов. «Түсті метал кендерін байыту», М., Недра, 1991.

3. А. А. Абрамов. Қатты пайдалы қазбаларды жинақты қолдану және байыту, қайта өңдеу. М. МГТУ, 2004, 509 бет.

4. Кендерді байытуға арналған справочник. Негізгі процестер. М., Недра, 1983.

СӨЖ арналған бақылау сұрақтары (2 тақырып)

1. Тәжірибеде елеуіштерді таңдау қандай негізде жүргізіледі?

2. Елеу процестерінде електерді таңдау қандай негізде жүргізіледі?

3. Қандай өнім тор асытылық, қайсысы решетка үстілік деп аталады?

4. Елеу шкаласы деп нені айтады?

5. Қандай жағдайда елеу шкаласын қөмекші деп атайды?