1.2. Основные свойства неопределенного интеграла

Рассмотрим основные свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции, т. е.:

Доказательство. Так как где 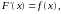то дифференцируя левую и правые части этого равенства, получаем:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т. е.:

Доказательство. По определению дифференциала и свойству 1 имеем:

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т. е.:

где с – произвольное число.

Доказательство. Рассматривая функцию как первообразную для некоторой функции , можно записать

и на основании свойства 2 дифференциал неопределенного интеграла поэтому имеем

4. Постоянный множитель можно выносить за знак интеграла, т. е.

где  – некоторое число.

Доказательство. Пусть F(х) – первообразная для функции f (х), т. е.

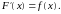
Тогда F(х) – первообразная для функции f (х):

Из определения следует, что

где с₁ = с.

5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций, т. е.:

Доказательство. Пусть и – первообразные для функций и , т. е. Тогда функции являются первообразными для функций 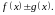Следовательно,

6. Неопределенный интеграл не зависит от переменной интегрирования, т. е., если выполняется:

то будет справедливо

1.3. Таблица основных интегралов

_{Запишем таблицу основных интегралов.} Так как действия дифференцирования и интегрирования являются взаимно обратными, то простейшую таблицу интегралов можно получить обращением таблицы производных. Дополним эту таблицу интегралами, наиболее часто встречающимися на практике. Заметим, результат интегрирования всегда можно проверить дифференцированием: если то

№ п/п	Интеграл	№ п/п	Интеграл
1		10
2	при	11
3		12
4		13
5		14
6		15
7		16
8		17
9		18
19		22
20		23
21

Приведенные в таблице интегралы назовем табличными, их необходимо знать наизусть.

В интегральном исчислении нет общего приема нахождения неопределенного интеграла. При интегрировании функций разными методами в конечном итоге интегралы всегда будут приводиться к одному или нескольким табличным. Рассмотрим методы интегрирования функций.