2.4.2. Эквивалентность ставок различных видов

При проведении финансово-экономических расчетов часто пользуются эквивалентными ставками, когда по заданному значению ставки одного вида находят эквивалентное значение ставки другого вида.

Эквивалентными считаются процентные ставки различного вида, применение которых в однотипных по значению операциях дает одинаковые финансовые результаты. Например, сравнение дохода, полученного от вклада с начислением процентов по простой ставке, с доходом, который мог бы быть получен при начислении процентов по номинальной ставке; сравнение дохода, получаемого от учета векселей, с доходом от депозитных операций и т.д.

Основой для определения значений эквивалентных процентных ставок является уравнение эквивалентности для соответствующих финансовых операций. Методика составления уравнений эквивалентности заключается в следующем. Сначала выбирается величина, выражение для которой в данной финансовой операции можно получить с помощью ставок различного вида. Затем на основе равенства выражений для выбранной величины составляется уравнение эквивалентности. Из этого уравнения с помощью математических преобразований можно получить зависимости между ставками различного вида, обеспечивающими эквивалентность данной финансовой операции.

Эквивалентность простых процентных и простых учетных ставок. Для определения простой ставки процентов и учетной ставки в качестве сравниваемой величины можно взять сумму процентных денег при выдаче ссуды. Сумма процентных денег при выдаче ссуды на п лет при использовании простой ставки процентов определяется выражением I = Р ∙ I ∙ п, а при использовании простой учетной ставки — выражением D = S ∙ d ∙ n.

Приравнивая эти выражения, получаем уравнение эквивалентности:

Заменим значение S выражением (2.54).

Случай 1. Если срок ссуды измеряется годами, то

Отсюда

Выражения (2.72) и (2.73) представляют собой зависимости между эквивалентными простыми ставкой процентов и учетной ставкой, обеспечивающими одинаковую эквивалентность ссудной операции (одинаковую сумму процентных денег).

Случай 2. Если срок ссуды измеряется в днях, то

где K_t и K_d — значения временной базы при использовании ставки процентов и учетной ставки (эти значения могут быть различными).

Отсюда

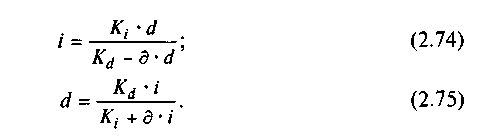
Полученные эквивалентные ставки i и d могут быть использованы при сравнении доходности сделок, в которых применяются различные виды ставок. Из приведенных формул легко заметить, что с уменьшением п (д/К) различие между эквивалентными ставками i и d становится менее заметным. Например, для d = 10% эквивалентные значения i равны:

Эквивалентность простых и сложных процентных ставок. Для определения эквивалентных значений простых и сложных процентных ставок составим уравнение эквивалентности:

где i_пр — ставка простых процентов; i_сл — ставка сложных процентов.

Отсюда найдем ставку простых процентов, эквивалентную ставке сложных процентов:

Ставка сложных процентов, эквивалентная простым, находится по формуле

Из выражений (2.77) и (2.78) следует, что эквивалентные ставки существенно зависят от срока начисления процента (n).

ПРИМЕР 11. Допустим, кредит предоставляется из расчета 60% сложных годовых.

Какова должна быть эквивалентная ставка простых процентов при сроке кредита: а) n = 3 года; б) п = 6 месяцев?

Решение. По формуле (2.77) находим:

Вывод. Чем больше срок начисления сложных процентов, тем выше эквивалентная ставка простых процентов.

ПРИМЕР 12. Допустим, кредит предоставляется из расчета 60% простых годовых. Какова должна быть эквивалентная ставка сложных процентов при сроке кредита: а) п = 4 года; б) п — 6 месяцев?

Решение. По формуле (2.78) находим:

Вывод. Чем больше срок начисления простых процентов, тем ниже эквивалентная ставка сложных процентов.

Эквивалентность простой и сложной номинальной ставок. При определении эквивалентных значений простой и номинальной ставок процентов используют следующее уравнение эквивалентности:

Отсюда получим:

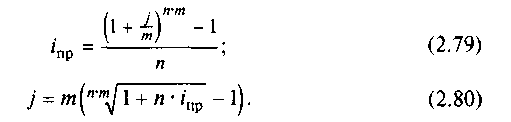
Эквивалентность простой учетной ставки и сложной ставки годовых процентов. При определении эквивалентных значений простой учетной и сложной ставок начисления годовых процентов уравнение эквивалентности в соответствии с формулами (2.22) и (2.54) будет иметь вид

где n_d = д/K_d — период начисления учетной ставки; n_i = д/K_i — период начисления процентной ставки; K_d; K_i — временные базы для начисления процентов по учетной и процентной ставкам, которые могут быть различными.

Отсюда

или

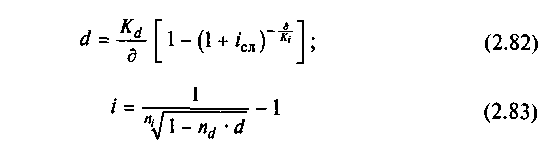
или

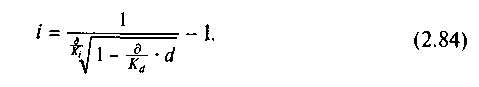
Эквивалентность сложных процентных и сложных учетных ставок. Уравнение эквивалентности для определения эквивалентных сложных процентных и сложных учетных ставок имеет вид

Отсюда получаем:

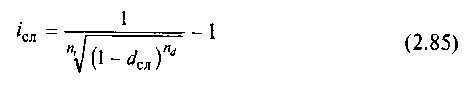
или

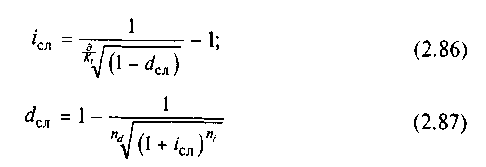
или

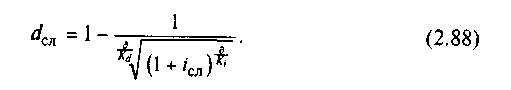
Эквивалентность эффективной и номинальной ставок сложных процентов. Рассмотрим, какое соотношение существует между номинальной и соответствующей ей эффективной годовой процентной ставкой.

Исходя из определений эффективной процентной ставки и номинальной процентной ставок, составим уравнение эквивалентности:

Отсюда получим:

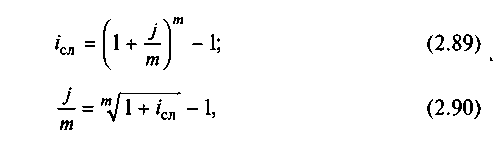
где j/m — релятивная процентная ставка.

Номинальную ставку рассчитаем по формуле

Отметим, что замена в договоре номинальной ставки j при условии, что она начисляется т раз в год, на эффективную i не изменяет финансовых результатов.

ПРИМЕР 13. Облигация достоинством 100 тыс. руб. выпущена на 5 лет при номинальной ставке 50%. Определите:

1) наращенную стоимость облигации в конце срока займа, если наращение процентов производится раз в год, по полугодиям, поквартально. Проанализируйте доходность вариантов наращения с позиций держателя и эмитента облигации;

2) эффективные процентные ставки по вариантам начисления;

3) наращенные стоимости облигации по эффективным процентным ставкам по вариантам начисления.

Решение. 1. Наращенные стоимости облигации по процентной ставке по вариантам равны:

а) при ежегодном начислении процентов

S₁ = 100 (1 + 0,5)⁵ = 100 ∙ 7,594 = 759,4 тыс. руб.;

б) при полугодовом начислении процентов

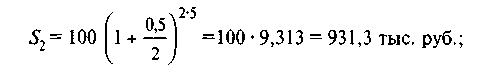
в) при квартальном начислении процентов

2. Эффективные процентные ставки по вариантам начисления равны:

а) при ежегодном начислении процентов

i_l = 0,5, или 50% годовых;

б) при полугодовом начислении процентов

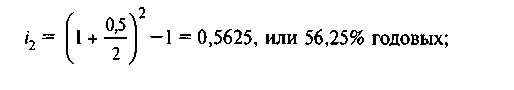
в) при квартальном начислении процентов

3. Наращенные стоимости облигации по эффективным процентным ставкам равны:

а) при ежегодном начислении процентов

S₁ = 100 (1 + 0,5)⁵ = 759,4 тыс. руб.;

б) при полугодовом начислении процентов

S₂ = 100 (1 + 0,5625)⁵ = 100 ∙ 9,313 = 931,3 тыс. руб.;

в) при квартальном начислении процентов

S₃ = 100 (1 + 0,6018)⁵ = 100 ∙ 10,545 = 1054,5 тыс. руб.

Вывод. Для кредиторов (держателей облигаций) выгоднее наращение стоимости по процентной ставке с квартальным начислением процентов, а для заемщика (эмитента облигации) — выгоднее по годовой процентной ставке.

ПРИМЕР 14. Банк принимает срочные вклады на 3 месяца с выплатой дохода за срок в размере 15%.

Определите эффективную годовую ставку процентов при вложении средств на 9 месяцев с переоформлением вклада и начислением процентов через каждые три месяца.

Решение. 1. Рассчитаем годовую номинальную процентную ставку: так как 15% — это релятивная ставка процентов (за 3 месяца), то номинальная ставка будет равна 15% ∙ т = 15% ∙ 4 = 60%, где т — количество раз начислений в год (т — 4).

2. Рассчитаем годовую эффективную ставку:

Отсюда

3. Эффективную ставку при вложении средств на 9 месяцев (³/₄ года) определяем по следующей формуле:

Ответ. Эффективная ставка процентов при вложении средств на 9 месяцев составит 69,5%.

Введем в пример 14 дополнительное условие: пусть величина вклада составит 100 тыс. руб. и рассчитаем эффективные и номинальные процентные ставки через каждые 3 месяца.

Решение.

Рассчитаем, например, наращенную сумму по номинальной (а) и эффективной (б) процентным ставкам через 9 месяцев после вложения средств. Сравним результаты расчетов:

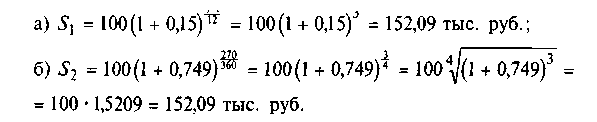
Ответ. Наращенная сумма составит 152,09 тыс. руб.