2.3.4. Расчеты в условиях инфляции

При использовании учетной ставки соотношение между суммой, которая должна быть возвращена (S), и суммой, получаемой заемщиком, можно записать в виде

где d_r — учетная ставка, обеспечивающая реальную доходность.

Погашаемая сумма в условиях инфляции, как было показано в п. 2.1.2, определяется по формуле

Подставляя эту формулу в (2.60), получаем

С другой стороны, величину S(τ) можно записать как

где d(τ) — учетная ставка, компенсирующая потери от инфляции.

Приравнивая (2.61) и (2.62), получаем

Из этого уравнения можем получить формулу для определения значения учетной ставки, компенсирующей потери от инфляции:

Замечание. Как указывалось в п. 2.1.2, формулы с использованием индекса инфляции за весь срок операции являются общими для любых сроков ссуды (меньше года, равный году или больше года). Так, если срок операции не более года (п < 1), то получим

Для срока операции, равного году (п = 1), получим

ПРИМЕР 9. Ссуда выдается 12 марта по простой учетной ставке, равной 12%. Заемщик должен 25 декабря возвратить 2 млн руб.

Определите при годовом уровне инфляции 40% для точного числа дней ссуды и К = 366:

а) учетную ставку, компенсирующую потери от инфляции;

б) выдаваемую сумму;

в) величину дисконта.

Решение. 1. Определим учетную ставку с учетом инфляции:

2. Рассчитаем выдаваемую заемщику сумму:

3. Дисконт составит

Ответ. Учетная ставка с учетом инфляции составит 39,57%; сумма, выданная заемщику, — 1,379 млн руб., доход банка — 0,621 млн руб.

2.4. Финансовая эквивалентность

2.4.1. Финансовая эквивалентность платежей

В банковской практике нередко возникают случаи, когда необходимо заменить одно финансовое обязательство другим (например, с более отдаленным сроком платежа) или объединить несколько обязательств в одно (консолидировать платежи). В таких условиях возникает вопрос о принципе, согласно которому должны проводиться изменения условий соглашения. Подобным принципом является финансовая эквивалентность обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменений условий платежей. Эквивалентными считают платежи, которые, будучи приведенными к одному и тому же моменту времени, окажутся равными. Принцип финансовой эквивалентности позволяет решать задачи по изменению условий сделок — объединению нескольких платежей в один, замене одного количества платежей другим, изменению сроков платежей, их размеров и т.д.

Общий метод решения подобных задач заключается в разработке так называемого уравнения эквивалентности, в котором сумма платежей, предусмотренных старым обязательством и приведенных к какому-либо моменту времени, приравнена к сумме платежа по новому обязательству, также приведенному к этому моменту времени.

Объединение нескольких платежей в один. Сумму объединенного платежа можно записать как

где S_oj — сумма j-го платежа, приведенного к моменту времени n_о: S_oj= S_j ∙ K_nj, где K_nj — коэффициент приведения.

Рассмотрим следующие случаи:

1. n_o > n_j,

где n_o — срок объединенного платежа; n_j — срок j-го платежа.

Коэффициент приведения будет представлять собой множитель наращения и рассчитываться по формуле

где t_j = n_q — n_j = ; д_о — дата объединенного платежа; д_j — дата j-го платежа.

2. n_o < n_j

Коэффициент приведения будет представлять собой коэффициент дисконтирования, определяемый по формуле

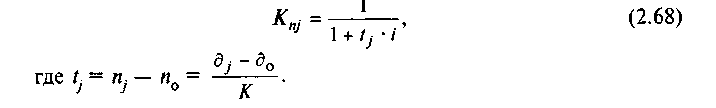
3. n_o = n_j.

Коэффициент приведения равен 1.

ПРИМЕР 10. Объединяются 4 платежа с суммами 20, 15, 10 и 25 тыс. руб. со сроками платежей 31.03, 15.05, 15.07 и 30.09. Срок объединения платежа 15.08 при простой ставке процентов 7% годовых и К = 365.

Необходимо рассчитать сумму объединенного платежа.

Решение. 1. Рассчитаем число дней от срока первоначального платежа до объединенного:

д_o – д₁ = 136 (дней) (n_o > n₁);

д_o – д₂ = 91 (день) (n_o > n₂);

д_o – д₃ = 30 (дней) (n_o > n₂);

д₄ – д₁ = 45 (дней) (n_o > n₄).

2. Рассчитаем значения коэффициентов приведения:

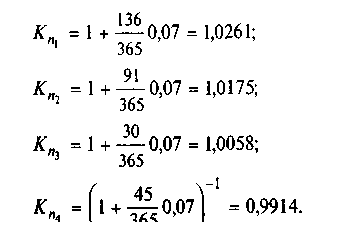
3. Сумма объединенного платежа будет равна

S_o = 20 ∙ 1,0261 + 15 ∙ 1,0175 + 10 ∙ 1,0058 + 25 ∙ 0,9914 = 70,628 тыс. руб.

Ответ. Сумма объединенного платежа составит 70,628 тыс. руб.

Замена одного количества платежей на другое. Если количество платежей по новым условиям больше одного, необходимо записать более общее уравнение эквивалентности, в котором сумма платежей по старым условиям, приведенных по заданной процентной ставке и к заданной дате приведения, приравнивается к сумме платежей по новым условиям, приведенных по той же процентной ставке и той же дате приведения.

Уравнение имеет вид

где S_а(ст) (а= 1, 2, ..., N_ct) — суммы платежей по старым условиям; К_па(ст) — коэффициенты приведения платежей по старым условиям и заданной дате приведения; S_b(н) (b = 1, 2, ..., N_н) — суммы платежей по новым условиям; К_nb,_(н) — коэффициенты приведения платежей по новым условиям к той же заданной дате приведения.

В качестве неизвестной величины, характеризующей новые условия платежей при заданных прочих условиях, целесообразно принять сумму последнего платежа.

Представим уравнение (2.69) в следующем виде:

где S_N(н) — сумма последнего платежа; К_nN(н) — коэффициент приведения последнего платежа к заданной дате приведения.

Из выражения (2.70) имеем

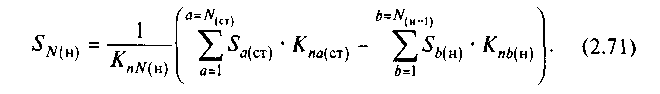
В частном случае одного объединенного платежа выражение (2.71) сводится к (2.70).