2.3.3. Коммерческое дисконтирование

Необходимость определения дисконта возникает в различных финансовых операциях, например при учете векселей и других краткосрочных обязательств. Дисконтирование векселя означает его покупку у владельца до наступления срока оплаты векселя по цене, меньшей той суммы, которая должна быть выплачена по нему в конце срока. Дисконтирование векселя является, как правило, формой кредитования банком векселедержателя путем досрочной выплаты ему обозначенной в векселе суммы за минусом определенных процентов. Часто эта операция называется учетом векселя. При учете векселя банк применяет не математический, а банковский или коммерческий учет. Согласно этому методу проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока возвращения ссуды. Применительно к учету векселя это означает, что проценты начисляются на сумму, которую должен выплатить должник в конце срока погашения векселя. Сумма, которую покупатель выплачивает векселедержателю при досрочном учете векселя, называется дисконтированной величиной векселя. Она ниже номинала векселя на процентный платеж, вычисленный со дня дисконтирования до дня погашения векселя. Этот процентный платеж называется дисконтом. Ставка, по которой начисляются проценты, отличается от ставки процентов i. Ее называют учетной или дисконтной ставкой и обозначают символом d.

Дисконтирование по простой учетной ставке. Годовая учетная ставка находится по формуле

где D — сумма процентных денег (дисконт); S — сумма, которая должна быть возвращена; n = /К — срок от даты учета до даты погашения векселя, лет; — число дней от даты учета до даты погашения векселя; К — временная база (см. разд. 2.1.1).

Отсюда

D = S ∙ n ∙ d;

где (1 — п ∙ d) — дисконтный множитель.

Следует иметь в виду, что из этой суммы банк может удержать и комиссионные за проведение операции (обычно они пропорциональны выкупной цене обязательства).

Формула наращения, в основу которой положена учетная ставка, имеет вид

где 1/1 — n ∙ d — множитель наращения.

Из формулы (2.54) становится очевидным следующее свойство простых учетных ставок: при п > 1/d величина Р станет отрицательной.

Операция дисконтирования по учетной ставке может совмещаться с операцией начисления процентов (например, при учете платежного обязательства, предусматривающего начисление процентов на указанную в нем сумму). В этом случае наращенная сумма по обязательствам с учетом процентов составит

где Р_o — первоначальная сумма обязательства; n_o — срок начисления процентов по обязательству; i_o — ставка процентов.

Подставляя (2.55) в (2.53), получаем выражение для суммы, выплачиваемой при учете такого платежного обязательства:

Дисконтирование по сложной учетной ставке. Рассмотрим применение сложной учетной ставки d при определении современной величины платежа. Учетная ставка представляет собой ставку процентов, начисляемую на сумму будущего платежа S. Пусть соответствующую сумму денег удерживают при выдаче ссуды, срок выдачи некоторой суммы S равен п. Тогда современная величина за один год до окончания срока при условии, что сумма дисконта вычитается в начале каждого года, составит

Для года (п -2) получим Р_п-2 = S(l - d) - S(1 - d) d = S(1 - d)² и т.д.

Для года, отстоящего от срока платежа на п лет, имеем

где К_n=(1- d)ⁿ — дисконтный множитель. Сумма дисконта будет равна

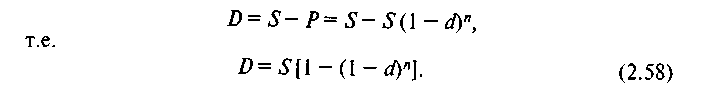
Если учет осуществляется не один, а т раз в год, то исходя из формулы (2.58) получим

где f — номинальная учетная ставка.