2.3. Дисконтирование
2.3.1. Экономическая сущность и виды дисконтирования
В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы, т.е. по заданной сумме S, которую следует уплатить через п лет, необходимо определить сумму Р (сумму на любую дату до момента уплаты S). Эта задача возникает, например, тогда, когда проценты удерживаются непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируется, а разность S — P = D называют дисконтом. Таким образом, термин «дисконтирование» в широком смысле означает определение значения Р стоимостной величины на некоторый момент времени при условии, что в будущем она составит заданную величину S. Дисконтирование позволяет учитывать в финансово-экономических расчетах фактор времени. В зависимости от вида ставки (процентной или учетной) различают два вида дисконтирования: математический и коммерческий (банковский) учет.
2.3.2. Математическое дисконтирование
Дисконтирование по простой учетной ставке. Математическое дисконтирование производится на основе процентной ставки i. К нему прибегают в тех случаях, когда по заданным S, n, i необходимо найти Р. Решив уравнение (2.1) относительно Р, получим
где Кд = 1/1 + n ∙ i — коэффициент дисконтирования или дисконтный множитель.
Дисконтный множитель является величиной, обратной множителю наращения (1 + п ∙ i). Величину Р, если она найдена по S, называют дисконтированной суммой S. Ее также называют современной (приведенной, капитализированной) величиной платежа S. Это понятие широко используется в финансовых вычислениях и экономических расчетах, так как ни одна серьезная проблема сравнения результатов финансовых операций не может быть решена без расчета сумм издержек, доходов и т.д., приведенных с помощью дисконтирования к какому-либо моменту времени.
Для различных периодов начисления и значений ставок процентов коэффициент дисконтирования будет равен
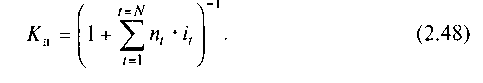
Дисконтирование по сложной процентной ставке. Из формулы по заданному значению наращенной суммы S можно определить значение первоначальной суммы Р, выдаваемой заемщику, или, иначе говоря, осуществить дисконтирование суммы S по сложной ставке процентов:
где Кд = 1/(1 + i)n = (1 + i)-n — коэффициент дисконтирования (учетный или дисконтный множитель).
Смысл дисконтной величины очевиден: Р показывает, какая сумма должна быть взята в качестве первоначальной для того, чтобы через п лет она выросла до S при ставке сложных процентов i. Таким образом, величины Р и S эквивалентны: платеж в сумме S через п лет равноценен сумме Р, выплачиваемой в настоящий момент. Коэффициент дисконтирования в этом случае может быть назван коэффициентом приведения. Современная величина платежа — одна из основных финансовых характеристик, широко используемая в самых разнообразных ситуациях. Отметим некоторые ее свойства.
Свойство 1: чем выше ставка процентов, тем сильнее дисконтирование и, следовательно, в большей степени уменьшается Р при всех прочих равных условиях.
Свойство 2: при очень больших сроках платежа современная величина последнего платежа будет очень мала.
Для разных периодов начисления и разных значений ставок процентов коэффициент дисконтирования будет равен
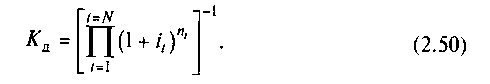
При исчислении сложных процентов т раз в году коэффициент дисконтирования будет рассчитываться следующим образом:
