2.2.2. Номинальная и эффективная ставки процентов

В современных условиях проценты, как правило, капитализируются не один, а несколько раз в год (по полугодиям, кварталам, месяцам и т.д.). Число раз начисления процентов в году обязательно фиксируется в условиях договора. Кроме того, обычно указывается и годовая ставка процентов, которая получила название номинальной (j). Номинальная ставка — основа для определения той ставки, которая действительно начисляется в каждом периоде. Если номинальная ставка равна j, то в каждом из периодов начисляются проценты по ставке j/m, где т — число раз начисления процентов в году. Например, при j = 1,8 (180% годовых) и начислении процентов по полугодиям ставка в каждом полугодии равна 0,9 (1,8 : 2), т.е. 90%, а в каждом квартале 0,45 (1,8 : 4), т.е. 45% годовых. Ставка j/m в мировой практике называется релятивной (относительной).

При декурсивном способе расчета сложных процентов наращенная сумма вычисляется по формуле

При антисипативном способе расчета сложных процентов наращенная сумма вычисляется следующим образом:

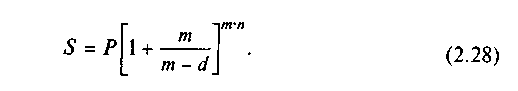
Введем понятие эффективной ставки процентов (i), под которой будем понимать ту реальную прибыль, которую получают от одной денежной единицы в целом за год. Иначе говоря, эффективная ставка эквивалентна номинальной при начислении процентов т раз в год. Она показывает, какая годовая ставка дает тот же эффект, что и т — разовое наращение в год по ставке j/m.

На практике встречаются случаи, когда общий срок ссуды измеряется не целым числом. Рассмотрим методы определения наращенной суммы для этой ситуации: а) вычисления ведутся в соответствии с формулой (2.27); б) смешанный метод.

В первом случае необходимо общую протяженность срока ссуды (n*) представить в виде суммы числа полных периодов начисления процентов (т ∙ а) и дробной части одного периода начисления (в), т.е. п* = а ∙ т + в, где а — число полных лет. Теперь наращенную сумму можно определить:

При начислении годовых процентов п*= а + в (т = 1) наращенная сумма будет равна

Рассмотренный прием исчисления процентов применяется в основном в тех случаях, когда расчет представляет некоторое промежуточное звено в общей цепи расчетов, т.е. лишь один этап в более сложных построениях (например, в страховых расчетах, анализе капитальных вложений и т.д.). На практике, если конечной целью расчета является только получение наращенной суммы S, применяют смешанный метод, суть которого состоит в том, что наращенная сумма для целого числа периодов определяется по формуле сложных процентов, а для дробной части периодов применяется формула простых процентов, т.е.

Если проценты начислены в конце года, т.е. т = 1, тогда

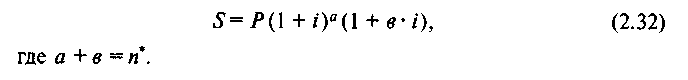
Расчеты, произведенные по формулам (2.31) и (2.32), дают несколько больший результат, чем по формулам (2.29) и (2.30). Можно легко доказать, что наибольшая разница между ними будет при в = 0,5.

2.2.3. Расчеты сложных процентов в условиях инфляции

В проведенном выше анализе, связанном с наращением процентов, не был учтен такой фактор, как инфляция. Все денежные суммы измерялись по номиналу, и реальная покупательная способность денег не принималась во внимание. Вместе с тем инфляция стала неотъемлемым элементом экономики нашей страны, и с этим нельзя не считаться при проведении долгосрочных финансовых операций. Учет инфляции необходим по крайней мере в двух случаях: при расчете наращенной суммы денег и определении реальной ставки процентов.

Если наращенная сумма денег за п лет составит величину S, а динамика цен характеризуется индексом I(τ), то реальная наращенная сумма при сохранении покупательной способности денег будет равна S* = S : I(τ).

Пусть ожидаемый уровень инфляции (темп прироста) равен τ, тогда индекс инфляции за год составит (1 + τ), а индекс покупательной способности денег будет равен (1 + τ)^-1. За п лет при сохранении предполагаемого уровня инфляции индекс покупательной способности денег будет равен (1 + τ)^-n.

1. Наращенная сумма при сохранении покупательной способности денег будет равна S* = S(1 + τ)^-n.

Отсюда

Очевидно, что если темп инфляции равен ставке процентов, по которой производится наращение, то роста реальной суммы не произойдет: наращение полностью поглощается инфляцией и, следовательно, S* = Р.

Если τ > i, то происходит «эрозия» капитала, т.е. инфляция поглощает даже часть первоначальной суммы денег и, следовательно, S* < Р.

Возникает вопрос: как же учесть в наращенной сумме денег уровень инфляции и предотвратить обесценение денег?

2. В условиях инфляции погашаемая сумма определяется по формуле

где r — ставка, обеспечивающая реальную доходность операции.

С другой стороны, S(τ) можно записать:

где i(τ) — ставка сложных процентов при выдаче ссуды с учетом инфляции.

Используя вышеприведенные формулы, получаем уравнение эквивалентности для рассматриваемой финансовой операции — выдачи ссуды по сложной ставке процентов в условиях инфляции при заданном индексе инфляции за срок ссуды:

Отсюда получаем выражения для множителя наращения с учетом инфляции:

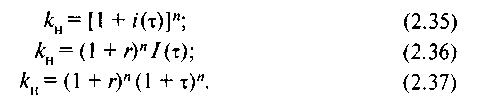
Ставка сложных процентов i(τ) при выдаче ссуды с учетом инфляции будет равна

Если п = 1, то

Рассмотрим начисление сложных процентов несколько раз в году с учетом инфляции. Наращенная сумма в конце срока ссуды, определяемая требуемой реальной доходностью операции r_j, в соответствии с формулой (2.27) будет равна

С учетом инфляции возвращаемая сумма должна составить

В то же время S(τ) может быть рассчитана следующим образом:

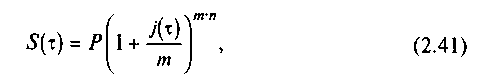
где j(τ) — номинальная ставка процентов при выдаче ссуды с учетом инфляции.

Приравняв формулы (2.40) и (2.41), получим уравнение эквивалентности для рассматриваемой финансовой операции при заданном индексе инфляции за весь срок ссуды:

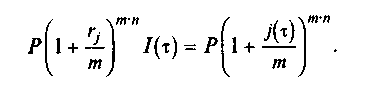
Отсюда получаем выражение для множителя наращения:

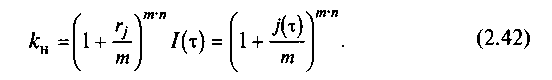
Выражение для номинальной ставки сложных процентов при их начислении т раз в году, обеспечивающей требуемую реальную доходность операции r_j при заданном индексе инфляции за срок ссуды, будет определяться следующим образом:

Отсюда релятивная ставка с учетом инфляции

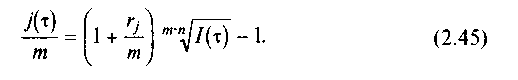
Величина наращенной суммы

Приведем пример расчетов по вышеприведенным формулам.

ПРИМЕР 8. Банком выдана ссуда 2 млн руб. Срок ссуды 2 года. Проценты начисляются поквартально по номинальной ставке 40% годовых.

Определите множитель наращения, номинальную ставку процентов с учетом инфляции и погашаемую сумму, если ожидаемый годовой уровень инфляции составляет 50%.

Решение. 1. Определяем множитель наращения по формуле (2.42):

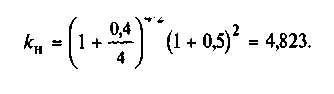
2. Определяем номинальную ставку процентов с учетом инфляции по формуле (2.44):

3. Погашаемая сумма с учетом инфляции по формуле (2.46) составит

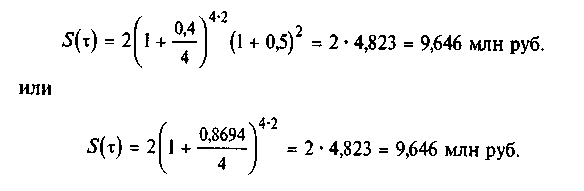
Ответы. Множитель наращения равен 4,823.

Номинальная ставка процентов с учетом инфляции составит 86,94%.

Погашаемая сумма равна 9,646 млн руб.