2.2. Сложные проценты
2.2.1. Сущность сложных процентов и их использование в банковской практике
В сложных процентах процентный платеж в каждом расчетном периоде добавляется к капиталу предыдущего периода, а в последующем периоде процентный платеж вычисляется уже на эту наращенную величину первоначального капитала. В соответствии с этим процесс роста первоначальной суммы, ее наращение происходят с ускорением. Примером увеличения капитала по сложным процентам может быть регулярное реинвестирование средств, размещенных под простые проценты на один период начисления. Способ расчета процентных платежей по сложным процентам называют начислением процента на процент.
Если процентный платеж начисляется и добавляется к величине капитала в конце каждого года, говорят, что капитализация (начисление процентного платежа) является годовой и обозначается Ра — per anum. Если процентный платеж начисляется и добавляется к величине капитала каждые шесть месяцев, то это называется полугодовой капитализацией и обозначается Ps — per semestre. Начисление сложных процентов и их капитализация каждые три месяца обозначаются Pq — per quatrure, а каждый месяц Рт — per mensem.
Существует два способа начисления сложных процентов: антисипативный (предварительный) и декурсивный (последующий). Если процентный платеж начисляется в начале каждого расчетного периода — это антисипативное начисление процентов. Декурсивное начисление процентного платежа производится, если процентный платеж начисляется и добавляется к капиталу в конце каждого расчетного периода. Именно декурсивное начисление процентов наиболее распространено в мировой практике.
В расчетах применяют так называемые дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т.д.). В некоторых случаях (в доказательствах и расчетах, связанных с непрерывными процессами, в общих теоретических построениях, а иногда и на практике) возникает необходимость в применении непрерывных процентов. В этом случае проценты начисляются за бесконечно малые промежутки времени.
Декурсивный расчет сложных процентов.
УСЛОВИЕ 1. Приведем формулу для определения наращенной суммы при условии, что проценты начисляются и капитализируются один раз в год (годовые проценты). В конце n-го года наращенная сумма составит
где (1 + i) — сложный декурсивный коэффициент; (1 + i)n — множитель наращения.
Так как в финансовых вычислениях конечным результатом является денежная сумма, то можно сказать, что экономический смысл сложного декурсивного коэффициента заключается в том, что он равен стоимости одной денежной единицы, увеличенной на процентный платеж в конце одного расчетного периода при ставке сложных процентов i. Множитель наращения показывает конечную стоимость одной денежной единицы, вложенной под сложные проценты декурсивно.
УСЛОВИЕ 2. Если срок ссуды в годах п не является целым числом, то множитель наращения может быть определен двумя способами. При первом способе используется формула (2.22) с соответствующим показателем, при втором способе (смешанный метод) множитель наращения может быть определен по формуле
где п = п (а) + пb; п (а) — целое число лет; пb — оставшаяся дробная часть года.
С точки зрения сущности начисления процентов смешанный метод является точным, а первый — приближенным, дающим меньшую величину множителя наращения.
УСЛОВИЕ 3. Предположим, что уровень ставки сложных процентов изменяется в течение срока ссуды.
Если в течение срока ссуды будет N периодов начисления, то наращенная сумма в конечном итоге составит
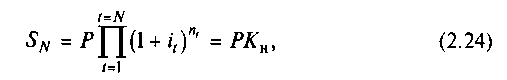
где Кн — множитель наращения.
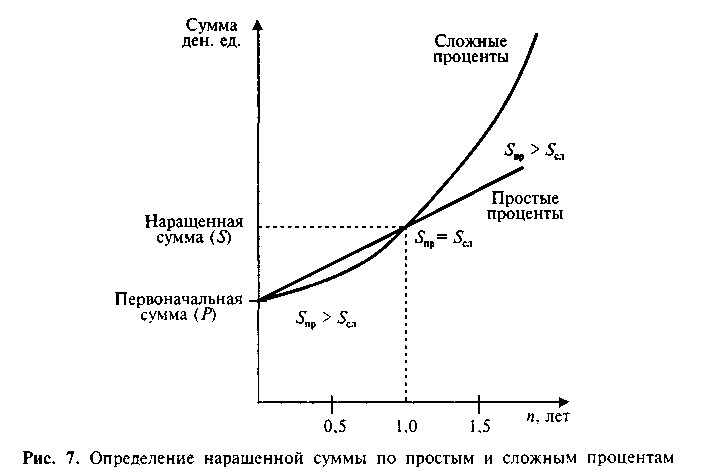
Рассмотрим графическую иллюстрацию роста вклада по простым и сложным процентам и проведем сравнительный анализ (рис. 7).
Сопоставление результатов наращения сумм по простым и сложным процентам позволяет сделать важные в практическом отношении выводы (рис. 7):
если п > 1, то (1 + n ∙ i) < (1 + i)n, отсюда Sпр< Sсл;
если п = 1, то (1 + п ∙ i) = (1 + i)n, отсюда Sпр = Sсл;
если n < 1, то (1 + п ∙ i) > (1 + i)n, отсюда Sпр > Sсл.
В практике довольно часто возникает потребность исчисления уровня годовой процентной ставки, которая обеспечивает в рамках заданного периода времени равнозначность наращенных стоимостей. Этот критерий нормы доходности должен служить экономисту в качестве инструмента оценки того или иного хозяйственного решения в сравнении с другими способами размещения средств в деловой оборот. Поясним сказанное на примере.
ПРИМЕР 6. Промышленно-финансовая компания Российской продовольственной биржи объявила в 1993 г. о привлечении свободных денежных средств населения и юридических лиц на следующих условиях:
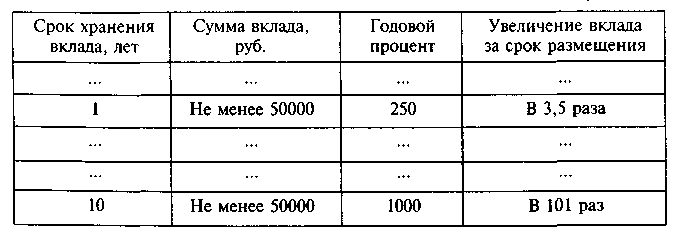
Не усложняя данную ситуацию возможным финансовым риском от данной операции, ответим на вопрос: что выгоднее с точки зрения уровня доходности — размещать временно свободные денежные средства сроком на один год или на 10 лет?
Решение. Чтобы ответить на поставленный вопрос, рассчитаем годовую процентную ставку, используя формулу (2.22). Получим, что годовая процентная ставка при 10-летнем сроке размещения вклада соответствует
При годовом размещении эта ставка составит 250% (см. таблицу). Как видим, норма доходности от годового вложения средств в несколько раз эффективнее разового вложения на 10-летний срок, а с учетом инфляции долгосрочное размещение средств вообще сомнительно.
Результаты расчетов позволяют экономисту более обоснованно судить о целесообразности совершения хозяйственных операций с точки зрения сохранения финансового капитала и требуемой нормы его наращения.
Антисипативный расчет сложных процентов. Рассмотрим, на какую сумму возрастет первоначальный капитал Р через п лет при учетной ставке d (d < 1), если вычисление сложных процентов производится антисипативным методом. Этот метод обычно применяется в условиях высокой инфляции.
Представим сумму капитала Р в начале расчетного периода как разницу суммы S1 в конце расчетного периода и процентного платежа на сумму S1, вычисленного антисипативно:
где d — учетная ставка.
Отсюда S1 =.
Формула для расчета величины капитала в конце n-го года примет вид
Тогда Sn = Р ∙ Кнn, где Кн = 1/1 - d — сложный антисипативный коэффициент; Кнп — коэффициент наращивания при антисипативном вычислении сложных процентов.
Коэффициент наращивания позволяет определить конечную сумму одной денежной единицы в конце n-го периода при учетной ставке d для антисипативного метода расчета сложных процентов.
Приведем пример, иллюстрирующий, что при декурсивном и антисипативном методах определения сложных процентов получаются различные результаты.
ПРИМЕР 7. Первоначальный капитал Р, равный 2 млн руб., вложен на 4 года под 60% годовых.
Найдите доход от вложения денег при расчете сложных процентов декурсивным и антисипативным методами.
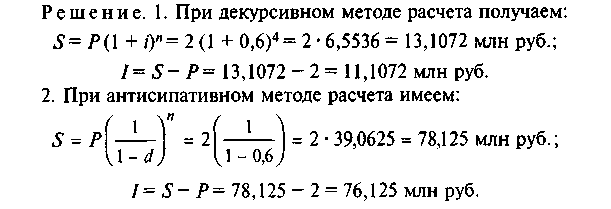
Вывод. При антисипативном расчете получается больший доход, чем при декурсивном. Поэтому антисипативный способ расчета выгодно использовать при вложении денег, если в стране высокая инфляция. При нормально действующей экономике обычно пользуются декурсивным способом расчета процентов.