2.1.2. Расчеты простых процентов в условиях инфляции
При начислении процентов может быть учтена инфляция — снижение покупательной способности денег. Инфляцию характеризуют два показателя: уровень инфляции и индекс инфляции.
Уровень инфляции показывает, на сколько процентов изменяются цены за некоторый период времени.
Индекс инфляции показывает, во сколько раз выросли цены за период времени.
Уровень инфляции и индекс инфляции за один и тот же период связаны соотношением
где I(τ) — индекс инфляции; τ — уровень инфляции.
Ясно, что покупательная способность наращенной суммы с учетом инфляции S(τ) должна быть равна покупательной способности суммы S при отсутствии инфляции. Поэтому можно записать S(τ) = S + ΔS, где ΔS — сумма, которая должна быть добавлена к сумме S для сохранения ее покупательной способности. При этом τ = ΔS/S.
Рассмотрим случай, когда ссуда в условиях инфляции выдается в начале года с последующим погашением в конце года. Предположим, что планируется реальная доходность ссудной операции в виде простой ставки процентов (r). Наращенная сумма S за год (n = 1) будет определяться S = Р(1 + r), где r — реальная доходность ссудной операции.
Предположим, что задан годовой уровень инфляции (τгод).
Тогда ΔSгод = S ∙ τгод.
Отсюда
В условиях инфляции погашаемая сумма S(τ) за год должна составить
С другой стороны, величину S(τ) можно представить в виде
где i(τ) — простая ставка процентов при выдаче ссуды, учитывающая инфляцию; Kn(τ) — множитель наращения в условиях инфляции.
В результате имеем
Коэффициент наращения по реальной доходности операции будет равен
Отсюда получаем выражение для простой ставки процентов, учитывающей в рассматриваемом случае ожидаемый уровень инфляции. Оно носит название эффект Фишера:
На практике часто используют получаемое по формуле (2.11) приближенное значение ставки процентов по кредиту в условиях инфляции при заданных значениях реальной годовой ставки процентов и годового уровня инфляции:
Погашаемая сумма с учетом инфляции при n < 1 будет равна
Другой способ расчета процентов по краткосрочным ссудам (при n < 1) в условиях инфляции заключается в задании уровня инфляции за интервал, меньший срока ссуды (например, месяц). В этом случае индекс инфляции за срок, включающий несколько таких периодов (например, квартал, полугодие, год), определяется по формуле
где τ1 — уровень инфляции за период t; N — количество периодов в течение рассматриваемого срока.
Исходя из (2.14) получим: S(τ) = Sr ∙ I(τ), т.е.
Отсюда
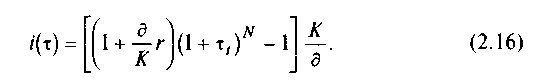
Если срок ссуды равен году и задан годовой уровень инфляции, то выражение (2.16) сводится к выражению (2.11).
ПРИМЕР 3. Определите годовой уровень инфляции, ставку процентов при выдаче ссуды с учетом уровня инфляции 20% в месяц и погашаемую сумму для ссуды в размере 10 млн руб., выдаваемой на три месяца при требуемой реальной доходности операции 8% годовых.
Решение. 1. Рассчитаем индекс инфляции к концу года:
I(τ) = (1 + 0,2)12 = 8,916 (891,6%).
2. Годовой уровень инфляции равен
τ = 8,916 – 1 = 7,916 (791,6%).
3. Индекс инфляции за три месяца равен
I(τ) = (1 + 0,2)3 = 1,728 (172,8%).
4. Ставка процентов при выдаче ссуды с учетом инфляции составит
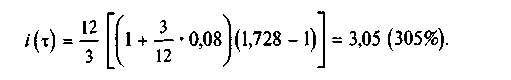
5. Погашаемая сумма будет равна
Покупательная способность этой суммы составит 10,2 млн руб. (17,625/1,728).
Ответ. Погашаемая сумма равна 17,625 млн руб. при ставке процентов с учетом инфляции 305 % годовых.
Рассмотрим случай, когда при заданном годовом уровне инфляции ссуда выдается на срок более года (п > 1).
Если п — целое число, то
где I(τ) = (1 + τгод)n.
Отсюда
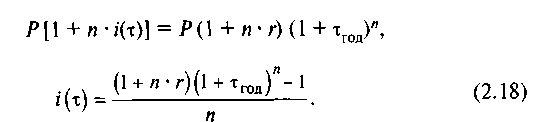
Формулу (2.18) можно рассматривать как общий случай расчета простой процентной ставки с учетом инфляции.
ПРИМЕР 4. Ссуда в 20 млн руб. выдана на 2,5 года. Прогнозируемый годовой уровень инфляции в течение этого срока оценивается в 90%.
Определите ставку процентов при выдаче ссуды с учетом инфляции и погашаемую сумму, если требуемая реальная доходность операции составляет 10% годовых.
Решение. 1. Ставку процентов при выдаче ссуды с учетом инфляции рассчитаем по формуле (2.18):
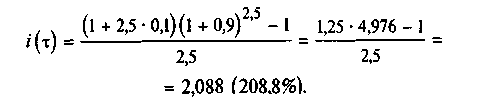
2. Погашаемая сумма с учетом инфляции составит
Покупательная способность этой суммы равна 25 млн руб. (124,4 : (1 + 0,9)2,5).
Ответ. Погашаемая сумма через 2,5 года составит с учетом инфляции 124,4 млн руб.
Предположим, что при выдаче ссуды задается ожидаемый индекс инфляции за весь срок ссуды. Тогда
Отсюда множитель наращения равен
Из выражения (2.19) получим формулу для расчета простой ставки процентов при выдаче ссуды, если задан индекс инфляции за весь срок ссуды:
Формула (2.20) универсальна для расчета простых процентов с учетом инфляции с любыми сроками ссуды, и при ее использовании не требуется предположения о том, каким образом будет изменяться уровень инфляции в течение срока ссуды.
Ясно, что инфляция влияет на реальную (с точки зрения покупательной способности) доходность вкладных и кредитных операций. Реальное значение суммы с начисленными процентами за некоторый срок, приведенное к моменту предоставления денег в долг, S* = S / I(τ).
При использовании простых ставок процентов и одном периоде их начисления
ПРИМЕР 5. Банк принимает депозиты на полгода по ставке 90% годовых.
Определите реальные результаты вкладной операции для вклада размером 500 тыс. руб. при месячном уровне инфляции 8%.
Решение. 1. Рассчитаем сумму вклада с процентами на полгода
S = 500 (1 + 0,5 ∙ 0,9) = 725 тыс. руб.
2. Индекс инфляции за весь срок хранения депозита (6 месяцев) составит
I(τ) = (1 + 0,08)6 = 1,59 (159%).
3. Сумма вклада с начисленными процентами по своей покупательной способности с учетом инфляции будет соответствовать сумме
S* = 725 : 1,59 = 455,975 тыс. руб.
Ответ. С учетом покупательной способности рубля наращенная сумма составит 455,975 тыс. руб.