Глава 2. Наращение и дисконтирование

2.1. Простые проценты

2.1.1. Сущность простых процентов и их использование в банковской практике

Простые проценты — это метод расчета дохода кредитора от предоставления денег в долг заемщику. Сущность простых процентов заключается в том, что они начисляются на одну и ту же величину капитала в течение всего срока ссуды.

Рассмотрим построение формулы для начисления простых процентов. Для этого выясним, какие показатели влияют на изменение суммы процентных денег.

Сумма процентных денег зависит от суммы долга (Р); срока его выплаты, выражаемого в годах (п); процентной ставки (О, характеризующей интенсивность начисления процентов. Процентная ставка показывает, сколько денежных единиц должен заплатить заемщик за пользование одной денежной единицей капитала в определенном периоде времени (за год).

Начисленные проценты за один период равны Р ∙ i, а за п периодов — Р ∙ п ∙ i. Сумма, образовавшаяся к концу года, состоит из двух элементов — первоначальной суммы долга и процентов: S = Р +I, или

где п — срок долга в годах; i — годовая ставка простых процентов (десятичная дробь).

Отношение наращенной суммы к первоначальной сумме долга S : P = k_h называют множителем (коэффициентом) наращения: k_н = (1 + ni).

Выражение (2.1) представляет собой формулу для определения наращенной суммы при использовании простой годовой ставки процентов. Приведенная формула применяется как для расчета суммы вклада с процентами, так и для определения суммы кредита с процентами при его погашении единовременным платежом. Простые проценты используются также при помещении валютных средств на краткосрочные депозиты.

Если срок, на который берутся деньги в долг, задан в днях, то наращенная сумма будет равна

где д — продолжительность периода в днях; К — расчетное количество дней в году.

Величину К называют временной базой для расчета процентов. Временная база может браться равной фактической продолжительности года — 365 или 366 дней (точные проценты). За базу измерения часто берут год, условно состоящий из 360 дней (12 месяцев по 30 дней). В этом случае вычисляют обыкновенные проценты или коммерческие проценты. При одинаковом числе дней ссуды соотношение между точными и обыкновенными процентами будет следующим:

где K_t и K_o — количество дней для расчета соответственно точных процентов и обыкновенных процентов.

Отсюда имеем взаимосвязь в расчетах по точным и приближенным процентам:

Количество дней в каждом месяце в течение срока долга также можно брать точно или приближенно (30 дней).

В мировой банковской практике используют следующие три варианта расчетов:

1. Обыкновенные проценты с приближенным числом дней ссуды. Этот вариант обычно используют в Германии, Дании, Швеции и называют германской практикой.

2. Обыкновенные проценты с точным числом дней ссуды. Этот вариант распространен во Франции, Бельгии, Испании, Швейцарии и называется французской практикой.

3. Точный процент с точным числом дней ссуды. Этот вариант применяется в Англии, Португалии, США и называется английской практикой.

В России применялись все три варианта расчетов.

Французская практика расчетов, как правило, использовалась в операциях коммерческих банков; германская — когда не требовалось большой точности расчетов; английская обычно применялась ЦБ при расчетах с банками-контрагентами.

В зависимости от использования конкретной практики начисления процентов их сумма будет различаться. С точки зрения банка предпочтительным является вариант с большим значением процентных денег, т.е. французская практика, а с точки зрения заемщика — вариант германской практики, т.е. с меньшим значением процентных денег.

Согласно Положению ЦБ о порядке начисления процентов [8, п. 3.9] в настоящее время коммерческим банком рекомендовано при начислении суммы процентов по привлеченным и размещенным денежным средствам в расчет принимать фактическое количество календарных дней, на которые привлечены или размещены денежные средства, а за базу брать действительное число календарных дней в году.

В банковской практике при расчете процентов используются понятия «процентное число» и «процентный ключ» (дивизор). Рассмотрим эти понятия. В формуле для вычисления процентов числитель и знаменатель разделим на i (в процентах) и получим

где Р ∙ /100 — процентное число; D = K/i — процентный ключ или дивизор.

Понятно, что процентный платеж, вычисляемый с использованием дивизора 365/i, будет меньше, чем процентный платеж, получаемый при использовании дивизора 360/i. Поэтому при обслуживании конкретного заемщика используется только один из дивизоров. В составе общей финансовой отчетности коммерческих банков записка 5 «Наращенные проценты» дает анализ процентов, накопленных на дату отчетности по ссудам и депозитам. Каждый раз, когда сумма на счете изменяется, рассчитывается процентное число за прошедший период, в течение которого сумма на счете оставалась неизменной. Для определения суммы процентов за весь срок их начисления все процентные числа складываются и их сумма делится на постоянный делитель-дивизор.

Рассмотрим пример.

ПРИМЕР 2. При открытии сберегательного счета по ставке 80% годовых 20 мая на счет была положена сумма 10 млн руб. Затем 5 июля на счет была добавлена сумма 15 млн руб., 10 сентября со счета снята сумма 20 млн руб., а 20 ноября счет был закрыт.

Определите сумму начисленных процентов, используя при этом германскую практику.

Решение. 1. Рассчитаем срок хранения сумм:

10 млн руб. - 45 дней [12 {май} + 30 + 5 {июль} - 2];

10 + 15 = 25 млн руб. - 65 дней [27 {июль} + 30+10 {сентябрь} - 2];

25 - 20 = 5 млн руб. - 69 дней [21 {сентябрь} + 30 + 20 {ноябрь} - 2].

2. Рассчитаем сумму процентных чисел

3. Постоянный делитель будет равен 360 : 80 = 4,5.

4. Рассчитаем сумму начисленных процентов

24,2 : 4,5 = 5,38 млн руб.

Ответ. Сумма начисленных процентов составит 5,38 млн руб.

Данная методика по своей сути является последовательным применением формулы процентных денег на каждом интервале постоянства суммы на счете, т.е. I = I₁ + I₂ + I₃:

Ответ. Сумма начисленных процентов составит 5,38 млн руб.

Если ставка процентов на разных интервалах начисления в течение срока будет изменяться, то наращенную сумму можно определить по формуле

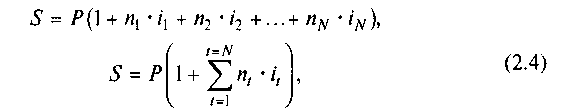
где N — количество интервалов начисления процентов; n_t — длительность t-гo интервала начисления; i_t — простая ставка процентов на t-м интервале начисления.

Множитель наращения в данном случае будет иметь вид